С) Бесконечность определенного количества 7 глава

Это заставляет нас поразмыслить о различии [в мнениях] относительно того, в чем состоит определенность какой-нибудь фигуры, а именно эта определенность или такова, какова в данном случае высота фигуры, или она внешняя граница. Поскольку она дана как внешняя граница, допускают, что непрерывность фигуры, так сказать, следует равенству или отношению границы; например, равенство совпадающих фигур основывается на совпадении ограничивающих их линий. Но в параллелограммах с одинаковой высотой и основанием лишь последняя определенность есть внешняя граница. Высота, а не вообще параллельность, на которой основано второе главное определение фигур, их отношение, прибавляет к внешней границе второй принцип определения. Эвклидово доказательство равенства параллелограммов, имеющих одинаковую высоту и основание, приводит их к треугольникам, к внешне ограниченным непрерывным; в доказательстве же Кавальери, и прежде всего в доказательстве пропорциональности параллелограммов, граница есть вообще определенность величины, как таковая, обнаруживающаяся в любой паре линий, проведенных в обеих фигурах на одинаковом расстоянии. Эти равные или находящиеся в равном отношении к основанию линии, взятые совокупно, дают находящиеся в равном отношении фигуры. Представление об агрегате линий противоречит непрерывности фигуры; но рассмотрение линий полностью исчерпывает ту определенность, о которой идет речь. Кавальери часто отвечает на то возражение, будто представление о неделимых приводит к тому, что должны быть сравнимы между собой бесконечные по численности линии или поверхности (Geom., lib. II, prop. I, schol.); он проводит правильное различие, говоря, что он сравнивает между собой не их численность, которую мы не знаем, правильнее сказать, не их численность, которая, как мы отметили выше, есть пустое вспомогательное представление, а лишь величину, т. е. количественную определенность, как таковую, которая равна занимаемому этими линиями пространству; так как последнее заключено в границах, то и эта его величина заключена в тех же границах; непрерывное, говорит он, есть не что иное, как сами неделимые; если бы оно было нечто находящееся вне их, то оно было бы несравнимо; но было бы нелепо сказать, что ограниченные непрерывные несравнимы между собой.

Как видим, Кавальери хочет провести различие между тем, что́ принадлежит к внешнему существованию непрерывного, и тем, в чем состоит его определенность и что́ единственно и следует выделять для сравнения и в целях получения теорем о нем. Категорий, которыми он пользуется при этом, говоря, что непрерывное сложено из неделимых или состоит из них и т. п., конечно, недостаточно, так как при этом прибегают также к созерцанию непрерывного или, как мы сказали выше, к его внешнему существованию; вместо того чтобы сказать, что «непрерывное есть не что иное, как сами неделимые», было бы правильнее и, стало быть, само собой ясно сказать, что определенность величины непрерывного есть не что иное, как определенность величины самих неделимых. — Кавальери не придает никакого значения сомнительному выводу, что существуют-де бо́льшие и меньшие бесконечные, выводу, делаемому схоластикой из представления, что неделимые составляют непрерывное, и он определенно выражает далее (Geom., lib. VII, praef.) уверенность в том, что его способ доказательства вовсе не заставляет иметь представление о непрерывном как о сложенном из неделимых; непрерывные лишь следуют пропорции неделимых. — Кавальери говорит, что он берет агрегаты неделимых не с той стороны, с какой они кажутся подпадающими под определение бесконечности из-за бесконечного множества линий или плоскостей, а поскольку они имеют в самих себе некоторый определенный характер и природу ограниченности. Но чтобы устранить и этот камень преткновения, он в специально для этого добавленной седьмой книге не жалеет труда доказать основные теоремы своей геометрии таким способом, который остается свободным от примеси бесконечности. — Этот способ сводит доказательства к упомянутой выше обычной форме наложения фигур, т. е., как мы уже отметили, к представлению об определенности как о внешней пространственной границе.

Относительно этой формы наложения можно прежде всего сделать еще и то замечание, что она вообще есть, так сказать, ребяческая помощь чувственному созерцанию. В элементарных теоремах о треугольниках представляют их два рядом, и, поскольку в каждом из них из шести частей те или иные три принимаются равными по величине соответствующим трем частям другого треугольника, показывается, что такие треугольники совпадают между собой, т. е. что каждый из них имеет и остальные три части равными по величине частям другого, так как они ввиду равенства трех первых частей совпадают друг с другом. Формулируя это более абстрактно, можно сказать, что именно в силу равенства каждой пары соответствующих друг другу частей обоих треугольников имеется только один треугольник; в последнем три части принимаются за уже определенные, из чего следует определенность также и трех остальных частей. Таким образом, показывается, что в трех частях определенность завершена; стало быть, для определенности, как таковой, три остальные части оказываются излишеством — излишеством чувственного существования, т. е. созерцания непрерывности. Высказанная в такой форме качественная определенность выступает здесь в [своем] отличии от того, что́ предлежит в созерцании, от целого как некоторого непрерывного внутри себя; совпадение мешает осознать это различие.

Вместе с параллельными линиями и в параллелограммах появляется, как мы отметили, новое обстоятельство: отчасти равенство одних только углов, отчасти же высота фигур, от которой отличны внешние границы последних, стороны параллелограммов. При этом возникает сомнение, следует ли в этих фигурах — кроме определенности одной стороны, основания, которое дано как внешняя граница, — принимать в качестве другой определенности другую внешнюю границу (а именно другую сторону параллелограмма) или высоту? Если даны две такие фигуры, имеющие одинаковое основание и высоту, причем одна из них прямоугольная, а другая с очень острыми углами (и, стало быть, с очень тупыми противолежащими углами), то последняя фигура легко может показаться созерцанию большей, чем первая, поскольку созерцание берет предлежащую большую сторону ее как определяющую и поскольку оно по способу представления Кавальери сравнивает площади по тому или иному множеству параллельных линий, которыми они могут быть пересечены; [согласно этому способу представления], бо́льшую сторону [остроугольного параллелограмма] можно было бы рассматривать как возможность большего количества линий, чем у вертикальной стороны прямоугольника. Однако такое представление не служит возражением против метода Кавальери; ибо множество параллельных линий, представляемое в этих двух параллелограммах для сравнения, предполагает в то же время одинаковость их расстояний друг от друга или от основания, из чего следует, что другим определяющим моментом служит высота, а не другая сторона параллелограмма. Но далее это меняется, когда мы сравниваем между собой два параллелограмма, имеющие одинаковые основание и высоту, но лежащие не в одной плоскости и образующие с третьей плоскостью разные углы; здесь параллельные сечения, возникающие, когда представляют себе их пересеченными третьей плоскостью, движущейся параллельно себе самой, уже не одинаково удалены одно от другого, и эти две плоскости неравны между собой. Кавальери обращает особое внимание на это различие, которое он определяет как различие между transitus rectus и transitus obliquus [123] неделимых (как в Exercit. I n. XII сл., так уже в Geometr. I, II), и этим он устраняет поверхностное недоразумение, могущее возникнуть с этой стороны. Я припоминаю, что Барроу в своем упомянутом выше сочинении (Lect. geom., II, р. 21), хотя также пользуется методом неделимых, но, нарушая его чистоту, соединяет его с перешедшим от него к его ученику Ньютону и к другим современным ему математикам, в том числе и к Лейбницу, признанием возможности приравнять криволинейный треугольник, как, например, так называемый характеристический, прямолинейному, поскольку оба бесконечно, т. е. очень малы, — я припоминаю, что Барроу приводит подобное возражение Такэ [124], остроумного геометра того времени, также пользовавшегося новыми методами. Имеющееся у последнего сомнение касается также вопроса о том, какую линию — а именно при вычислении конических и сферических поверхностей — следует принимать за основной момент определения для рассуждения, основанного на применении дискретного. Такэ возражает против метода неделимых, утверждая, что при вычислении поверхности прямоугольного конуса по этому атомистическому методу треугольник, [получаемый при продольном рассечении] конуса, изображается составленным из прямых, параллельных основанию линий, перпендикулярных к оси и представляющих собой в то же время радиусы тех кругов, из которых состоит поверхность конуса. Если же эта поверхность определяется как сумма окружностей, а эта сумма определяется из численности их радиусов, т. е. из длины оси конуса, из его высоты, то получаемый результат противоречит сформулированной и доказанной еще Архимедом истине. В ответ на это возражение Барроу показывает, что для определения поверхности конуса не его ось, а сторона треугольника, [получаемого при продольном рассечении] конуса, должна быть принята за ту линию, вращение которой образует эту поверхность и которая, а не ось, должна поэтому считаться определенностью величины для множества окружностей.

Подобного рода возражения или сомнения имеют своим источником единственно лишь обыденное неопределенное представление, согласно которому линия состоит из бесконечного множества точек, плоскость — из бесконечного множества линий, и т. д.; этим представлением затушевывается сущностная определенность величины линий или плоскостей. — Целью настоящих примечаний было раскрыть те утвердительные определения, которые при различном применении бесконечно малых в математике остаются, так сказать, на заднем плане, и освободить их от того тумана, в который их закутывает эта считающаяся чисто отрицательной категория. В бесконечном ряде, как, например, в Архимедовом измерении круга, «бесконечность» означает только то, что закон дальнейшего определения известен, но так называемое конечное, т. е. арифметическое выражение, не дано, сведе́ние дуги к прямой линии не осуществимо; эта несоизмеримость есть их качественное различие. Качественное различие дискретного и непрерывного вообще содержит также и отрицательное определение, ввиду которого они выступают как несоизмеримые и которое влечет за собой бесконечное в том смысле, что непрерывное, долженствующее быть принятым за дискретное, по своей непрерывной определенности не должно уже иметь определенное количество. Непрерывное, которое арифметически должно быть принято за произведение, тем самым полагается в самом себе дискретным, а именно разлагается на те элементы, которые составляют его множители; в этих множителях заключается определенность его величины; и именно потому, что они суть эти множители или элементы, они имеют низшее измерение, а поскольку появляется степенна́я определенность, имеют более низкую степень, чем та величина, элементами или множителями которой они служат. Арифметически это различие обнаруживается как чисто количественное различие, как различие корня и степени или какой-нибудь другой степенно́й определенности. 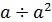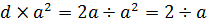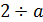Но если это выражение имеет в виду лишь количественное, как таковое, например или , или для закона падения тел , то оно дает лишь ничего не говорящие отношения , , ; в противоположность своему чисто количественному определению члены отношения должны были быть удержаны врозь своим различным качественным значением, как, например, 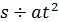, где величина выражена как некоторое качество, как функция величины некоторого другого качества. При этом сознание имеет перед собой лишь количественную определенность, над которой легко производятся подобающие действия, и можно спокойно умножать величину одной линии на величину другой; но в результате умножения этих самых величин получается также качественное изменение — переход линии в плоскость, поскольку появляется некоторое отрицательное определение; оно и вызывает ту трудность, которую можно устранить, если уразуметь особенность этого определения и простую суть дела; но введением бесконечного, от которого ожидается ее устранение, эта трудность скорее только запутывается еще больше и оставляется совершенно непреодоленной.