Глоссарий по теме
Неравномерное движение – если тело за одинаковые промежутки времени проходит разные расстояния - то такое движение называется неравномерным.
Скорость – это векторная величина равная отношению пути, пройденного телом за некоторый период времени, к величине этого периода времени.
Средняя скорость при неравномерном движении – отношение вектора перемещения тела к промежутку времени, за который это перемещение произошло.
Мгновенная скорость – это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:
Ускорение – это физическая величина, численно равная изменению скорости за единицу времени. Равноускоренное движение – скорость тела за равные промежутки времени изменяется одинаково, то есть движется с постоянным ускорением.
Открытые электронные ресурсы:
2. https://kvant.mccme.ru/1983/10/p33.htm
Основное содержание урока.
Неравномерное движение тел может быть не только прямолинейным, но и криволинейным.
Полное описание неравномерного движения тела, возможно при знании его положения и скорости в каждый момент времени. Скорость точки в данный момент времени называется мгновенной скоростью (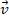
)
Любая точка в движении при определённой скорости перемещается из начального положения в конечное. Эту скорость называют средней скоростью перемещения точки.
Определяется по формуле:
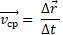
Кроме мгновенной и средней скоростей перемещения для описания движения чаще пользуются средней путевой скоростью.
Эта средняя скорость определяется отношением пути к промежутку времени, за которое этот путь пройден:
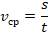
Скорости тел при движении меняются по модулю, по направлению или же одновременно как по модулю, так и по направлению.
Изменения скорости теле могут происходить как быстро, так и медленно.
Ускорением тела называется предел отношения изменения скорости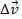 
к промежутку
Времени ∆t, в течении которого это изменение призошло, при стремлении ∆t к нулю.
Ускорение обозначается буквой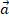 
.
Определяется по формуле:
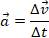
Единица ускорения – м/с2
Выясним зависимости точки от времени при её движении с постоянным ускорением. Для этого воспользуемся формулой:
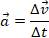
Пусть 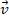о – скорость точки в начальный момент времени to, а 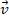– в некоторый момент времени t, тогда:
∆t = to,
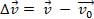
и формула для ускорения примет вид:
Если начальный момент времени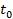 
принять равным нулю, то получим:
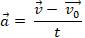
Отсюда получим формулу для определения скорости точки в любой момент времени при её движении с постоянным ускорением:
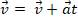
Вектору уравнению соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:
𝑣х = 𝑣ох + 𝒂х t;
𝑣у = 𝑣оу = 𝒂уt.
Мы научились, таким образом, находить скорость материальной точки при движении с постоянным ускорением.
Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.
Допустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость XOY. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты х и у. Обозначим через хо и уо координаты в начальный момент времени tо = 0, а через х и у координаты времени.
Тогда за время ∆t = t – to = t изменения координат будут равны
∆ х = х – хо и ∆ у = у – уо
Отсюда:
х = хо + ∆ х,
у = уо + ∆ у
График зависимости v(t)
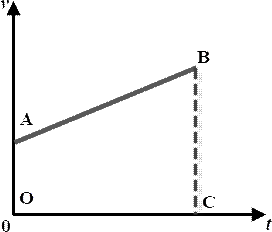
По формуле для площади трапеции имеем:
Учитывая, что 𝑣 ₓ = 𝑣ₒₓ + 𝒂ₓt, получаем формулу:
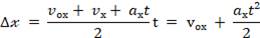
В обычных условиях задачи даются значения (модули) скоростей и ускорений:
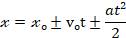
При движении точки в плоскости ХОY двум уравнениям соответствует одно векторное уравнение:
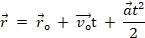
Разбор тренировочных заданий
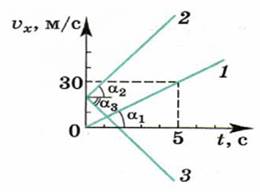
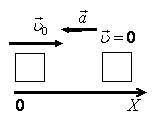
1. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?
Направление движения определяем по направлению скорости, изменение скорости – по направлению ускорения и скорости.
Решение:
Тело 1 движется вправо; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 2 движется вправо; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
Тело 3 движется влево; направления ускорения и скорости совпадают, следовательно, скорость его увеличивается.
Тело 4 движется влево; ускорение направлено в противоположную сторону скорости, следовательно, скорость его уменьшается.
2. Электропоезд тормозит с ускорением 0,40 м/с2. Определите, за какое время он остановится, если тормозной путь равен 50 м.
Решение:
При прямолинейном движении путь электропоезда равен перемещению s = ∆r. Так как электропоезд останавливается, то 𝑣 = 0 Скорость уменьшается, поэтому ускорение направлено против движения.
Используются величины:
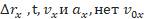
Поэтому воспользуемся уравнением^
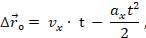
Тогда:
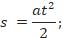
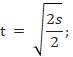
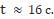
Ответ: t ≈ 16 c.
д/з §8 законспектировать решить на стр33 А1-А4; Ответы и решения отправить на почту matheмаtuka@yandex.соm