Исходные данные для выполнения РГР

ГЛАВА 7. КРУЧЕНИЕ

Общие понятия

Кручением называется такой вид деформации стержня, при котором во всех его поперечных сечениях действует только одно внутреннее усилие - крутящий момент. Крутящий момент принято обозначать . Крутящий момент действует в плоскости поперечного сечения стержня вокруг его оси. Деформация кручения возникает в стержне под действием скручивающих моментов, действующих в плоскостях, перпендикулярных оси стержня.

Для крутящего момента примем следующее правило знаков (рис.7): при направлении против хода часовой стрелки, глядя со стороны внешней нормали к поперечному сечению, крутящий момент считается положительным, при направлении по ходу часовой стрелки - отрицательным.

 

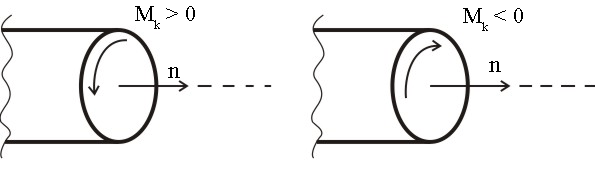
Рис. 7. Правило знаков крутящего момента .

При кручении стержня в его поперечных сечениях действуют только касательные напряжения τ. Например, рассмотрим распределение касательных напряжений в случае, когда поперечное сечение стержня является круглым с диаметром (Рис.8.). В этом случае касательное напряжение в точке сечения направлено перпендикулярно диаметру, проходящему через эту точку, в сторону крутящего момента и по величине прямо пропорционально расстоянию от данной точки до центра .

Рис.8. Распределение касательных напряжений τ в круглом поперечном сечении стержня при кручении.

, (7)

Здесь - геометрическая характеристика круглого сечения, называемая полярным моментом инерции.

В рассматриваемом сечении максимальное касательное напряжение достигается в наиболее удаленных от центра точках сечения с расстоянием и вычисляется по формуле:

 

(8)

Где называется полярным моментом сопротивления круглого сечения стержня.

Полярный момент инерции и полярный момент сопротивления допускается вычислить по приближенным формулам

 

; (9)

Касательное напряжение определяется по модулю и его величина не зависит от направления крутящего момента. В качестве измерения касательного напряжения обычно используется мегапаскаль (МПа).

При кручении стержня предполагается, что его длина остается неизменной и его поперечные сечения остаются плоскими (гипотеза плоских сечений Бернулли).

Пусть стержень (или участок стержня) длиной с круглым поперечным сечением кручения с постоянным крутящим моментом . Тогда угол закручивания (рад) такого стержня (угол поворота одного граничного сечения относительно другого граничного сечения) прямо пропорционально крутящему моменту(закон Гука при кручении)

 

, (10)

Где (МПа) является характеристикой механических свойств материала и называется модулем сдвига или модулем касательной упругости. Формула (10) справедлива в ограниченном диапазоне крутящего момента .

Условие прочности стержня при кручении формулируется следующим образом: максимальное касательное напряжение не должно превышать допускаемое касательное напряжение :

 

. (11)

Пример выполнения РГР

“Расчет стержня на прочность и жесткость при кручении”

Стальной стержень (Рис.8.9) состоит из трех участков одинаковой длины и с круглыми сечениямидиаметрами и . Стержень испытывает деформацию кручения под действием внешних моментов , , . Модуль сдвига ; Допускаемое касательное напряжение .

Построить эпюры крутящего момента , максимального касательного напряжения и угла поворота поперечных сечений ; проверить стержень на условие прочности.

Рис.8.9 Исходная схема стержня.

Решение.

Разобьем стержень на три участка нагружения, границами которых являются сечения, в которых действуют скручивающие моменты М; и изменяются диаметры поперечных сечений. Пронумеруем эти участки слева направо, т.е. в положительном направлении оси стержня (Рис 8.10 а). На этих участках крутящие моменты будут постоянными.

Для определения крутящего момента будем использовать левые отсеченные части стержня. Поэтому из уравнения равновесия моментов относительно оси ( принимаем за положительное направление против хода часовой стрелки, глядя с положительного направления оси )

,

 

Предварительно найдем реакцию 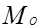в заделке

 

.

Знак минус у найденного момента означает, что он направлен в противоположном направлении, показанном на рис.8.4 а) и по модулю равен .

Определенный крутящий момент всегда следует вводить как положительный, т.е. направленный против хода часовой стрелки. На участке 1 сделаем сечение с координатой и воспользуемся левой отсеченной частью стержня. Из уравнения равновесия моментов относительно оси (Рис.8.11 а)

находим

 

 

Аналогичным образом определяем крутящий момент на остальных участках.

Участок 2: (Рис. 8.11 б).

 

 

Участок 3: (Рис.8. 16 в).

 

 

.

 

По полученным результатам расчетов строим эпюру крутящего момента (Рис.8.10 б).

Вычисляем полярные моменты сопротивления круглых сечений с заданными диаметрами и по формулам:

 

 

 

Затем определяем максимальное касательное напряжение на данных участках:

 

 

Эпюра максимальных касательных напряжений изображена на рис.8.10 в).

Условие прочности () выполняется на всех трех участках.

 

Вычисляем полярные моменты инерции круглых сечений с заданными диаметрами и по формулам ():

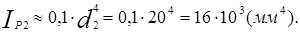
Рис.8.10 Эпюры крутящего момента , максимального касательного напряжения и угла поворота поперечных сечений .

а)

б)

в)

Рис.8.11. Определение крутящего момента методом сечений.

Углы закручивания участков стержня определяем по формуле ():

 

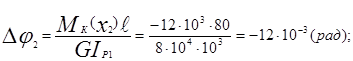
Тогда углы закручивания граничных сечений стержня равны

(сечение в заделке закреплено);

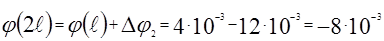(рад);

(рад);

(рад).

 

Промежуточные сечения стержня на каждом участке поворачивают согласно линейной зависимости между поворотами соответствующих граничных сечений. Эпюра углов поворота всех поперечных сечений стержня изображена на рис.8.10 г).

 

Исходные данные для выполнения РГР

Постановка задачи полностью соответствует той, которая сформулирована в п.7.2.

 

Исходные схемы приведены в таблице 2.

Таблица 2.

№	Исходная схема
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.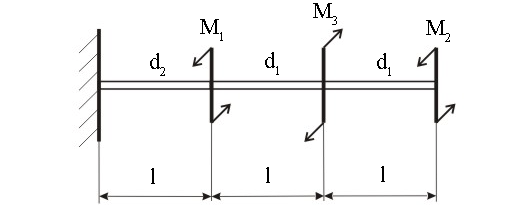
13.
14.
15.
16.
17.
18.
19.
20.
22.
23.
24.
25.