
Ситуация: Онлайновый турнир по системе «садись и играй» (sit-and-go). Призовые выплаты осуществляются игрокам, занявшим три первых места в стандартном соотношении: 50% первому, 30% второму и 20% третьему. В игре осталось четверо. По сравнению с предыдущей Задачей блайнды и анте увеличились.
Ваша рука:??
Игра до вас: Как и в Задаче № 37, игрок A делает ход олл-ин, а игрок В на позиции малого блайнда сбрасывает. Вы полагаете, что у игрока A такой же диапазон рук для хода олл-ин, как и ранее: любая пара, любая рука с тузом, король-валет или выше, как одномастные, так и разномастные, и дама-валет, одномастные и разномастные.
Вопрос 38: Какое из следующих утверждений верно?
A. Сбросить все руки
B. Делать колл только с AA
C. Делать колл только с AA и KK
D. Делать колл с AA, KK, QQ и AK одномастными или разномастными
E. Делать колл с руками от AA до TT и AK и AQ, одномастными или разномастными
F. Делать колл с руками от AA до 88 и от AK до AJ, одномастными или разномастными
Решение Задачи № 38
Ситуация такая же, как и в предыдущей задаче, за исключением того, что размер блайндов и анте вырос. Блайнды теперь равны $200 и $400, а анте $25, поэтому начальный пот равен $700. Ваше значением М теперь чуть выше 7, тогда как игроки с мелкими стеками имеют М около 2 и 3.
Изменение размера блайндов, как оказалось, почти никак не влияет на вашу стратегию. Вариант C все еще верный ответ — колл только с AA и KK. Запишите 3 очка за этот ответ и 1 очко за любой из вариантов B или D. Ситуация для вас ухудшилась, потому что значение M стало ниже, но положение игроков с мелкими стеками ухудшилось так же, как и ваше. В результате вы чуть-чуть больше склоняетесь к продолжению игры, но не настолько, чтобы изменить список рук для колла против лузового игрока.
|
|
Если мы заставим игрока А повысить его требования к силе рук для хода олл-ин, как в прошлой задаче, так чтобы подходящими руками стали восьмерки или выше, туз-десятка или выше и король-дама или выше, тогда вы сможете делать коллы как с королями, так и с тузами. Появление королей в этом списке показывает, что при более низком значении М вы чуть сильнее склоняетесь к продолжению игры, но вам все еще нужна рука-«монстр» страшной силы.
Задача № 39
Игра в «пузыре»:
Турнир за одним столом — 3

Ситуация: О нлайновый турнир типа «сит-эн-гоу» (sit-and-go). Призовые в турнире присуждаются трем игрокам занявшим первые места в стандартном соотношении: 50% за первое место, 30% за второе и 20% за третье. В игре осталось четыре игрока. Теперь вы не лидер по количеству фишек, наоборот, у вас один из самых мелких стеков.
Ваша рука:??
Игра до вас: Как и в Задаче № 37, игрок А делает ставку олл-ин, а игрок В и игрок на позиции алого блайнда сбрасывают. Вы считаете, что игрок А использует такой же диапазон рук для хода олл-ин, как и раньше: любая пара, любая рука с тузом, король-валет или выше, как одномастные, так и разномастные, и дама-валет, одномастные и разномастные.
Вопрос 39: Какое из следующих утверждений верно?
A. Делать колл только с AA
B. Делать колл только с AA и KK
C. Делать колл только с АА, КК и QQ
D. Делать колл с руками от АА до JJ и с AK одномастными
E. Делать колл с руками от AA до TT и AK и AQ, одномастными или разномастными
F. Делать колл с руками от AA до 88 и от AK до AJ, одномастными или разномастными
G. Делать колл с руками от AA до 44 и от AK до A9, одномастными или разномастными плюс KQ
|
|
Решение Задачи № 39
Мы возвращаемся к структуре блайндов из Задачи № 37 ($100 и $200), но теперь у нас изменился размер стеков. На этот раз у вас один из самых мелких стеков за столом равный $2 000, и вам приходится отвечать на ставку олл-ин от одного из соперников, имеющего $5 000. Как и ранее, вы считаете, что у него относительно лузовые требования к силе рук для олл-ин. Что вам нужно для того, чтобы уравнять его ставку?
Вы могли подумать, что со таким стеком, который по размеру стоит на предпоследнем месте, и со значением М ниже 7, ваши требования к силе рук для колла должны быть весьма лузовыми. Многие игроки выбрали бы вариант G, который действительно оставлял бы их фаворитами в большинстве случаев.
Но лучший ответ- вариант D: "Делать колл с руками от АА до JJ и с AK одномастными!" Хотя ваши требования к силе рук и не такие тайтовые, как в ситуации, когда у вас был большой стек, они все еще остаются крайне тайтовыми. Вы будете делать колл только с лучшими 2% своих рук. Занимая третье место за столом по количеству фишек, вы не можете рисковать вероятностью вылететь из «пузыря», если у вас нет никакой иной руки, кроме «монстра» страшной силы, даже в том случае, когда вы знаете, что ваш противник готов атаковать со многими посредственными руками. Запишите 3 очка за выбор варианта D и 1 очко либо за вариант C либо за вариант Е.
В качестве отступления заметим, что ели бы игрок А использовал более тайтовый список рук для олл-ин, как в двух предыдущих задачах (восьмерки или выше плюс туз-десятка или выше плюс король-дама одномастные или разномастные), тогда ваши требования для колла стали бы еще более высокими: пара дам или выше. Это немного более лузово, чем в двух предыдущих задачах, но все равно очень-очень тайтово.
|
|
Вывод: Значение М равное 7, хотя и является низким, все равно дает вам время подождать, пока не придет более сильная рука, с которой можно рискнуть всеми своими фишками.
Хотя аргументы в пользу тайтовой игры в ситуации пузыря кажутся в целом рациональными, особенно, когда у вас крупный стек (как в двух предыдущих примерах), этот пример, вероятно, обеспокоит некоторых наших читателей. В конце концов, здесь вы идете на третьем месте с относительно мелким стеком, а мы тем не менее выступаем за крайне тайтовый подход. Чтобы более четко проиллюстрировать, что на самом деле имеет место, мы собираемся показать вам подробный анализ того, что в действительности происходит с вашим финансовым положением в турнире, когда вы делаете колл в подобных ситуациях.
Предупреждение: Следующая часть решения задачи содержит столько математических расчетов, что некоторые читатели могут почувствовать себя неуютно. Если в вашем случае это так, просто пропускайте остальную часть решения этой задачи и переходите к Задаче № 40. Но если вам на самом деле любопытно и вы хотите узнать, что же в действительности происходит, продолжайте читать.
Мы начнем с расчета активов каждого игрока, выраженных в наличных деньгах, на разных этапах розыгрыша руки, а затем рассмотрим изменения прибыли для каждого возможного исхода. В целях упрощения анализа, мы предположим, что игроки борются за призовой фонд в сумме $1 000 с призами $500 за первое место, $300 за второе и $200 за третье. Игрок, занявший четвертое место, не получает, конечно же, ничего.
Расчет материальных активов не так прост, но его можно выполнить с помощью системного подхода. Мы начнем с расчета активов для четырех игроков на тот момент, когда розыгрыш руки еще не начался. Обозначим четырех игроков буквами от A до D, у которых будут стеки следующих размеров:
· Игрок A: $5 000
· Игрок B: $5 000
· Игрок C: $2 000
· Игрок D: $1 500
Поскольку активы игрока зависят от точного значения вероятности того, закончит ли игрок турнир на первом, на втором или на третьем месте, то нам придется сперва рассчитать эти вероятности. Этот требует построения следующей таблицы вероятностей:
Таблица I: Вероятность окончания турнира на определенном месте, рассчитанная на момент начала розыгрыша руки
| Игрок | стек | первое | второе | третье | четверное |
| A | $5000 | 0,37 | 0,329 | 0,244 | 0,057 |
| B | $5000 | 0,37 | 0,329 | 0,244 | 0,057 |
| C | $2000 | 0,148 | 0,193 | 0,279 | 0,38 |
| D | $1500 | 0,111 | 0,15 | 0,232 | 0,507 |
Каждое значение в соответствующей ячейке этой таблицы показывает вероятность окончания турнира на определенном месте для данного игрока в данный момент. Например, игрок А является одним из двух лидеров по количеству фишек со стеком $5 000. У него 37% шансов на то, чтобы занять первое место, 32,9% шансов на то, чтобы занять второе место, 24,4% шансов занять третье и всего 5,7% шансов оказаться на последнем месте без приза. (Конечно, мы предполагаем, что у всех игроков одинаковый уровень мастерства.)
Перед тем, как объяснить, как мы рассчитали эти значения, заметим, что эта матрица подчиняется всем условиям здравого смысла, которые только можно предположить. Игроки A и B, имеющие одинаковые стеки, имеют и равные вероятности закончить турнир на каждом из четырех соответствующих мест. Игрок D с самым мелким стеком имеет наименьшую вероятность закончить турнир на первом месте и самую большую вероятность закончить четвертым. Сумме каждой колонки равна 1,0 (на каждом конкретном месте должен оказаться один из игроков) и сумма каждой строки также равна 1,0 (ведь каждый из игроков должен оказаться на каком-то месте).
Итак, откуда взяты эти вероятности? Давайте начнем с колонки, в которой содержатся вероятности занятия первого места каждым из игроков, поскольку эти вероятности рассчитать проще всего. Вероятность каждого игрока закончить на первом месте является простым соотношением его количества фишек к общему числу фишек в игре.
Например, игрок A имеет 37% фишек:
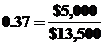
Для игрока D это соотношение равно 11,1%:

Расчет вероятностей для второго места становится немного сложнее. Например, чтобы рассчитать шансы игрока А занять второе место, нам придется сделать три отдельных вычисления:
1. Во-первых, предположим, что игрок B заканчивает турнир на первом месте. (Из колонки с вероятностями для первого места мы знаем, что вероятность этого события составляет 37,0 %.) Шансы игрока А занять второе место равны соотношению суммы его фишек ($5 000) к общему количеству фишек у трех остальных игроков A, C и D. Их сумму фишек равна $8500. Поэтому шансы игрока А закончить турнир вторым с учетом того, что В финиширует первым, равны 58,8%:

Вероятность одновременного возникновения этих двух событий (B финиширует на первом месте, затем A финиширует на втором) равна 0,370 умножить на 0,588, то есть 0,218.
2. Во-вторых, выполним то же самое вычисление для того случая, когда на первом месте финиширует игрок С. Если C занимает в турнире первое место (14,8% случаев), тогда у трех других игроков в сумме будет фишек на $11 500, поэтому вероятность того, что А заканчивает на втором месте в данный момент равна 43,5%:

Вероятность одновременного возникновения этих двух событий (игрок C первый, A второй) равна 0,148 умножить на 0,435, или 0,064.
3. Наконец, рассчитаем вероятность того, что игрок D закончит турнир на первом месте, а игрок A – на втором. Ответ будет 0,046.
Общая вероятность того, что игрок А заканчивает турнир на втором месте, равна сумме этих вероятностей или 0,329:
0,329 = 0,218 + 0,064 + 0,046
Использование табличных вычислений, как можно догадаться, значительно упрощает расчеты.
Для расчета вероятностей для третьего места используется такая же идея, но при этом требуется еще больше вычислений. Существует 12 различных вероятных комбинаций того, какие именно двое из четырех игроков могут оказаться на первых двух местах (игрок A первый, B второй, затем A первый, C второй, и так далее до сочетаний D первый, а С второй.) При каждой из этих 12 ситуаций двум игрокам остается бороться за третье место, и каждый имеет шансы, пропорциональные сумме его фишек, деленной на общую сумму фишек, которые имеются у двух остальных игроков. Каждый из 12 случаев вносит свое значение вероятности того, что один из двух оставшихся игроков займет третье место. Сложите все значения для всех 12 случаев и вы получите вероятности для третьего места.
Вероятности четвертого места не требуется рассчитывать напрямую, поскольку все вероятности для данного игрока в суме равны 1,000.
Как только вероятности для данной ситуации готовы, вы можете использовать их для получения той информации, которая нас действительно интересует, а именно, активы каждого игрока на основе полученных значений. Эти активы будут следующими:
Таблица II: Активы для каждого игрока до начала розыгрыша руки, с учетом того, что призы распределяются данным образом ($500 за первое место, $300 за второе и $200 за третье)
| Игрок A | $332,63 |
| Игрок B | $332,63 |
| Игрок C | $187,71 |
| Игрок D | $147,02 |
Расчет этих сумм весьма прост. Просто помножьте вероятность для данного игрока закончить турнир на данном месте на сумму приза для данного места, и сложите полученное значение для каждого игрока. Для игрока A расчет будет выглядеть следующим образом:
$332,63 - (0,370)($500) + (0,329)($300) + (0,244)($200)
Некоторые игроки пытаются рассчитать эти суммы активов приблизительно, умножая общую сумму призового фонда на долю фишек каждого игрока на данный момент. Для игрока А такое приближение даст $370, это не так далеко от действительной цифры, полученной нами. Однако, использование этого метода дает значения активов, которые слишком завышены для лидеров по количеству фишек на данный момент и слишком занижены для тех, кто отстает.
Используя этот метод, мы можем рассчитать активы для каждого возможного исхода розыгрыша данной руки и сравнить их. Давайте сделаем это и рассчитаем результаты трех возможных исходов руки в Задаче № 39:
1. Игрок A идет олл-ин и игрок С сбрасывает
2. Игрок A идет олл-ин; игрок C уравнивает и выигрывает
3. Игрок A идет олл-ин; игрок C уравнивает и проигрывает
Не утомляя вас подробностями расчетов, приводим итоговые значения активов для всех трех исходов:
Таблица III: Активы каждого игрока после завершения розыгрыша руки с одним из трех возможных исходов для Задачи № 39.
| Игрок | Колонка 1: A идет олл-ин, C сбрасывает | Колонка 2: A идет олл-ин, C уравнивает и выигрывает | Колонка 3: A идет олл-ин, C уравнивает и выигрывает |
| A | $343, 97 | $242, 41 | $394,32 |
| B | $330, 75 | $324, 56 | $353,69 |
| C | $175, 35 | $293, 97 | $0,00 |
| D | $149, 93 | $139, 06 | $251,99 |
Пока все идет хорошо. Для начала посмотрим на первую колонку, в которой игрок C сбрасывает в ответ на ставку ход олл-ин от игрока А. Если игрок С сбросит, он теряет все активы по сравнению с положением на момент начала розыгрыша руки, тогда как игрок A получает некоторые дополнительные средства. Однако, изменения в активах не ограничиваются только игроками A и C, хотя только эти два игрока напрямую участвуют в розыгрыше данной руки. Игрок В немнго теряет, поскольку A теперь выходит на чистое первое место, тогда как игрок D получает небольшие дополнительные средства, поскольку его положение приближается к игроку С.
Однако, по-настоящему интересные результаты видим во второй и третьей колонках, которые суммируют то, что происходит, когда игрок С отвечает коллом и рискует всей своей турнирной судьбой. Чтобы более четко увидеть, что происходит, давайте составим новую таблицу, которая показывает изменения активов, только когда игрок С делает колл:
Таблица IV: Изменения активов для каждого игрока, когда игрок С делает колл.
| Игрок | Колонка 2 – Колонка 1 Приобретения/потери, когда С делает колл и выигрывает | Колонка 3 – Колонка 1 Приобретения/потери, когда С делает колл и проигрывает |
| A | -$101,56 | +50,35 |
| B | -$6,19 | +22,94 |
| C | +$118,62 | -$175,35 |
| D | -$10,87 | + 102,06 |
Давайте сперва посмотрим на вторую колонку. Когда C уравнивает и проигрывает, он проигрывает все свои активы размером $175,35, активны, которые он сохранил бы, сделав сброс. (Кстати, обратите внимание, куда переходит эта сумма. Относительно небольшая ее часть отходит к игроку А. Большая часть отходит к игроку D, который теперь гарантированно получает третий приз размером $200.)
Итак, сделав колл игрок C рискует суммой $175,35. Но что он ожидает получить в обмен на свой риск? Посмотрим на первую колонку. Если он выигрывает, его приобретения активов равны всего $118,62! И это узловой момент проблемы игрока С — несмотря на его непрочное положение в турнире, он все еще ожжет потерять больше, чем выиграть от противостояния со ставкой олл-ин.
Фактически отношение его потенциальных потерь к его потенциальным приобретениям равно:

это огромная разницаa 1,48-к-1, или почти ровно 3 к 2. Делая колл, он на самом деле отдает шансы сопернику, а не получает их, а чтобы оказаться в прибыльной ситуации, ему нужно быть в этой руке фаворитом в среднем в 60% случаев, когда он делает колл! Какие руки сделают его фаворитом в соотношении 60 на 40 против списка рук для хода олл-ин, который использует игрок А? Для этого годятся только ряд самых крупных пар плюс одномастные туз-король. Отсюда этот крайне тайтовый подход для колла.
Давайте сделаем еще одно наблюдение, прежде чем закончить обсуждение этой задачи. Посмотрите на соотношении риска и вознаграждения для игрока А, играющего с крупным стеком. Когда игрок С делает колл и выигрывает, игрок А крупно проигрывает, так как потеря его активов составит $101,56. Но когда игрок С делает колл и игрок А выигрывает, большая часть потерянных активов игрока С уходит на сторону! Игрок С собирает $22,94, а игрок D с мелким стеком схватит впечатляющие $102,06. Игрок А снова остается с жалкими $50,35. Отношение потерь к приобретениям для игрока А почти точно равно 2 к 1, а это значит, что игроку А нужны очень сильные руки, чтобы оправдать его ход олл-ин.
По причине необычного распределения приобретений и потерь активов игра в ситуации пузыря требует от всех участников розыгрыша в целом очень консервативной стратегии, поскольку значения М достаточно высоки. В нашем примере сумма блайндов составляла $300, поэтому значения М варьировались от 5 у игрока D и более чем 7 у игрока С до приблизительно 17 у игроков A и B. Эти значения М достаточно высоки, чтобы в игре преобладала осторожность.
Задача № 40
Игра в «пузыре»: