Проверка некоторых равенств множеств

В этом параграфе будет более подробно рассказано о том, как проверять равенства множеств. Хорошим наглядным средством для этого служат диаграммы Эйлера-Венна, на которых множества условно изображаются в виде геометрических фигур на плоскости (как правило, в виде кругов). Это даёт возможность наглядно представить себе процесс построения более сложных множеств из простых с помощью изученных в предыдущем параграфе основных операций над множествами.

Пример. Ниже представлены диаграммы Эйлера-Венна для множеств A È B, A Ç B, A \ B, B \ A, A Ç (B È C), (A Ç B) È (A Ç C):

 

 

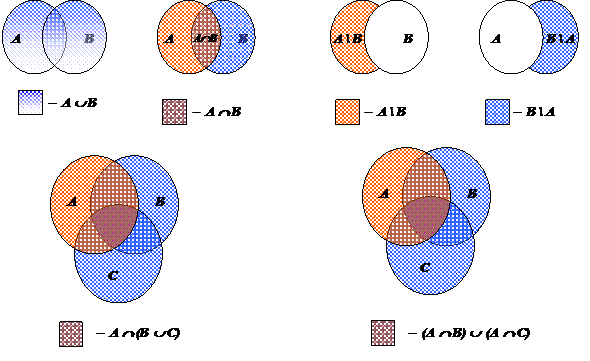
Эти диаграммы наводят на мысль, что последние два множества должны совпадать: A Ç (B È C) = (A Ç B) È (A Ç C). Однако такое зрительное восприятие не является доказательством равенства множеств, оно лишь может помочь заметить это равенство. Чтобы получить формальное доказательство равенства указанных множеств, нужно, следуя определению, доказать, что для любого x верно x Î A Ç (B È C) «x Î (A Ç B) È (A Ç C). Это можно сделать, следуя приводимому ниже общему алгоритму:

1. расписываем все отношения принадлежности в левой и правой частях доказываемой эквивалентности, следуя формальному определению операций над множествами:

x Î A Ç (B È C) º (x Î A) Ù (x Î B È C) º (x Î A) Ù (x Î B Ú x Î C),

x Î (A Ç B) È (A Ç C) º x Î (A Ç B) Ú x Î (A Ç C) º

º (x Î A Ù x Î B) Ú (x Î A Ù x Î C).

Таким образом, левая и правая части доказываемой эквивалентности записаны через элементарные высказывания вида x Î Y и их отрицания x Ï Y º º с помощью логических связок.

2. для участвующих в полученных записях элементарных высказываний введём буквенные обозначения: так, в рассматриваемом конкретном случае, обозначим a = (x Î A), b = (x Î B), c = (x Î C), сведя доказательство к проверке истинности формулы a Ù (b Ú c) «(a Ù b) Ú (a Ù c).

3. равенство множеств имеет место тогда и только тогда, когда полученная формула будет законом логики: в рассматриваемом случае это закон дистрибутивности. Следовательно, рассматриваемое равенство множеств A Ç (B È C) = (A Ç B) È (A Ç C) доказано.

В дальнейшем будут приведены другие примеры доказательств равенств множеств.

Если же на диаграммах Эйлера-Венна получаются заведомо разные рисунки множеств, то равенство множеств не выполнено, т.к. оно нарушается уже в частном случае фигур на плоскости. Например, A \ B ¹ B \ A, что видно из построенных выше диаграмм Эйлера-Венна для множеств A \ B и B \ A.

Теорема (об основных равенствах множеств). (I) Для любых множеств A, B, C справедливы следующие равенства:

(1) A = A (закон тождества),

(2) A Ç A = A (идемпотентность пересечения),

A È A = A (идемпотентность объединения),

(3) A Ç B = B Ç A (коммутативность пересечения),

A È B = B È A (коммутативность объединения),

(4) (A Ç B) Ç C = A Ç (B Ç C) (ассоциативность пересечения),

(A È B) È C = A È (B È C) (ассоциативность объединения),

(5) (A È B) Ç C = (A Ç С) È (B Ç C) (законы дистрибутивности

(A Ç B) È C = (A È С) Ç (B È C) пересечения и объединения),

(6) A \ (B \ C) = (A \ B) È (A Ç C),

(7) (A \ B) \ C = (A \ C) \ B = A \ (B È C),

(8) A = (A Ç B) È (A \ B) и (A Ç B) Ç (A \ B) = Æ,

(9) A \ (B Ç C) = (A \ B) È (A \ C),

A \ (B È C) = (A \ B) Ç (A \ C),

(10) (A Ç B) \ C = (A \ C) Ç (B \ C),

(A È B) \ C = (A \ C) È (B \ C),

(11) A \ A = Æ, A È Æ = A, A Ç Æ = Æ.

(II) Если U – универсальное множество, то для любых множеств А и В справедливы равенства:

(12) A È U = U, A Ç U = A,

(13) A Ç = Æ, A È = U,

(14) = A,

(15) = Ç , = È

(16) A Í B тогда и только тогда, когда Ê .

Доказательство. Докажем лишь некоторые равенства, оставляя остальные в качестве упражнений.

(3) A Ç B = B Ç A. Вначале строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемого равенства.

Теперь докажем формально: нужно доказать, что x Î A Ç B «xÎ B Ç A. Имеем:

xÎ A Ç B º (x Î A) Ù (x Î B), xÎ B Ç A º (x Î B) Ù (x Î A),

и обозначая а = (x Î A), b = (x Î B), приходим к формуле a Ù b «b Ù a, которая является законом логики (закон коммутативности конъюнкции).

Равенство множеств A Ç B = B Ç A доказано.

(8) A = (A Ç B) È (A \ B), ( A Ç B) Ç (A \ B) = Æ. Строим диаграмму Эйлера-Венна, которая подтверждает правдоподобность доказываемых равенств.

Теперь докажем первое равенство: нужно доказать, что x Î A «xÎ (A Ç B) È (A \ B).

x Î (A Ç B) È (A \ B) º

º (x Î A Ç B)Ú (x Î A \ B) º

º (x Î A Ù x Î B) Ú (x Î A Ù ).

Таким образом, обозначив a = (x Î A), b = (x Î B), получим формулу a «(a Ù b) Ú (a Ù ), которая является законом логики: (a Ù b)Ú (a Ù ) º a Ù (bÚ ) º a Ù 1 º a. Равенство множеств A = (A Ç B) È (A \ B) доказано.

Для доказательства второго равенства (A Ç B) Ç (A \ B) = Æ нужно лишь учесть, что по определению пустого множества, высказывание x Î Æ тождественно ложно. Таким образом, остаётся доказать, что x Î (A Ç B) Ç (A \ B) «0. Это делается по стандартной схеме:

x Î (A Ç B) Ç (A \ B) º (x Î A Ç B) Ù (x Î A \ B) º

º (x Î A Ù x Î B) Ù (x Î A Ù x Ï B) º (a Ù b) Ù (a Ù ) º a Ù b Ù a Ù º

º a Ù a Ù b Ù º a Ù 0 º 0.

Утверждение (8) доказано.

(9) A \ (B È C) = (A \ B) Ç (A \ C). Строим диаграммы Эйлера-Венна, которые подтверждают правдоподобность доказываемого равенства.

 

 

Формальное доказательство проводится стандартно: для проверки истинности формулы x Î A \ (B È C) «x Î (A \ B) Ç (A \ C) перепишем её левую и правую части, используя определения операций над множествами:

x Î A \ (B È C) º x Î A Ù º x Î A Ù º a Ù ,

x Î (A \ B) Ç (A \ C) º (x Î A \ B) Ù (x Î A \ C) º

º (x Î A Ù x Ï B) Ù (x Î A Ù x Ï C) º (a Ù ) Ù (a Ù ).

Остаётся проверить, что формула a Ù «(a Ù ) Ù (a Ù ) является законом логики. Это следует из законов ассоциативности, коммутативности, идемпотентности и законов де Моргана:

a Ù º a Ù ( Ù ) º a Ù a Ù Ù º (a Ù ) Ù (a Ù ).

Равенство A \ (B È C) = (A \ B) Ç (A \ C) доказано.

Все утверждения п. (II) теоремы можно вывести из уже доказанных равенств п. (I).

(12) A Ç U = A. В самом деле,

A = (A Ç U ) È (A \ U ) = (A Ç U ) È Æ = A È U.

Здесь использовано равенство A \ U = Æ, которое легко следует из того, что А Í U: x Î A \ U º x Î A Ù x Ï U º x Î A Ù 0 º 0 º x Î Æ.

(14) = A. Действительно,

= U \ = U \ (U \ A) = (U \ U) È (U Ç A) = Æ È A = A.

(16) Если A Í B, то x Î A ® x Î B – тождественно истинное высказывание. Докажем, что Ê , т.е. что высказывание x Î ® x Î тоже тождественно истинно. Пусть, как обычно, a = (x Î A), b = (x Î B). Тогда x Î º x Ï B º , x Î º и по закону контрапозиции получаем x Î ® x Î º ( ® ) «(a ® b) º 1, что и требовалось.

Если наоборот Ê , то по уже доказанному, Í , т.е. A Í B, что и требовалось.

Теорема доказана.

Понятие булевой алгебры

Даже беглое сравнение законов логики (см. теорему об основных законах логики) и основных равенств множеств показывает их схожесть: Любой закон логики вида A «B, где в формулах A, B участвуют лишь связки Ù, Ú, , превращается в верное равенство, если заменить « на =, а логические связки Ù, Ú, – на операции Ç, È, соответственно. В чём причина такой аналогии?

Рассмотрим следующую конструкцию. Пусть на множестве Вдля любых a, b Î В однозначно определены элементы a Ù b, a Ú b, , . Говорят, что В – булева алгебра, если выполнены следующие свойства:

ассоциативность: a Ú (b Ú c) = (a Ú b) Ú c,

a Ù (b Ù c) = (a Ù b) Ù c,

коммутативность: a Ú b = b Ú a, a Ù b = b Ù a,

поглощение: a Ù (a Ú b) = a, a Ú (a Ù b) = a,

дистрибутивность: a Ú (b Ù c) = (a Ú b) Ù (a Ú c),

a Ù (b Ú c) = (a Ù b) Ú (a Ù c),

существование 0 и 1: $ 0, 1 = Î В " x Î В x Ú 0 = x

свойства дополнения: " x Î В $ Î В .

Примеры: 1. Пусть В = {0, 1}, а операции Ù, Ú, – обычные логические связки – конъюнкция, дизъюнкция и отрицание. Ясно, что все свойства выполнены, т.е. В = {0, 1} – булева алгебра.

2. Пусть Ф – множество всех формул исчисления высказываний с точностью до равносильности. Это значит, что любые две равносильные формулы считаются равными. Это согласуется с логическим смыслом формул: важен ведь не внешний вид формулы, а принимаемые ею значения, так что отождествлять формулы с одинаковыми значениями вполне естественно. Если под операциями Ù, Ú, снова понимать обычные логические связки, то получим булеву алгебру с бесконечным числом элементов.

3. Если A – произвольное множество, то булеан В (А) является булевой

алгеброй относительно операций Ç – пересечения множеств, È – объедине-

ния множеств и – дополнения.

Удивительно, что сформулированных аксиом булевой алгебры достаточно для вывода всех других логических или теоретико-множественных законов. Докажем лишь несколько общих свойств, следующих из аксиом.

1⁰. В любой булевой алгебре ноль единственен.

Действительно, если 0₁ и 0₂ – два нуля, то (из свойства нуля) для любого x Î В верно x Ú 0₁ = x = x Ú 0₂. Поэтому 0₁ = 0₁ Ù 0₂ = 0₂ Ù 0₁ = 0₁. Здесь использовано свойство коммутативности конъюнкции.

2⁰. В любой булевой алгебре единица единственна.

Это следует из единственности нуля и формулы 1 = .

3⁰. В любой булевой алгебре " x Î В x Ù 0 = 0.

В самом деле,

0 = {поглощение} = 0 Ú (0 Ù x) = (0 Ù x) Ú 0 = 0 Ù x = x Ù 0,

что и требовалось доказать.

4⁰. В любой булевой алгебре " x, y Î В .

В самом деле, из , переходя к дополнениям и используя свойство двойного дополнения, получим .

5⁰. В любой булевой алгебре " x Î В x Ù 1 = x, x Ú 1 = 1, x Ú = 1.

Действительно, из свойства нуля и законов де Моргана получаем

, ,

1 = ,

что и требовалось доказать.

6⁰. В любой булевой алгебре

" x, y Î В x Ù ( Ú y) = x Ù y, x Ú ( Ù y) = x Ú y.

В самом деле, по дистрибутивности x Ù ( Ú y) = (x Ù ) Ú (x Ù y) = = 0 Ú (x Ù y) = x Ù y. Аналогично доказывается и второе равенство.

7⁰. В любой булевой алгебре x Ù x = x, x Ú x = x

Действительно, x = x Ù 1 = x Ù (x Ú ) = (x Ù x) Ú (x Ù ) = (x Ù x) Ú 0 = x Ù x, x Ú x = .

Таким образом, логические формулы и множества оказались двумя сторонами одной медали – их объединило понятие булевой алгебры.

Оказывается, что булеан В (А) является, основным примером булевой алгебры, что показывают следующие теоремы, приводимые без доказательства.

Теорема (о строении конечной булевой алгебры). Любая конечная булева алгебра ( В, Ù, Ú, ) изоморфна булевой алгебре ( В (А), Ç, È, ) для некоторого конечного множества А. В частности, число элементов конечной булевой алгебры является натуральной степенью числа 2.

Использованное здесь понятие изоморфизма понимается в общеалгебраическом смысле: существует взаимно однозначное отображение h: В ® В (А), сохраняющее операции, т.е.

" a, b Î В h(a Ù b) = h(a) Ç h(b), h(a Ú b) = h(a) È h(b), h() = .

В общем случае имеет место

Теорема (Стоуна). Любая булева алгебра ( В, Ù, Ú, ) изоморфна некоторой булевой подалгебре в ( В (А), Ç, È, ).

Подалгеброй булевой алгебры ( В, Ù, Ú, ) называется любое подмножество H Í В, замкнутое относительно всех выделенных операций, т.е. " f, h Î H f Ù h, f Ú h, , Î H.

На самом деле теорема Стоуна значительно сильнее, но для её полной формулировки нужны некоторые топологические понятия, которые не рассматриваются в данном курсе.

Л И Т Е Р А Т У Р А

1. Кон П. Универсальная алгебра. – М.: Мир, 1971.

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.

3. Новиков Ф.А. Дискретная математика для программистов. – СПб: ПИТЕР, 2007.

4. Сикорский Р. Булевы алгебры. – М.: Мир, 1969.