Вопрос 3. Связь алгебры высказываний с исчислением высказываний

ПОСТРОЕНИЕ ВЫВОДОВ ИЗ СОВОКУПНОСТИ ФОРМУЛ

1. Вывод формулы из совокупности формул. Правила выводимости.
2. Теорема дедукции. Доказательство некоторых законов логики.
3. Связь между алгеброй высказываний и исчислением высказываний.

Вопрос 1. Вывод формулы из совокупности формул. Правила выводимости

Пусть дана конечная совокупность (множество) формул Н = {А₁,А₂,…,А_n}.

 

О.1.1. Выводом формулы В из множества формул Н называется последовательность формул В₁,В₂,…, В_k такая, что ее каждая формула В_i (i = 1,2,…, k) является либо аксиомой, либо формулой из Н, либо получается из некоторых предыдущих формул этой последовательности по одному из правил вывода, причем В_k = В.

 

Если существует вывод формулы В из совокупности формул Н = {А₁,А₂,…,А_n}, то говорят, что формула В выводима из совокупности формул Н и записывают

Н ├ В или А₁,А₂,…,А_n├ В.

 

Формулы множества Н, т.е. формулы А₁, А₂, …, А_n, называются посылками вывода или гипотезами. Переход в выводе от В_{i – 1} к В_i называется i-м шагом вывода.

 

Из о.1.1 следует, что:

1) всякая формула из множества Н является выводимой из множества Н;

2) всякая доказуемая формула выводима из множества Н;

3) если формулы С и С → В выводимы из множества Н, то формула В так же выводима из множества Н.

Замечание

1. Если Н = Æ или Н содержит только доказуемые формулы, то класс формул, выводимых из множества Н, совпадает с классом доказуемых формул.

2. Если множество Н содержит хотя бы одну недоказуемую формулу, то класс формул, выводимых из множества Н, шире класса доказуемых формул.

 

Свойства вывода из совокупности формул

1. Всякий начальный отрезок вывода из Н есть вывод из Н.

2. Если между двумя соседними формулами вывода из Н (или в начале, или в конце его) вставить некоторый вывод из Н, то полученная новая последовательность формул будет выводом из Н.

3. Всякая формула вывода из Н является выводимой из Н.

4. Если Н Ì W, то всякий вывод из Н является выводом из W.

5. Для того чтобы формула В была выводима из Н, необходимо и достаточно, чтобы существовал вывод В из Н.

Правила выводимости

Пусть Н и W – две совокупности формул исчисления высказываний. Обозначим их объединение через Н,W, т.е.

Н,W = Н È W.

В частности, если совокупность W состоит из одной формулы С, то

Н,С = Н È {С}.

1. Правило расширения: Н├ А

Н,W├ А

 

2. Правило удаления выводимой гипотезы: Н, С├ А, Н├ С

Н├ А

 

3. Н, С├ А, W├ С

Н, W├ А

 

4. Правило удаления импликации (обратно теореме дедукции): Н├ С → А

Н, С├ А

5. Правило введения конъюнкции: Н├ А, Н├ В

Н ├ А Ù В

 

6. Правило введения дизъюнкции: Н, А├ С, Н, В├ С

Н, АÚ В├ С

 

Рассмотрим пример на выводимость формулы из совокупности формул.

 

Пример 1. Доказать выводимость А → В ├ (С → А) → (С → В)

Доказательство

1. А → В	гипотеза
2. (А → В) → (С → (А → В))	аксиома 1 (х = А → В, у = С)
3. С → (А → В)	из 1,2 по МР
4. (С → (А → В)) → ((С → А) → (С → В))	аксиома 2 (х = С, у = А, z = В)
5. (С → А) → (С → В)	из 3,4 по МР

 

 

Вопрос 2. Теорема дедукции. Доказательство некоторых законов логики

 

В некоторых случаях работу по выводу формул облегчает так называемая теорема дедукции.

 

Т.2.1. (теорема дедукции, правило введения импликации)

Пусть Н –совокупность формул, А и В – формулы, причем Н, А├ В, тогда Н├ А → В, т.е.

Н, А├ В

Н├ А → В

В частности, если А├ В, то ├ А → В.

 

Важным следствием из теоремы дедукции является

 

Т.2.2. (обобщенная теорема дедукции)

Если из множества формул Н = {С₁,С₂,…,С_k} выводима формула А, то будет выводимой формула

С₁ → (С₂ → (С₃ →… (С_k → А)…)), т.е.

С₁,С₂,…,С_k ├ А

______________________________

├ С₁ → (С₂ → (С₃ →… (С_k → А)…))

 

Правила вывода, выводимости, и особенно теорема дедукции, позволяют доказать ряд законов логики:

 

1. Закон перестановки посылок: ├ (х → (у → z)) → (у → (х →z)) (1)

Доказательство

Рассмотрим множество формул Н = { х → (у → z), у, х}. Покажем, что

х → (у → z), у, х ├ z.

1. х → (у → z)	гипотеза
2. у	гипотеза
3. х	гипотеза
4. у → z	из 1,3 по МР
5. z	из 2,4 по МР

По обобщенной теореме дедукции доказуема формула (1).

 

Из закона перестановки посылок вытекает правило перестановки посылок в доказуемых формулах:

├ х → (у → z)

├ у → (х →z)

2. Закон соединения посылок: ├ (х → (у → z)) → (х Ù у →z) (2)

Доказательство

Рассмотрим множество формул Н = { х → (у → z), х Ù у}. Покажем, что

х → (у → z), х Ù у ├ z.

1. х → (у → z)	гипотеза
2. х Ù у	гипотеза
3. х Ù у → х	аксиома 3
4. х	из 2,3 по МР
5. у → z	из 1,4 по МР
6. х Ù у → у	аксиома 4
7. у	из 2,6 по МР
8. z	из 5,7 по МР

По обобщенной теореме дедукции доказуема формула (2).

Из закона соединения посылок вытекает правило соединения посылок в доказуемых формулах:

├ х → (у → z)

├ х Ù у →z

 

3. Закон разъединения посылок: ├ (х Ù у →z) → (х → (у → z))

Доказать самостоятельно.

 

Из закона разъединения посылок вытекает правило разъединения посылок в доказуемых формулах:

├ х Ù у →z

├ х → (у → z)

 

Вопрос 3. Связь алгебры высказываний с исчислением высказываний

В основе формализованного исчисления высказываний лежат понятия, относящиеся к так называемой области синтаксиса, т.е. понятия, представляющие собой некие абстрактные, лишенные смысла знаки и формальные действия с ними: алфавит, формула, аксиома, правило вывода, доказательство, теорема. Эти понятия принято называть синтаксическими.

В то же время алгебра высказываний пронизана содержательным смыслом: за каждой переменной стоит конкретное высказывание нашего языка, каждая формула может превращаться в конкретное составное высказывание, некоторые формулы могут превращаться только в истинные высказывания (тавтологии) и т.д. В данной сфере, являющейся областью семантики, каждое понятие наполнено каким-то внутренним содержанием, смыслом. Понятия истины и лжи, тождественной истинности и тождественной ложности формул, равносильности и логического следования формул считаются понятиями семантическими.

Каково же взаимоотношение между формализованным исчислением высказываний и алгеброй высказываний, между синтаксисом и семантикой?

 

Формулы ИВ можно интерпретировать как формулы алгебры высказываний. Для этого будем трактовать переменные ИВ как переменные алгебры высказываний, т.е. переменные в содержательном смысле, принимающие два значения: 1 и 0.

 

Операции Ù, Ú, →, ¯ определим так же, как в алгебре высказываний. При этом всякая формула ИВ при любых входящих в нее переменных будет принимать одно из значений 1 или 0, вычисляемое по правилам алгебры высказываний.

 

Сформулируем три основные теоремы, которые устанавливают связь между основными фактами алгебры высказываний и исчисления высказываний.

 

Т.3.1. Каждая формула, доказуемая в исчислении высказываний, является тождественно истинной (тавтологией) в алгебре высказываний.

Т.3.2. Каждая тождественно истинная формула (тавтология) алгебры высказываний доказуема в исчислении высказываний.

 

Теоремы 3.1 и 3.2 можно объединить в одну, которая по-сути дела является формулировкой свойства полноты исчисления высказываний.

 

Т.3.3. Формула тогда и только тогда доказуема в исчислении высказываний (является теоремой исчисления), когда она является тавтологией алгебры высказываний.

 

 

Т.3.4. (о выводимости)

Пусть А – некоторая формула ИВ; х₁,х₂,…,х_n – набор переменных, содержащий все переменные, входящие в формулу А; (α₁,α ₂,…,α _n) – произвольный фиксированный набор значений этих переменных; 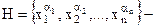конечная совокупность формул, где

1) Если на наборе (α₁,α ₂,…,α _n) значение формулы А равно 1, то Н ├ А.

2) Если на наборе (α₁,α ₂,…,α _n) значение формулы А равно 0, то Н ├ Ā.

 

 

Пример 2. Дана формула и набор значений переменных (1,0,0). Записать вывод формулы А или Ā из соответствующей совокупности формул.

Решение

(1,0,0) Þ х = 1, у = 0, z = 0 Þ соответствующее множество формул имеет вид

 

Найдем значение формулы А на указанном наборе:

Следовательно, Н ├ Ā, т.е. ├

 

Построим соответствующий вывод: