Выполнили
Студенты группы АТПз – 16
Загороднев Сергей
Багиянц Марат
Цель лабораторной работы
Ознакомление с алгоритмическими и программными средствами, позволяющими проводить численный гармонический анализ.
Ниже приведён листинг программы для получение смешанного спектрального сигнала со следующими параметрами: амплитуда первого сигнала – 4.25, частота 63 Гц, амплитуда второго сигнала – 3.3, частота 250 Гц.
>> % Определение спектральных характеристик сигнала с помощью
>> % быстрого преобразования Фурье
>>
>> % Частота квантования
>> fs = 2000;
>> nf = 1024;
>> % Временной интервал
>> t = 0:1/fs:1;
>> % Сигнал
>> y = 4.25*sin(2*pi*63*t) + 3.3*sin(2*pi*250*t);
>> % Случайная составляющая
>> y = y + 7*randn(size(t));
>> plot(t,y), pause
>> Y = fft(y,nf);
>> Pyy = Y.*conj(Y)/length(Y);
>> Y = []; y = [];
>> f = (fs/2)*(0:nf/2-1)/(nf/2);
>> plot(f, Pyy(1:length(f)))
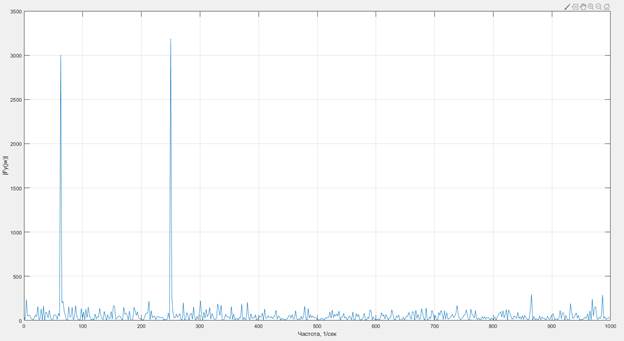
Получаем исходный сигнал для исследования (рис. 1) и его спектральную характеристику (рис. 2).
|
|
>> % Удалим из спектра сигналов одну из основных частот
>> % с параметрами амплитуды 3.3 и частотой 250 Гц
>> y = 4.25*sin(2*pi*63*t);
>> % И посмотрим на результат
>> y = y + 7*randn(size(t));
>> plot(t,y), pause
>> Y = fft(y,nf);
>>Pyy = Y.*conj(Y)/length(Y);
>>Y = []; y = [];
>>f = (fs/2)*(0:nf/2-1)/(nf/2);
>>plot(f, Pyy(1:length(f)))
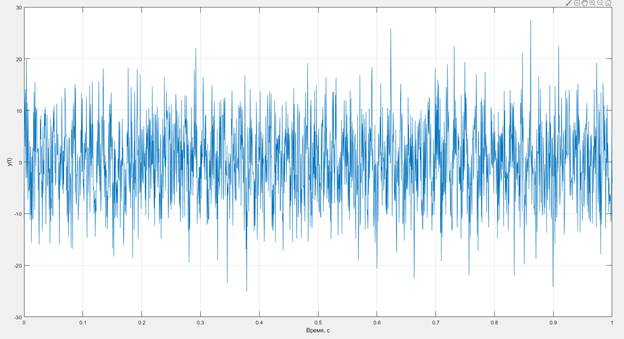
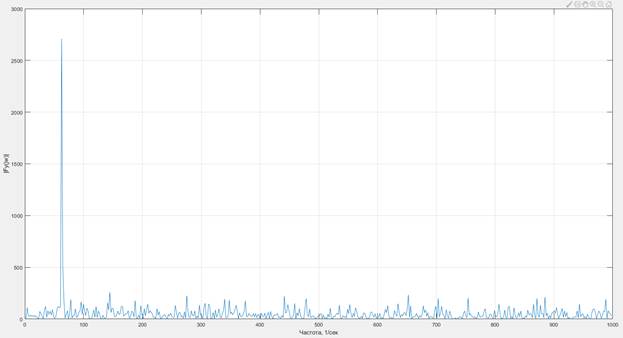
И посмотрим на результатирующие графики получившегося исходного сигнала (рис. 3) и спектра плотности мощности (рис. 4):
|
|
>> % Удалим из спектра сигналов вторую из основных частот
>> % с параметрами амплитуды 4.25 и частотой 63 Гц
|
|
>> y = 3.3*sin(2*pi*250*t);
>> % И посмотрим на результат
>> y = y + 7*randn(size(t));
>> plot(t,y), pause
>> Y = fft(y,nf);
>>Pyy = Y.*conj(Y)/length(Y);
>>Y = []; y = [];
>>f = (fs/2)*(0:nf/2-1)/(nf/2);
>>plot(f, Pyy(1:length(f)))
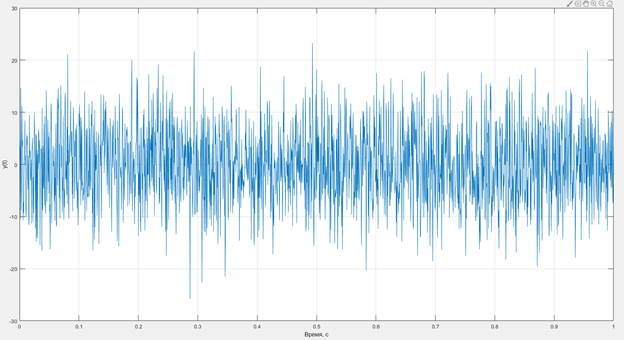
Результаты представлены на рис.5 – исходный график и рис.6 – спектр плотности мощности.
|
|
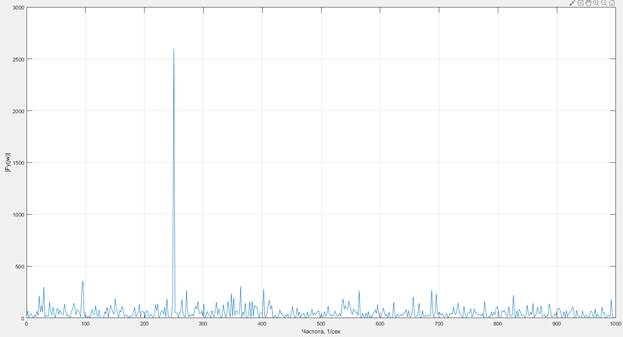
Вывод: рассматривая графики исходных процессов и их спектры мощности можно сделать однозначный вывод о невозможности выделения основных частот из зашумлённого сигнала без использования специальных инструментов преобразования Фурье.
1. Что такое гармонический анализ?
Гармонический анализ – представление сложного негармонического сигнала в виде суммы гармонических составляющих, входящих в спектр колебания.
2. Чем характеризуются гармонические составляющие?
Гармонические составляющие характеризуются частотой, амплитудой и начальной фазой.
3. Записать ряд Фурье в комплексном и косинусном виде.
Ряд Фурье в комплексном виде:
;
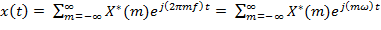Комплексные амплитуды:
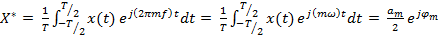
, где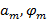 
– амплитуда и начальная фаза гармонического сигнала с частотой mf.
Ряд Фурье в косинусном виде:
;
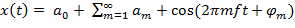4. Что такое комплексная амплитуда?
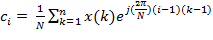– комплексные коэффициенты разложения функции в ряд Фурье называют комплексными амплитудами.
5. Как комплексная амплитуда описывает амплитуду и фазу гармонической составляющей?
Комплексная амплитуда – это комплексное число, модуль которого равен амплитуде, а аргумент – начальной фазе гармонического колебания. Пусть комплексная амплитуда 11-й гармоники равно 10+j10, аргумент равен arctg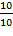 
= 45°, следовательно начальная фаза 11-й гармоники равна 45°.
|
|
6. На какую частоту отличаются соседние гармоники ряда Фурье?
На величину основной частоты.
7. Что такое амплитудный спектр?
Зависимость амплитуды гармонического сигнала в зависимости от его частоты.
8. Что такое фазовый спектр?
Зависимость начальной фазы гармонического сигнала от его частоты.
9. Что такое действительный спектр?
Действительный спектр – это зависимость величины действительной части комплексного числа, являющегося алгебраическим представлением амплитудно-фазовой характеристики гармоники сигнала в ЭВМ, разложенного в ряд Фурье, от частоты гармоники.
10. Что такое мнимый спектр?
Мнимый спектр – это зависимость величины мнимой части комплексного числа, являющегося алгебраическим представлением амплитудно-фазовой характеристики гармоники сигнала в ЭВМ, разложенного в ряд Фурье, от частоты гармоники.
11. Что такое спектр плотности мощности?
Спектр плотности мощности – это зависимость значений квадрата модуля комплексного числа, являющегося алгебраическим представлением амплитудно-фазовой характеристики гармоники сигнала в ЭВМ, разложенного в ряд Фурье, от частоты гармоники.
Спектр плотности мощности отражает распределение величин амплитуд гармоник, входящих в сигнал, разложенный в ряд Фурье, в зависимости от их частоты.
Плотность мощности для гармоники вычисляется как произведение комплексного числа на его комплексно-сопряженное (квадрат модуля), являющегося алгебраическим представлением амплитудно-фазовой характеристики члена ряда Фурье, который соответствует n-й гармонике, в который разложен исходный сигнал.
|
|
12. Покажите в используемой программе место разложения исходного сигнала в сумму гармонических составляющих. Поясните смысл параметров и результата выполнения соответствующей функции.
>> Y = fft(y,nf);
Y – вектор комплексных чисел размерностью nf,
y – исходный сигнал, состоящий из суммы некоторых гармонических составляющих и шума.
nf – размерность вектора
13. Напишите строчку, которая позволяет построить амплитудный, фазовый, действительный и мнимый спектры.
Амплитудный спектр:
A = abs(fft(y,nf));
Фазовый спектр:
P = angle(fft(y,nf));
Действительный спектр:
R = real(fft(y,nf));
Мнимый спектр:
I = image(fft(y,nf));