Задание 1. Составьте математические модели для следующих задач.
Вариант 1
Фирма выпускает три вида изделий. В процессе производства используются три технологические операции. На рис.1.1 показана технологическая схема производства изделий

Рис.1.1. Технологическая схема производства
Фонд рабочего времени ограничен следующими предельными значениями: для первой операции – 430 мин; для второй операции – 460 мин; для третьей операции – 420 мин. Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3, 2 и 5 рублей соответственно.
Постройте математическую модель, позволяющую найти наиболее выгодный суточный объем производства каждого вида продукции?
Вариант 2
При изготовлении изделий  и
и 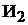 используются сталь и цветные металлы, а также токарные и фрезерные станки. По технологическим нормам на производство единицы изделия
используются сталь и цветные металлы, а также токарные и фрезерные станки. По технологическим нормам на производство единицы изделия  требуется 300 и 200 станко-часов соответственно токарного и фрезерного оборудования, а также 10 и 20 кг соответственно стали и цветных металлов. Для производства единицы изделия
требуется 300 и 200 станко-часов соответственно токарного и фрезерного оборудования, а также 10 и 20 кг соответственно стали и цветных металлов. Для производства единицы изделия 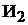 требуется 400, 100, 70 и 50 соответствующих единиц тех же ресурсов.
требуется 400, 100, 70 и 50 соответствующих единиц тех же ресурсов.
Цех располагает 12400 и 6800 станко-часами соответственно токарного и фрезерного оборудования и 640 и 840 кг соответственно стали и цветных металлов. Прибыль от реализации единицы изделия  составляет 6 руб. и от единицы изделия
составляет 6 руб. и от единицы изделия 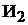 – 16 руб.
– 16 руб.
Постройте математическую модель задачи, используя в качестве показателя эффективности прибыль и учитывая, что время работы фрезерных станков должно быть использовано полностью.
Вариант 3
Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 условных единиц (усл. ед.), жиров – не менее 70 и витаминов – не менее 10 усл. ед. Содержание их в каждой единице продуктов  и
и  равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл. ед. Стоимость 1 ед. продукта
равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл. ед. Стоимость 1 ед. продукта  – 2 руб.,
– 2 руб.,  –3 руб.
–3 руб.
Постройте математическую модель задачи, позволяющую так организовать питание, чтобы его стоимость была минимальной, а организм получил необходимое количество питательных веществ.
Вариант 4
В районе лесного массива имеются лесопильный завод и фанерная фабрика. Чтобы получить 2,5  коммерчески реализуемых комплектов пиломатериалов, необходимо израсходовать 2,5
коммерчески реализуемых комплектов пиломатериалов, необходимо израсходовать 2,5  еловых и 7,5
еловых и 7,5  пихтовых лесоматериалов. Для приготовления листов фанеры по 100
пихтовых лесоматериалов. Для приготовления листов фанеры по 100  требуется 5
требуется 5  еловых и 10
еловых и 10  пихтовых лесоматериалов. Лесной массив содержит 80
пихтовых лесоматериалов. Лесной массив содержит 80  еловых и 180
еловых и 180  пихтовых лесоматериалов.
пихтовых лесоматериалов.
Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10  пиломатериалов и 1200
пиломатериалов и 1200  фанеры. Доход с 1
фанеры. Доход с 1  пиломатериалов составляет 160 руб., а со 100
пиломатериалов составляет 160 руб., а со 100  фанеры – 600 руб.
фанеры – 600 руб.
Постройте математическую модель для нахождения плана производства, максимизирующего доход.
Примечание. При построении модели следует учесть тот факт, что пиломатериалы могут быть реализованы только в виде неделимого комплекта размером 2,5  , а фанера – в виде неделимых листов по 100
, а фанера – в виде неделимых листов по 100  .
.
Вариант 5
С вокзала можно отправлять ежедневно курьерские и скорые поезда. Вместимость вагонов и наличный парк вагонов на станции указаны в табл.1.4.
Таблица 1.4
Исходные данные задачи №1.5
| Характеристики парка вагонов | Тип вагона | ||||
| Багажный | Почтовый | Плацкартный | Купейный | Мягкий | |
| Число вагонов в поезде, шт.: | |||||
| курьерском | – | ||||
| скором | |||||
| Вместимость вагонов, чел. | – | – | |||
| Наличный парк вагонов, шт. |
Постройте математическую модель задачи, на основании которой можно найти такое соотношение между числом курьерских и скорых поездов, чтобы число ежедневно отправляемых пассажиров достигло максимума.
Вариант 6
Управление городским автобусным парком решило провести исследование возможности более рациональной организации своей работы с целью снижения интенсивности внутригородского движения. Сбор и обработка необходимой информации позволили сделать вывод, что необходимое минимальное количество автобусов существенно меняется в течение суток (рис.1.2). Длительность непрерывного использования автобусов на линии равна 8 ч в сутки (с учетом необходимых затрат времени на текущий ремонт и обслуживание). График перекрывающихся смен представлен на рис.1.3.

Рис.1.2. Минимально необходимое количество автобусов на линии

Рис.1.3. График перекрывающихся смен
Постройте математическую модель, позволяющую узнать, какое количество автобусов необходимо выпускать на линию в каждой из смен при условии, что общее количество автобусов, выходящих на линию в течение суток, должно быть минимальным.
Вариант 7
Служба снабжения завода получила от поставщиков 500 стальных прутков длиной 5 м. Их необходимо разрезать на детали А и B длиной соответственно 2 и 1,5 м, из которых затем составляются комплекты. В каждый комплект входят 3 детали А и 2 детали B. Характеристики возможных вариантов раскроя прутков представлены в табл.1.5.
Таблица 1.5
Характеристики возможных вариантов раскроя прутков
| Вариант раскроя | Количество деталей, шт./пруток | Отходы, м/пруток | |
| А | B | ||
| 1 | |||
| 2 | |||
| 3 | 0,5 | ||
| Комплектность, шт./компл. |
Постройте математическую модель задачи, позволяющую найти план раскроя прутков, максимизирующий количество комплектов.
Примечание. В ЦФ могут входить не все переменные задачи.
Вариант 8
Малое предприятие выпускает детали А и В. Для этого оно использует литье, подвергаемое токарной обработке, сверлению и шлифованию. Производительность станочного парка предприятия по обработке деталей А и В приведена в табл.1.6.
Предполагая, что спрос на любую комбинацию деталей А и В обеспечен, постройте математическую модель для нахождения плана их выпуска, максимизирующего прибыль.
Таблица 1.6