В сетевых стохастических моделях на критическом пути находятся работы с вероятностной оценкой затрат времени на их проведение, что приводит к установлению общего времени выполнения комплекса работ с определенной степенью вероятности. С другой стороны, для выполнения этого комплекса работ назначается, как правило, директивный срок, который является детерминированной величиной. В связи с этим возникает вопрос, какова вероятность выполнения данного комплекса работ в заданный срок, или, насколько достоверна оценка затрат времени по критическому пути.
Оценка достоверности затрат времени по критическому пути проводится на основе следующих положений теории вероятностей, применяемых при статистической обработке случайных величин.
1. Если критический путь состоит из многих (п >10) работ, сроки завершения которых распределены случайно, то распределение возможных сроков исполнения суммы работ в окрестностях tкр близко к нормальному.
2. Нормальное распределение случайной величины характеризуется средним значением и дисперсией.
В данном случае средней величиной служит продолжительность критического пути tкр.
Дисперсия критического пути Dкр определяется суммой дисперсий работ Dij,кр, лежащих на критическом пути, так как вероятностные оценки продолжительности этих работ являются независимыми случайными величинами и дисперсии работ можно складывать при оценке дисперсии пути
Dкр = ∑Dij,кр.
3. Вероятность выполнения директивного срока tд определяется функцией нормального распределения (функцией Лапласа) или интегралом вероятности.

 tд - tкр
tд - tкр
 Р = Ф = Ф (z)
Р = Ф = Ф (z)
σкр
Аргумент z функции Р представляет величину относительного отклонения продолжительности критического пути tкр и директивного срока tд.
Величина среднего квадратичного отклонения σкр продолжительности критического пути равна σкр = √ Dкр.

 Р
Р
1,0 I II





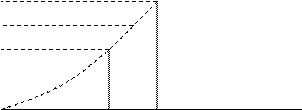 |
 0,655
0,655
0,5
 0,35 t'кр = tкр,наим
0,35 t'кр = tкр,наим
t''кр = tкр,наиб
t
t’кр tкр t’’кр
Кривая нормального распределения (I) – симметричная кривая с наибольшей плотностью (вероятностью) при среднем значении величины tкр.
Кривая функции Лапласа (II) характеризует вероятность нахождения величины tкр в заданном интервале. С увеличением t растете величина Р, приближаясь к единице.
* Значения функций Р при заданных значениях аргумента z определяются по таблицам функции Лапласа.
При оценке достоверности затрата времени по критическому пути на кривой функции Р можно выделить следующие характерные точки:
tд = tкр; z = 0; Р = 0,5
tд > tкр; z = 0,4; Р = 0,655 - в этом случае достоверность выполнения работ в срок принято считать высокой;
tд < tкр; z = -0,4; Р = 0,35 - при снижении вероятности появляется опасность срыва сроков комплекса работ.
В практике сетевого планирования установлено, что если значения аргумента z находятся в интервале {-0,4≤ z ≤ 0,4}, то ход работ считается нормальным и выполнение комплекса работ в срок достоверно.
По граничным значениям аргумента z (z = ±0,4) можно вычислить величины наибольшей и наименьшей продолжительности критического пути, которые также характеризуют интервал { tкр,наим ≤ tкр ≤ tкр, наиб } значений tкр при достоверном выполнении работ в срок:
tкр, наиб = tд + 0,4* σ = tд + 0,4*√ Dкр;
tкр, наим = tд - 0,4* σ = tд - 0,4*√ Dкр.