Студент должен:
знать:
- сущность средних величин, единицы их измерения;
- виды средних величин;
- методы расчёта средних показателей;
уметь:
- рассчитывать средний уровень изучаемого явления.
Средние величины абстрактны, представляют собой обобщающие
показатели, рассчитываются на основе массовых данных, измеряются в той же размерности, что и признак.
Приняты следующие обозначения:
х1, х2, х3, ….. хn (хi) – варианты, или индивидуальные значения признака;
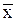- средняя величина признака;
f – частота признака;
Σ – знак суммирования;
n – количество единичных признаков;
i – порядковый номер;
- серединное значение признака;
Wi – произведение вариантов на частоту
ω - частости - % к итогу.
Виды средних величин:
1. Простая средняя арифметическая (невзвешенная) – это количество суммарного признака, делённое на число показаний:
= 
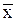Применяется для единичных значений признаков.
2. Взвешенная средняя арифметическая имеет в числителе сумму произведений варианта на частоту, а в знаменателе – сумму частот:
= 
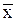Применяется, когда значение признака повторяется несколько раз.
В интервальном ряду распределения определяется серединное значение , затем производится взвешивание: f.
В закрытом интервале серединное значение определяется как полусумма значений нижней и верхней границ. В открытом интервале предполагается, что расстояние между границами интервала такое же, как в соседнем интервале.
Тогда окончательная формула: 
= 
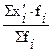
3. Простая средняя гармоническая – это величина, обратная средней арифметической.
|
|
= 
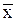Применяется, когда произведения по каждому признаку равны.
4. Взвешенная средняя гармоническая:
= 
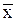Применяется, когда даны произведения вариантов на частоту, а частота
отсутствует.
Средняя геометрическая
Применяется для отношения двух чисел, а также в рядах распределения
в виде геометрической прогрессии.
Структурные средние величины
- мода (Мо) – это наиболее часто встречающаяся варианта,
- медиана (Ме) – это величина, которая делит численность упорядоченного вариационного ряда на 2 равные части.
Вопросы самоконтроля
1. При каких условиях применяются средние арифметические
взвешенная и невзвешенная величины?
2. При каких условиях применяются средние взвешенные арифметическая и гармоническая величины?
3. В чём различие моды и медианы?
Тема 2.4 Показатели вариации
Студент должен:
знать:
- сущность и виды показателей вариации;
- их значение;
уметь:
- оценить степень вариации изучаемого признака путём расчёта абсолютных, средних и относительных показателей вариации.
- оценить степень вариации изучаемого признака путём расчёта
абсолютных, средних и относительных показателей вариации.
Вариации признаков – это различие индивидуальных значений признака внутри изучаемой совокупности.
Показатели вариации следующие:
Абсолютные показатели
- размах вариации – это разность между наибольшими и наименьшими значениями вариант:
R = Xmax - Xmin
- линейное отклонение – это разность индивидуальных значений и средней величины:
|
|
d = 
Средние показатели
- среднее линейное отклонение – это средняя арифметическая из отклонений индивидуальных значений от средней:
d =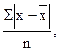 
или d =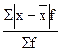 
- средний квадрат отклонений (показатель дисперсии) – это средняя из отклонений, возведенных в квадрат:
δ2 =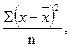 
или δ2 = 
- среднее квадратическое отклонение – это кореньквадратный из дисперсии – среднего квадрата отклонений:
δ = 