Расчет одиночных болтов.

1. Болт затянут, внешней нагрузки нет. Болт «черный», (установлен с зазором )

 

F

D1

d

F

–усилие (

 

Рис 1. Болтовое соединение.

 

Известны; Q: d, d₁ (d₁ ≈d-p. p- шаг резьбы).

Условие прочности: σ= , отсюда d₁ = ;

по d₁ определяется d- стандартный диаметр болта, где

d₁ - внутренний диаметр резьбы

[σ] - допускаемое напряжение

[σ] = =

Пределы напряжение: σ_{в -} предел прочность, σ_т - предел текучести, S- запас прочности.

11. Болт затянут. Нагрузка перпендикулярная оси болта (в плотности стыка).

2.1 Болт «чёрный» (есть зазор∆)

Условия прочности соединения - сила трения должна быть больше двигающей силы F.

F_тр= Q ƒ ≥ F

Q - нормальная сила, перпендикулярна плоскость стыка – сила затяжки,

ƒ- коэффициент трения.

(Сталь по стали без смазки ƒ= 0,15÷0,20)

Условия затяга определяем Q. Q =

Условия прочности болта: Ϭ , отсюда

d₁ = определяем d (ГОСТ) (ближайшей больший).

111. Болт «чистый» (∆=0)

В этом случае затяжку болта Q не учитывают (силы трения в запас прочности).

Болт работает на срез в плоскости стыка.

Условия прочности:

(округлить по ГОСТу).

 

1V. Болт затянут. Внешняя нагрузка F_в дополнительно растягивает болт.

F_max

F F_в

Q

(1- )*F_в

Q ∆

∆

∆δ ∆_ст

Рис 2. Диаграмма предварительно затянутого болтового соединения нагруженное внешней силой F_в

Здесь: Q – усилие затяга,Q ҆ - остаточная нагрузка стыке,F_в – внешняя нагрузка

∆δ – деформация болта (растяжение), ∆ст – деформация стыка (сжатие)

∆ - Совместная деформация после приложения внешней нагрузи.

Максимальная нагрузка F_max = F_в + Q ҆ или F_max =Q + χF_в, где

χ- коэффициент внешней нагрузки.

Известен: Закон Гука ∆= , или ∆=Fλ,

где λ- податливость λ .

Здесь: F- осевая сила; Ɩ – начальная длина; E- модуль упругости; A-площадь поперечного сечения

Определим коэффициент внешней нагрузки из условия совместимости.

Общая деформация: ∆= χ F_в λ_б = (1-χ)F_вλ_ст λ=

Приведение нагрузок (сил и моментов) к заданному центру.

Из теоретической механики известно, что любую систему сил и моментов можно свести к двум параметрам, главному вектору и главному моменту .

F₁ F₂ F_i M=Fв

F

.0 F в 0

М₁ Рис 4. Вектор - момент

 

 

0 - точка приведения.

Рис 3. Приведение сил к центру.

Главный вектор и главный момент (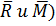 можно разложить по осям координат (R_x; R_y; R_z; M_x; M_y; M_z)

y

x

z

Рис 5. Разложение главного вектора и главного момента по осям координат.

R_x= ΣF_ix M_x=ΣM_ix

R_y= ΣF_iy M_y=ΣM_iy

R_z=ΣF_izM_z=ΣM_iz

R_x,y,z – сумма проекций всех сил на соответствующую ось x,y,z

M_x,y,z - сумма проекций всех моментов на соответствующую ось x,y,z

Предварительно внешние силы и моменты необходимо разложить по осям параллельным x,y,z

Пример одноступенчатого редуктора.

Задача - найти наиболее нагруженный болт.

Редуктор нагружен внешними силами F₁ u F₂, предварительно разложенными по осям координат, параллельным центральным.

у х F_y1

F_x1

y₁ z₁ F_z1

x₁

F_y2 0 z

F_x2 z₂ x₂

У₂

Рис 6. Схема нагрузок редуктора и их координат.

1. Центр приведения – центр симметрии болтов (точке О), где

x₁, y₁, z_{1 –}координаты силы F₁; x₂, y₂, z₂ – координаты силы F₂

Центр приведения – центр плоской фигуры, образованной сечением болтов (в общем случае, сечением элементов крепления).

Силы, приложенные в этом центре (R_x,R_y, R_z) дают малое перемещение объекта в направлении каждой силы поступательно, (весь объект перемещается параллельно самому себе) нагружая элементы крепления одинаково.

Моменты (М_x, M_y, M_z) относительно соответствующих центральных осей x y z, поворачивают корпус редуктора относительно этих осей, нагружая элементы крепления с одой стороны от осей дополнительной нагрузкой, пропорциональной расстоянию болтов от каждой оси; с другой стороны от каждой оси нагрузка в болтах уменьшается и в расчетах не учитывается.

2_.Приведение сил и моментов к центру 0.

R_x= ΣF_ix = F_x1+F_x2

R_y = ΣF_iy = F_y1+F_y2

R_z= ΣF_iz = F_z1

M_x = ΣM_ix = - F_y1z₁ +F_z1y₁+ F_y2z₂

M_y = ΣM_iy = + F_x1z₁ -F_z2x₁- F_x2z₂

M_z = ΣM_iz = - F_x1y₁ +F_y1x₁- F_x2y₂- F_y2x₂

 

_{у х}

М_у М_х

R_y R_x в

0 R_z M_z z

а

Рис 7.Нагрузки, приведенные к центру.

Три фактора (R_x,R_z, М_у) создают горизонтальные нагрузки. Их рассматривают отдельно от других факторов, создающих вертикальные реакции.

Три фактора (R_у,М_z, М_х) создают вертикальные силы в болтах.

Горизонтальные силы (в плоскости стыка).

x

F_My a

F_Rz F_Rz

F_Rx F_Rx F_My

R_x в

M_y

0 R_z

 

F_My

F_Rz F_Rz

F_Rx F_My F_Rx

Рис 8. Расчетная схема в горизонтальной плоскости.

Здесь - расстояния от центра приведения до осей болтов

1. Реакция болтов на силу R_x = Сила сдвигает основание редуктора поступательно в направлении силы R_x (в пределах упругости), поэтому реакции болтов одинаковы.

Условие равновесия: ΣF_ix=0=R_x-4F_Rx=0, откуда

2. Аналогичная реакция болтов на силу R_z:

Условие равновесия: ΣF_iz=0=R_z-4F_Rz=0

3. Реакция болтов на момент М_у. Силы реакции противоположны малым перемещениям (они одинаковы по величине, так как все они – на расстоянии от центра, но разные по направлению – перпендикулярны радиусу .

Наиболее нагруженный болт в горизонтальной плоскости тот где векторная сумма сил – максимальна.

Удобно сначала сложить векторы F_Rx u F_Rzзатем результирующий и вектор F_My.(рис 9.)

Определим угол α: ;

Найдем угол β: tgβ= ; β= acrctg

Угол между векторами u : .

Суммарную силу F_∑ определим.

 

α β по теореме косинусов.

F_∑ F_My

в

β a

Рис 9. К определению суммарной силы F_∑.

Суммарная сила F_Σравна сумме трех векторов.

Условия прочности соединения: F_тр ≥ F_Σ

F_тр = Q ƒ ≥ F_Σ,отсюдаQ= . Q- сила затяжки болта, которая используется в окончательном расчете, где определяется F_max:

F_max =Q + χ F_в

 

Определение осевых сил в болтах от нагрузок R_y(F_Ry); M_x(F_Mx); M_z(F_Mz).

 

 

y x

№1 №2

R_y

в

z

№4 a №3

Рис 10. Расчетная схема к определению осевых сил в болтах.

Определение сил от каждого из трех факторов (R_у,М_z, М_х).

1. Определим реакцию болтов на внешнюю силу R_у. Так как сила приложена к центру плоской фигуры, образованной сечением болтов, то все болты - в одинаковых условиях. Основание перемещается по направлению силы R_у, (в пределах упругости болтов), а в болтах возникают одинаковые реакция на силу R_у.

Условие равновесия::ΣF_iу=0=R_у-4F_Rу=0

2. Определим реакцию болтов на внешний момент М_х. Момент поворачивает (в пределах упругости), основание относительно оси х так, что болты №1 и №4 дополнительно растягиваются, а болты №2 и № 3 ослабляются и в расчете не учитываются.

 

у х

∆₁ М_х №2,№3

№1,№4 ∆₂

Рис 11. К определению реакции болтов и момент М_х.

Условие равновесия: ΣM_ix=0= M_x – 2F_Mxa=0 =>F_Mx=

3. Определим реакцию болтов на внешний момент М_z. Момент М_z поворачивает (в пределах упругости) основание относительно оси z так, что болты №1 и №2 дополнительно растягиваются, а болты №3 и №4 ослабляются и в расчете не учитываются.

Условие равновесия: ΣM_iz=0= M_z – 2F_Mв=0 =>F_Mz=

Очевидно, что наиболее нагружен болт №1, где F_Σ равна

F_Σ = F_Ry+F_My+F_Mz=F_в (на середину)

Где F_в – внешняя нагрузка на болт от всех факторов.

Расчет болта №1 как предварительно затянутого.

F

Q

F_max

 

 

Рис 12. К определению максимальной осевой нагрузки на болт

F_max =Q + χ F_в

где χ- коэффициент внешней нагрузки (χ 0,25)

Затем определим диаметр болта из условий прочности:

Ϭ , откуда определим d₁ и затем d (диаметр стандартного болта).

d₁ = Определяем d (ГОСТ) с учетом шага резьбы и округление в большую сторону.