Нахождение начального решения методом Северо-Западного угла

 

 

 

Нахождение начального решения методом минимальной стоимости

 

Значение целевой функции L(x⁰) при начальном решении по методу минимальной стоимости меньше, чем по методу северо-западного угла, поэтому примем его за начальное решение.

2. Проверка решения х⁰ на вырожденность

Количество ненулевых элементов в решении х⁰ равно 8, проверим условие N= m + n -1= 4 + 5 - 1=8, т.е. решение х⁰ не является вырожденным.

 

=

 

Таблица 2.1. Проверка плана х⁰ на оптимальность.

 

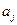
						Ui
		12
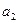
							-2
							-1
Vj

 

 

План х⁰ не является оптимальным, т.к. есть два положительных решения и .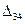

. Начиная с разрешающего элемента в клетке (34), строим замкнутый цикл, вершинами которого будут цифры плана, отличные от нуля. Помечаем вершины цикла знаками «+» и «−» поочередно, начиная с разрешающего элемента. Находим величину сдвига по циклу - минимальный из элементов цикла, помеченных знаком «−».

X₃₄ – разрешающий элемент 0*. Минимальная поставка для отрицательных вершин

θ₁=min 8,14 =8. Организуем следующий цикл:

 

+25 8 - 33 0

 

 

- 14? + 6 8

 

3. Проверка плана х' на оптимальность

Таблица 2.2

						Ui
		12
							-2
							-1
Vj

 

 

план не оптимальный.

– разрешающий элемент 0*. Минимальная поставка для отрицательных вершин

Θ₂=min 31,6 = 6.

 

Организуем второй цикл:

 

31 0 25 6

 

3 6 9 0

 

Строим новый план х²,

 

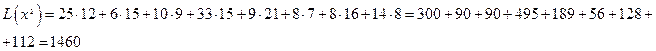
Таблица 2.3 – Проверка плана х² на оптимальность

 

						Ui
		12
							-1
Vj				-2

 

 

Все Оптимум достигнут

 

План 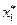оптимален, но – это признак альтернативного оптимума, х₄₁ – разрешающий элемент, находим альтернативные решения х³.

 

- +   + -

- +   + -

25 10 11 24

 

 

? 14 14 0

 

 

Ответ: , ,

 

Решить транспортную задачу в среде Excel

В ячейках А1-Е5 вводим тарифы:

 

 

В ячейках G1-5 задаем запасы, а в ячейках А6-Е6 – заказы:

 

 

Теперь задаем область поиска решения, размер которой должен совпадать с размерностью исходной задачи. В качестве начальных значений вводим единицы:

 

 

Отдельно задаем ячейку целевой функции, используя встроенную функцию СУММ ПРОИЗВ:

 

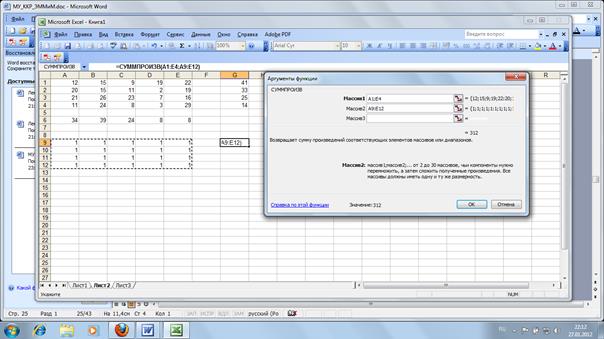
В ячейках F9-12 задаем суммы по строкам, а в ячейках А13-Е13 – по столбцам:

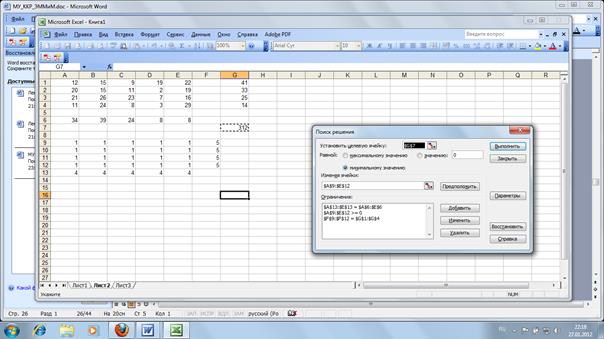
В окне Поиска решения в Параметрах выбираем метод сопряженных градиентов:

Задаем ограничения и изменяемые ячейки:

 

 

 

Получим решение: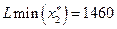

 

 

;
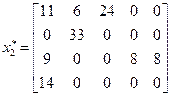