Методика статистической обработки результатов наблюдений
Излагаемая далее методика относится к прямым измерениям с многократными наблюдениями. Предполагается, что наблюдения равноточные: выполняются данным экспериментатором в одинаковых условиях, одним и тем же прибором. Методика сводится к следующему:
1. Проводят N наблюдений (единичных измерений) и фиксируют N результатов наблюдений одного и того же значения физической величины (N показаний прибора):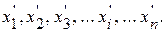 
2. Исключают известные систематические погрешности из результатов наблюдений и получают исправленные результаты x 1, x 2, …, x i, …, xn.
3. Находят среднее арифметическое значение исправленных результатов наблюдений по формуле 
и принимают 
за результат измерения.
4. Вычисляют оценку среднеквадратического отклонения результатов наблюдений:
а) находят отклонения от среднего арифметического 
… 
;
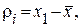
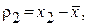б) проверяют правильность вычислений; если они правильны, то
;
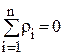в) вычисляют квадраты отклонений от среднего
...; 
...; 
;
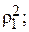
г) определяют оценку среднеквадратического отклонения
;
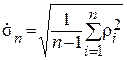д) находят значение относительной среднеквадратической случайной погрешности по формуле
5. Вычисляют оценку среднеквадратического отклонения результата измерения
6. Проверяют гипотезу о том, что распределение результатов наблюдений – гауссовское (нормальное).
7. Вычисляют доверительные границы случайной погрешности результата измерения:
а) задаются коэффициентом доверия α (доверительной вероятностью);
б) по специальным таблицам определяют значение коэффициента 
, соответствующее заданному коэффициенту доверия 
;
в) находят значение 
;
г) вычисляют доверительные границы 
;
д) определяют доверительный интервал 
.
8. Записывают результат измерения.
Суммирование погрешностей
Систематические погрешности Si, если они известны или достаточно точно определены, суммируют алгебраически (с учетом собственных знаков):
S ∑= 
.
Нередко систематические погрешности по своей природе носят характер случайных. Поэтому имеется тенденция при суммировании рассматривать все погрешности как случайные.
Случайные погрешности суммируют с учетом их взаимных корреляционных связей. Из теории вероятностей известно, что дисперсия двух случайных величин
где 
и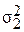 
– дисперсии случайных величин;
К – коэффициент корреляции между ними.
Отсюда суммарная среднеквадратическая погрешность
Обычно информация о мере корреляционных связей отсутствует, поэтому на практике рассматривают два крайних случая: К≈0 и К≈±1. При этом:
а) некоррелированные (вызванные взаимно независимыми источниками или причинами) погрешности суммируются геометрически:
,
где 
среднеквадратическая оценка погрешности, обусловленной
i -м источником;
б) случайные погрешности, сильно или жестко коррелированные (К≈±1), суммируются с учетом следующих предпосылок.
Если данная причина вызывает в различных узлах прибора изменения погрешностей в одном и том же направлении, то погрешности складывают, т.е.
Если же изменения получаются противоположными погрешности вычитают, т.е.
.
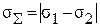