Вариант 2
Задание №1.
Бросаются два игральных кубика. Найти вероятность того, что сумма выпавших очков
1) равна k - 1;
2) не превосходит k;
3) больше m -2.
Задание №2.
В ящике находится n гвоздей, (n+2) шурупов и ( n+3 ) болтов.
1) Наудачу выбирают две детали. Найдите вероятность того, что достали:
а) два шурупа; б) гвоздь и болт
2) Наудачу выбирают три детали. Найдите вероятность того, что достали:
а) три болта; б) болт, гвоздь и шуруп.
Задание №3.
На предприятии работают две бригады рабочих: первая производит в среднем ¾ продукции с процентом брака 4%, вторая – ¼ продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие окажется бракованным.
Задание №4
Производятся четыре выстрела по мишени. Вероятность попасть в цель при одном выстреле равна 0, n. Найдите вероятность того, что
1) будет два попадания;
2) будет не менее трех попаданий;
Задание №5
При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:
а) будут иметь дефекты отделки 60 пар;
б) не будут иметь дефектов отделки от 120 до 148 пар?
Задание №6
Задан закон распределения дискретной случайной величины Х:
| Хi | -2 | -1 | |||||
| рi | 0,2 | 0, 31 | 0,24 | р | 0,07 | 0,04 | 0,01 |
Найти:
а) неизвестную вероятность р;
б) функцию распределения F(x) и построить её график;
в) математическое ожидание 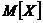 , дисперсию
, дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение  данной случайной величины;
данной случайной величины;
г) отразить математическое ожидание и СКО на многоугольнике распределения.
Задание №7
Математическое ожидание нормально распределенной случайной величины Х равно m, ее среднее квадратичное отклонение  . Выполните следующие задания:
. Выполните следующие задания:
1) напишите формулу функции плотности распределения вероятности и схематично постройте ее график;
2) найдите вероятность того, что СВ X примет значения из интервала  , где
, где  ,
, 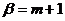
Задание №8
Рассчитать и построить гистограмму относительных частот по сгруппированным данным

| 
| 
|
| (2; 4] | ||
| (4; 6] | ||
| (6; 8] | ||
| (8; 10] | ||
| (10; 12] |
Задание №9
Известно эмпирическое распределение выборки некоторой СВ Х:

| k+n | ||||||

| 25- m | 8+ m |
1. Найдите точечную оценку математического ожидания СВ Х и точечную оценку среднего квадратического отклонения СВ Х
2. Постройте полигон частот и отразите на нем значение выборочного среднего и выборочного отклонения.
k – количество букв в полном имени студента;
m – количество букв в фамилии студента;
N – номер студента в списке группы.
Вариант 3
Задание №1.
Бросаются два игральных кубика. Найти вероятность того, что сумма выпавших очков
1) равна k - 1;
2) не превосходит k;
3) больше m -2.
Задание №2.
В ящике находится n гвоздей, (n+2) шурупов и ( n+3 ) болтов.
1) Наудачу выбирают две детали. Найдите вероятность того, что достали:
а) два шурупа; б) гвоздь и болт
2) Наудачу выбирают три детали. Найдите вероятность того, что достали:
а) три болта; б) болт, гвоздь и шуруп.
Задание №3.
В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель – 0,85. Проведена проверка качества одной пары обуви. Найти вероятность того, что эта пара обуви отремонтирована качественно.
Задание №4
Производятся четыре выстрела по мишени. Вероятность попасть в цель при одном выстреле равна 0, n. Найдите вероятность того, что
1) будет два попадания;
2) будет более трех попаданий;
Задание №5
Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что из 300 новорожденных окажется:
а) ровно 150 мальчиков;
б) от 150 до 200 девочек?
Задание №6
Задан закон распределения дискретной случайной величины Х:
| Хi | -2 | -1 | |||||
| рi | 0,04 | 0, 08 | 0,32 | 0,31 | 0,15 | 0,08 | р |
Найти:
а) неизвестную вероятность р;
б) функцию распределения F(x) и построить её график;
в) математическое ожидание 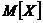 , дисперсию
, дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение  данной случайной величины;
данной случайной величины;
г) отразить математическое ожидание и СКО на многоугольнике распределения.
Задание №7
Математическое ожидание нормально распределенной случайной величины Х равно m, ее среднее квадратичное отклонение  . Выполните следующие задания:
. Выполните следующие задания:
1) напишите формулу функции плотности распределения вероятности и схематично постройте ее график;
2) найдите вероятность того, что СВ X примет значения из интервала  , где
, где  ,
, 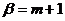
Задание №8
Рассчитать и построить гистограмму относительных частот по сгруппированным данным

| 
| 
|
| (-6; -2] | ||
| (-2; 2] | ||
| (2; 6] | ||
| (6; 10] | ||
| (10; 14] |
Задание №9
Известно эмпирическое распределение выборки некоторой СВ Х:

| k+n | ||||||

| 25- m | 8+ m |
1. Найдите точечную оценку математического ожидания СВ Х и точечную оценку среднего квадратического отклонения СВ Х
2. Постройте полигон частот и отразите на нем значение выборочного среднего и выборочного отклонения.
k – количество букв в полном имени студента;
m – количество букв в фамилии студента;