Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка в общем случае содержит:
1) независимую переменную x;
2) зависимую переменную (функцию) y;
3) первую производную функции: y’.
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или (и) «игрек», но это не существенно
– важно чтобы в ДУ была первая производная, и не было производных высших порядков.
Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют данному уравнению.
Такое множество функций часто имеет вид  (C – произвольная постоянная), который называется общим решением дифференциального уравнения.
(C – произвольная постоянная), который называется общим решением дифференциального уравнения.
Пример 1
Решить дифференциальное уравнение

1. Нужно переписать производную в другом виде. Вспоминаем громоздкое обозначение  , которое многим из вас наверняка казалось нелепым и ненужным. В диффурах рулит именно оно!
, которое многим из вас наверняка казалось нелепым и ненужным. В диффурах рулит именно оно!
Итак:

2. Смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.
Дифференциалы dy и dx – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:

Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
3. интегрирование дифференциального уравнения. Всё просто, навешиваем интегралы на обе части:

Разумеется, интегралы нужно взять. В данном случае они табличные:

Как мы помним, к любой первообразной приписывается константа. Здесь два интеграла, но константу достаточно записать один раз (т.к. константа + константа всё равно равна другой константе). В большинстве случаев её помещают в правую часть.
Строго говоря после того, как взяты интегралы, дифференциальное уравнение считается решённым.
Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде.
Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть,  – это общий интеграл.
– это общий интеграл.
Ответ в такой форме вполне приемлем, но нет ли варианта получше? Давайте попытаемся получить общее решение.
П ервый технический приём, он очень распространен и часто применяется в практических заданиях: если в правой части после интегрирования появляется логарифм, то константу во многих случаях (но далеко не всегда!) целесообразно записать тоже под логарифмом. И записать НЕПРЕМЕННО, если получились одни логарифмы (как в рассматриваемом примере).
То есть, ВМЕСТО записи

пишут
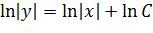
Зачем это нужно? А для того, чтобы легче было выразить «игрек». Используем свойство логарифмов

В данном случае:

Теперь логарифмы и модули можно убрать:
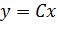
Функция представлена в явном виде. Это и есть общее решение.
Ответ: общее решение: 
Проверка ответов
В нашем случае это делается совсем просто, берём найденное решение и дифференцируем его:

После чего подставляем 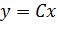 и производную
и производную 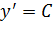 в исходное уравнение:
в исходное уравнение:


– получено верное равенство, значит, общее решение удовлетворяет уравнению, что и требовалось проверить.
Придавая константе различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Ясно, что любая из функций,  , и т.д. удовлетворяет дифференциальному уравнению.
, и т.д. удовлетворяет дифференциальному уравнению.
Иногда общее решение называют семейством функций. В данном примере общее решение – это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
Некоторые замечания о дифференциальных уравнениях:
1) В этом примере нам удалось разделить переменные. Всегда ли это можно сделать? Нет, не всегда. И даже чаще переменные разделить нельзя. Например, в однородных уравнениях первого порядка, необходимо сначала провести замену. В других типах уравнений, например, в линейном неоднородном уравнении первого порядка, нужно использовать различные приёмы и методы для нахождения общего решения. Уравнения с разделяющимися переменными, которые мы рассматриваем– простейший тип дифференциальных уравнений.
2) Всегда ли можно проинтегрировать дифференциальное уравнение? Нет, не всегда.
3) Всегда ли можно из общего интеграла найти общее решение, то есть, выразить «игрек» в явном виде? Нет не всегда.
Пример 2 Задача Коши (частное решение ДУ, удовлетворяющее заданному начальному условию).
Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию

Решение:
Сначала находим общее решение. В уравнении нет переменной «икс», но главное, в нём есть первая производная.
Переписываем производную в нужном виде:
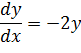
Разделяем переменные

Интегрируем уравнение:
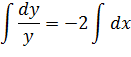

Общий интеграл получен.
Здесь константа с надстрочной звездочкой, дело в том, что она будет преобразована в другую константу.
Теперь пробуем общий интеграл преобразовать в общее решение (выразить «игрек» в явном виде).
Известно, что:

В данном случае:

Используя свойство степеней, перепишем функцию следующим образом:

Если С* константа, то  – тоже некоторая константа, переообозначим её буквой C:
– тоже некоторая константа, переообозначим её буквой C:

– при этом модуль убираем, после чего константа сможет принимать как положительные, так и отрицательные значения
«Снос» константы – это второй технический приём, который часто используют в ходе решения дифференциальных уравнений.
Итак, общее решение:

На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию

Необходимо подобрать такое значение константы, чтобы выполнялось начальное условие.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:



Теперь в общее решение подставляем найденное значение константы
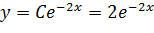
Ответ: частное решение уравнения

Выполним проверку. Проверка частного решение включает в себя два этапа:
Первый этап. Сначала необходимо проверить, а действительно ли найденное частное решение удовлетворяет начальному условию? Вместо «икса» подставляем ноль:

начальное условие выполняется.
Второй этап. Берём полученное частное решение и находим производную:
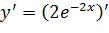

Подставляем  в исходное уравнение:
в исходное уравнение:


– получено верное равенство.
Вывод: частное решение найдено правильно.
Переходим к более содержательным примерам.
Пример 3
Решить дифференциальное уравнение

Решение: переписываем производную в нужном нам виде:

Оцениваем, можно ли разделить переменные?
Переносим второе слагаемое в правую часть:

И перекидываем множители по правилу пропорции:

Переменные разделены, интегрируем обе части:

Интеграл левой части:

Интеграл правой части:

Тогда, с учетом первой технической рекомендации (константу под знак логарифма):

Теперь пробуем упростить общий интеграл. С помощью известных свойств максимально «упаковываем» логарифмы.



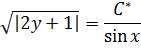
приводим общий интеграл к виду  :
:

В принципе, это можно записать в ответ, но здесь ещё уместно возвести обе части в квадрат и переобозначить константу:
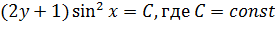
Примечание: общий интеграл часто можно записать не единственным способом. Таким образом, если ваш результат не совпал с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.



Третий технический совет: если для получения общего решения нужно выполнить значительное количество действий, то в большинстве случаев лучше воздержаться от этих действий и оставить ответ в виде общего интеграла. Это же касается и «плохих» действий, когда требуется выразить обратную функцию, возвести в степень, извлечь корень и т.п. Дело в том, что общее решение будет смотреться вычурно и громоздко – с большими корнями, знаками и прочим математическим трэшем.
Проверка:

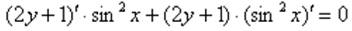


делим каждое слагаемое на 

делим каждое слагаемое на 


Получено в точности исходное дифференциальное уравнение, значит, общий интеграл найден правильно.
Пример 4
Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию 
Выполнить проверку.
Это пример для самостоятельного решения.
Напоминание
алгоритм состоит из двух этапов: 1) нахождение общего решения; 2) нахождение требуемого частного решения.
Проверка тоже проводится в два шага
1) убедиться, что найденное частное решение удовлетворяет начальному условию;
2) проверить, что частное решение вообще удовлетворяет дифференциальному уравнению.
Пример 5
Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию  .
.
Выполнить проверку.
Решение:
Сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы. Разделяем переменные:



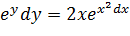
Интегрируем уравнение:

Интеграл слева – табличный

интеграл справа решаем методом замены переменной

Общий интеграл

Логарифмируем обе части. Поскольку они положительны, то знаки модуля излишни:

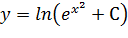
Найдем частное решение, соответствующее заданному начальному условию 
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы

Проверка:
Сначала проверим, выполнено ли начальное условие 

Теперь проверим, а удовлетворяет ли вообще найденное частное решение дифференциальному уравнению. Находим производную:

Смотрим на исходное уравнение:

– оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал dy


Подставим найденное частное решение

и полученный дифференциал в исходное уравнение



Используем основное логарифмическое тождество




Получено верное равенство, значит, частное решение найдено правильно.
Пример 6
Найти общий интеграл уравнения

ответ представить в виде 