Лекция 2 Законы симметрии в кристаллах на примере кубической сингонии
Андрей Владиславович Вишневский
Кристаллы разных веществ в своей основе имеют минимальные строительные элементы, кирпичики, которые соединяясь друг с другом в объёмное тело образуют кристалл. При нестесненном росте и умеренных величинах пересыщения образуются плоскогранные кристаллы.
Кристаллы имеют различные параметры этого минимального строительного кирпичика - элементарной ячейки. Различия имеются в их размере, типе частиц и форме. Для каких-то веществ элементарная ячейка имеет форму косого параллелепипеда, боковые грани которого являются косыми параллелограммами и неперпендикулярны основанию, для других это прямой параллелепипед, боковые грани которого представляют собой прямоугольники, для третьих она имеет правильную кубическую форму, в которой все грани одинаковы и перпендикулярны основаниям.
Здесь кроется фундаментальная разницу между системами расположения частиц в структуре кристалла - его кристаллической решетке. Частиц, расположение которых друг относительно друга увязано определёнными законами, которые называются законами симметрии.
Основные параметры любой элементарной ячейки можно описать тремя базовыми векторами, её базисом. Это векторы a, b и c и углы α, β и γ соответственно. Если a не равно b и не равно c, то такие структуры относятся к низшей категории симметрии. И здесь есть три варианта соотношений углов α, β и γ, которые дают три, так называемых сингонии (от греческого "син" - "сходно" и "гон" - "угол"): триклинную, моноклинную и ромбическую. Если a равно b, но не равно c, то такие кристаллы относят к средней категории. Здесь выделяют тетрагональную, тригональную и гексагональную сингонии. И, наконец, когда a равно b и c, и все углы прямые. Такие кристаллы относят к высшей категории, и в ней всего одна сингония - кубическая. У неё есть несколько видов, но объект нашего исследования, квасцы, относится к максимально высокосимметричному из них.
|
|
Но, что же такое симметрия? Базовыми понятиям в этой области являются ось симметрии и плоскость симметрии. В обычной жизни мы чаще всего имеем дело с плоскостной симметрией – здесь всё – от самолёта, до внешнего облика нашего с вами тела. В биологии такую симметрию называют билатеральной, хороший пример тут - лист дерева.
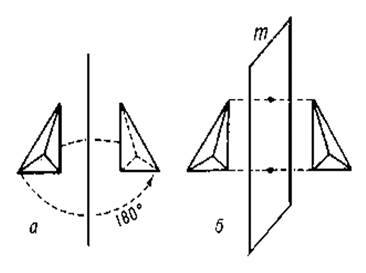
Действие оси симметрии второго порядка и плоскости симметрии
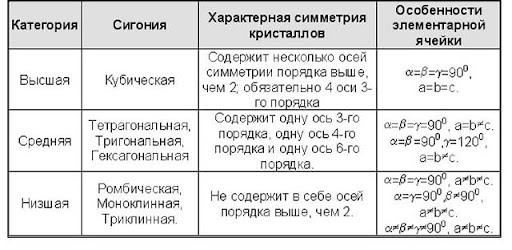
Воображаемая плоскость, разделяющая предмет так, что две половины выглядят как зеркальные отражения друг друга, называется плоскостью симметрии и часто обозначается латинской буквой Р. У самолета или человеческого лица имеется только одна плоскость симметрии, однако множество окружающих нас вещей имеет несколько плоскостей. Например, у самого примитивного прямоугольного стола их две, а у табурета с квадратным сидением уже целых четыре. Интересно и важно, что все четыре плоскости симметрии в этих случаях пересекаются по одной линии.
Второй основной элемент симметрии – ось. Осевая симметрия также распространена в природе, но в сложноустроенных биологических объектах встречается гораздо реже. Хороший пример здесь – цветы. У разных растений они могут иметь разную осевую симметрию.
|
|
Осью симметрии называется воображаемая линия при повороте вокруг которой на определенный угол форма предмета совмещается сама с собой. Этот угол может быть, например, 180°. В этом случае при повороте на 360° предмет совмещается с собою дважды. Такая ось называется осью симметрии второго порядка и обозначается L2 или чечевицеобразным значком. Если совмещение происходит три раза, при повороте на 120°, тогда это ось симметрии третьего порядка и обозначается L3 и треугольным значком. При четырёхкратном совмещении угол поворота вокруг оси составляет 90°, такая ось четвертого порядка обозначается как L4 или квадратным значком. Ось пятого порядка с углом поворота на 72° для кристаллических веществ не характерна, хоть и встречается в биологических объектах, мы ее рассматривать не будем. И максимальная для кристаллов ось – шестого порядка - с углом поворота в 60°, обозначающаяся L6 и шестисторонним многогранником.
Интересно взаимодействие элементов симметрии между собой. Две пересекающиеся плоскости дают ось симметрии. Однако сама по себе ось симметрии вполне может существовать и без образующих её плоскостей.
Вспомним плоскостную симметрию стола. Две плоскости симметрии пересекаются, в результате линия их пересечения даёт ось симметрии второго порядка. Действительно, если развернуть такой стол на 180° он совместится сам с собой. При повороте ещё на 180° придёт в исходное положение. Итак, пересечение плоскостей симметрии даёт ось с углом поворота в два раза большим, чем угол между плоскостями. Пересечение плоскостей симметрии табурета даёт угол в 45°, это пересечение даст нам ось симметрии четвертого порядка с углом поворота в 90°.
|
|
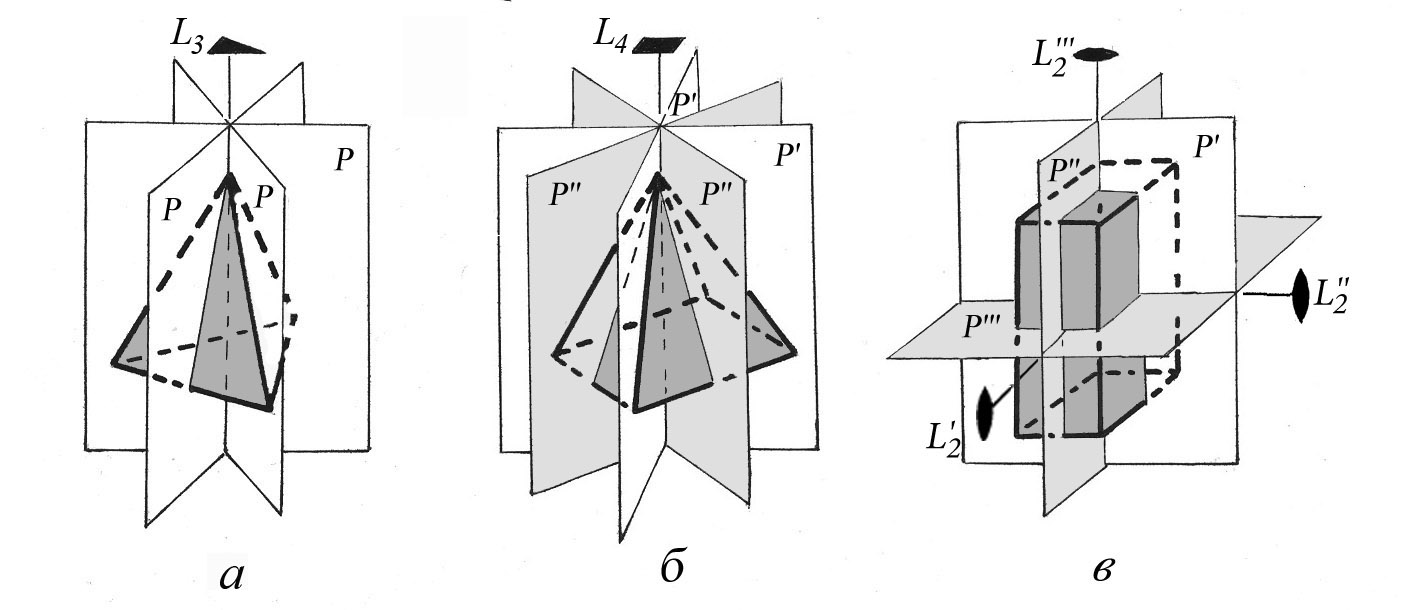
Плоскости и оси симметрии у некоторых фигур. а – тригональная пирамида, б – тетрагональная пирамида, в – ромбическая призма. L – оси симметрии разного порядка, P - плоскости
В кристаллах низшей категории максимально может присутствовать осевая симметрия второго порядка. Не более. Количество плоскостей симметрии ограничено тремя, пересекающимися под углом в 90°. Это реализуется в ромбической сингонии – такие кристаллы наиболее высокосимметричные в низшей категории. Примером кристаллического вещества с такой симметрией является распространенный минерал оливин. Его кристаллы чаще всего имеют короткопризматический облик. Плоскости симметрии пересекаются под углом в 90°, линии пересечения плоскостей являются осями второго порядка. Одно из наиболее распространённых в хозяйстве монокристаллических веществ – сахар также относится к низшей категории, но не к ромбической, а к моноклинной сингонии, и не имеет плоскостей симметрии, а только одну ось второго порядка. В этом можно убедиться, внимательно рассматривая кристаллики сахара под увеличением.
В кристаллах средней категории из-за того, что векторы a и b равны, автоматически появляется ось третьего, четвертого или шестого порядка. Такую симметрию имеют распространенные минералы, например, кварц – оксид кремния, слагающий значительную долю пород земной коры: гнейсов, сланцев, гранитов и песчаников, и кальцит – карбонат кальция, из которого состоят такие горные породы как известняк и мрамор.
Нам же, в первую очередь интересна высшая категория. Одной из базовых фигур, которая обладает максимальным количеством, или как ещё говорят, максимальным набором элементов симметрии, является куб. Рассмотрим этот максимальный набор на его примере. Начнем с осей симметрии. У куба, или, иначе, гексаэдра имеется 6 одинаковых квадратных граней, которые пересекаются под прямым углом, и у каждой грани, таким образом, имеется противолежащая её параллельная грань. Квадрат имеет тетрагональную (четверную) симметрию - при повороте на 90° он приходит в тождественное положение. Таким образом, через центр каждой грани проходят оси симметрии четвертого порядка, всего таких осей три, и пересекаются они под прямым углом. Кроме того, каждая из этих осей является линией пересечения четырёх плоскостей симметрии, пересекающихся под углом 45°, что также легко проверить, или можно снова вспомнить табурет.
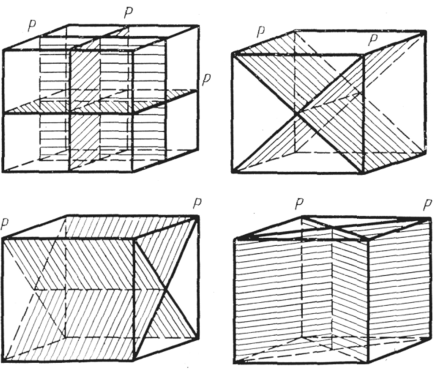
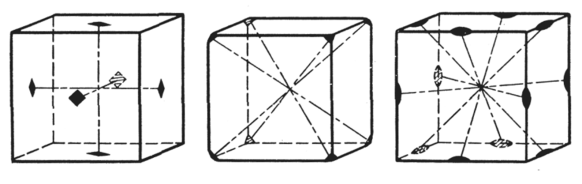
Ориентировка осей и плоскостей симметрии у куба
Сколько же таких плоскостей имеется в сумме? Во-первых, часть из этих плоскостей – координатные. Каждая из них участвует в образовании двух осей четвёртого порядка, которые, совпадают с базисом кубической сингонии. Всего этих плоскостей – три. Во-вторых, на каждой грани куба мы видим кроме двух координатных плоскостей, по две диагональных плоскости симметрии. Всего таких плоскостей шесть – по две плоскости связаны с каждой из трёх координатных осей. Таким образом, мы получаем девять плоскостей симметрии.
Мы видим, что есть плоскости, которые пересекаются друг с другом, и помним, что по законам кристаллографии, в этом случае появляется ось симметрии, совпадающая с линией пересечения плоскостей, и углом поворота в два раза меньше, чем угол между этими плоскостями. Во-первых, это пересечения четырех плоскостей – двух координатных и двух диагональных – здесь образуются уже отмеченные оси четвёртого порядка. Во-вторых, имеются пересечения координатных плоскостей симметрии с диагональными. Они пересекаются в центрах рёбер куба. Всего таких пересечений – шесть, так как у куба 12 попарно параллельных ребер. Угол между плоскостями в этом случае составляет 90°, здесь находятся оси второго порядка с углом поворота 180°. И, наконец, самое интересное. Пересекающиеся диагональные плоскости дают ось, проходящую по так называемой телесной диагонали куба, у куба 8 вершин, соответственно имеются 4 телесные диагонали. Диагональные плоскости симметрии пересекаются под углом 60°, что даёт 4 оси с поворотом в 120° - это оси третьего порядка.
Зафиксируем важный момент – все оси симметрии пересекаются в центре симметричной фигуры, в данном случае – куба.
Итак, мы вывели максимальный набор элементов симметрии для куба. Это три оси четвертого порядка, четыре оси третьего порядка, шесть осей второго порядка и девять плоскостей симметрии. 3L44L36L29PC. Вот так может выглядеть этот набор элементов симметрии в записи. При взаимодействии плоскости симметрии с перпендикулярной ей чётной осью появляется центр симметрии, действие которого дублируется осями и плоскостями, так что в упрощенной модели можно его не рассматривать отдельно.
Такую же симметрию имеют и другие базовые формы кубической сингонии – октаэдр и ромбододекаэдр.
Октаэдр – правильный восьмигранник. Его грани являются равносторонними треугольниками. У октаэдра выходы осей четвертого порядка находятся на вершинах, там, где сходятся вместе четыре грани. Оси третьего порядка перпендикулярны граням, а оси второго порядка, как и у куба, выходят в центрах рёбер. Так же, как и куба, у октаэдра двенадцать попарно параллельных рёбер.
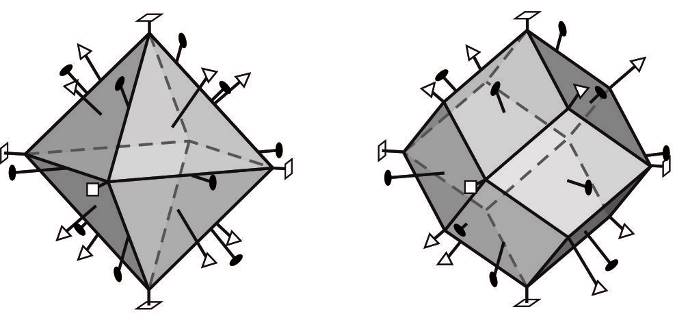
Октаэдр и ромбододекаэдр с осями симметрии. У октаэдра оси третьего порядка совпадают с нормалями к граням, а ромбододекаэдра – оси второго порядка.
Ромбододекаэдр – правильный двенадцатигранник с ромбическими гранями. Стоит заострить здесь внимание на форме, так как существует еще менее симметричный пентагондодекаэдр, с пятиугольными гранями. Оси четвертого порядка у ромбододекаэдра, так же, как и у октаэдра – выходят на острых вершинах, там, где сходятся с одинаковым углом четыре грани. Оси третьего порядка выходят в местах, где с одинаковым углом сходятся по три грани. А где же выходят оси второго порядка? В кубе и октаэдре они опирались о 12 рёбер, здесь же на месте рёбер находятся ромбические грани и их тоже 12. Оси второго порядка перпендикулярны этим граням и проходят через их центр.
Для удобства отображения трёхмерных фигур на бумаге или экране используются проекции различного типа - стереографические и гномостереографические. Сейчас мы не будем подробно останавливаться на их особенностях и свойствах, обозначим положение и действие элементов симметрии на проекции и рассмотрим частный случай для максимального набора элементов симметрии кубической сингонии.
Для перенесения на плоскость элементов симметрии используются сферические проекции, где плоскость проецирования проходит через центр сферы – точку, в которую виртуально помещается проецируемый кристалл и в которой, как мы помним, пересекаются все оси симметрии. Две координатные оси симметрии четвертого порядка, которые называются х и у при этом оказываются лежащими в экваториальной плоскости. Третья ось z ориентирована перпендикулярно экваториальной плоскости, то есть под прямым углом к плоскости проекции (вертикально) и проецируется в центр. Не будем пока рассматривать все остальные элементы симметрии, посмотрим, как работают оси четвёртого порядка. Для этого нужно нанести на проекцию грани кристалла.
Грани наносятся на проекцию способом, сходным с проецированием осей. К граням строятся нормали – линии, перпендикулярные им и проходящие через центр сферы. Так как плоскость проецирования разрезает сферу на два полушария, некоторые грани окажутся в нижней полусфере, некоторые в верхней. Первые на проекциях обозначают кружками, вторые – крестиками. Грани, попадающие на экватор, который называется большим кругом обозначаются кружочками. Нанесем на проекцию грань с индексом 100 – это грань куба, которая параллельна осям y и z. Нормаль к этой грани параллельна оси х. Точка оказывается на большом круге, на его пересечении с осью. Далее действуем вертикальной осью четвертого порядка. Симметричным преобразованием этой осью – поворотом на 90° вокруг неё, получаем ещё три грани куба, лежащие на большом круге. Эти грани имеют индексы 0-10 -100 и 010 соответственно.
Необходимо получить еще две грани с индексами 001 и 00-1. Обратите внимание что проекция нормали к одной из граней находится в нижней полусфере и значение третьего индекса отрицательное
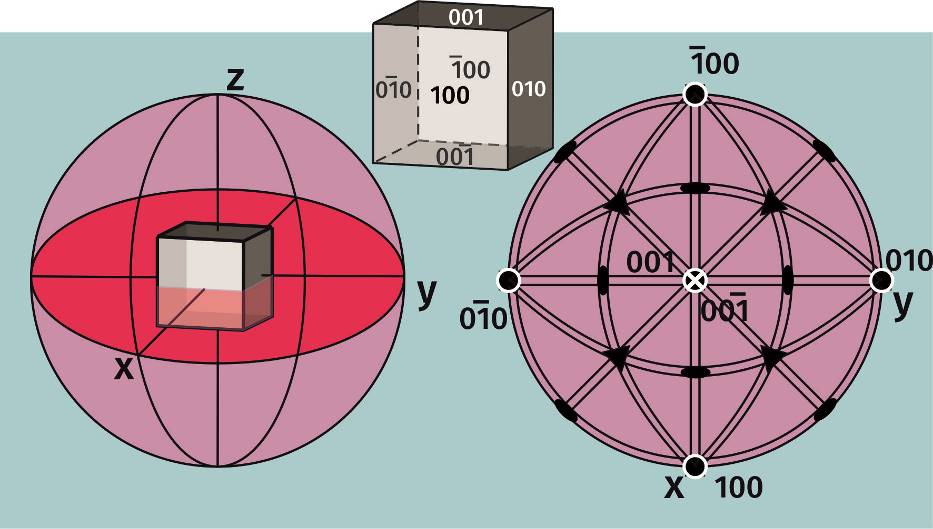
Куб в центре сферы проекции, плоскость проецирования выделена красным. Справа – круг проекции с нанесенными элементами симметрии и стереографическая проекция граней куба с обозначенными кристаллографическими индексами.
Получить с помощью элементов симметрии эти плоскости (грани) можно действуя другими координатными осями. Например, ось четвертого порядка, ориентированная по координатной оси y также имеет угол поворота 90°, и своим действием будет образовывать четыре грани. Две из них с поворотом 180° уже имеются, ещё две появятся на северном и южном полюсах сферы, они будут проецироваться точно в центр круга проекции – та, что на северном (в верхней полусфере) – кружочком, а вторая – крестиком. Таким образом, имеем шесть граней - проекцию куба. Аналогичным образом можно было бы действовать осью четвертого порядка, ориентированной по оси х.
Здесь мы подошли к важному термину: простая форма. Простая форма – фигура, все грани которой связаны симметричными преобразованиями, и поэтому имеют одинаковую форму и размер. Иначе говоря – это совокупность граней, выводящихся друг из друга определённым набором элементов симметрии. В нашем случае, например, это куб. Всего, во всех сингониях и видах симметрии насчитывается 47 геометрических простых форм. Самая простая из простых форм – моноэдр, который представляет собой одиночную плоскость, и встречается в некоторых видах симметрии низшей и средней категории.
В примитивном виде триклинной сингонии элементы симметрии отсутствуют вовсе, и любая точка в любом положении на проекции не может быть размножена никаким действием. То есть, если мы зададим, например, в программе для построения моделей кристаллов, примитивный вид триклинной сингонии, но вручную сделаем a, b и c одинаковыми и углы α, β и γ по 90°, то расположив, грани, а соответственно и точки на проекции таким же образом как для куба, получим псевдокубическую форму многогранника. Но на самом деле это будут шесть моноэдров, дающих кубическую форму.
Этот приём используется для построения моделей неидеальных кристаллов, о которых мы поговорим следующем видео. Ведь не каждая грань простой формы растет с одной скоростью и в одних условиях. Таким же способом можно построить и трёхмерную модель, максимально приближенную к выращенному кристаллу, что также можно использовать в нашем проекте.
Нанесем теперь на проекцию плоскости симметрии. При пересечении любой плоскости с проекционной сферой получаются окружности одинакового радиуса. Это всё потому, что по умолчанию все плоскости проходят через центр сферы. Однако ориентировка этих окружностей будет различна.
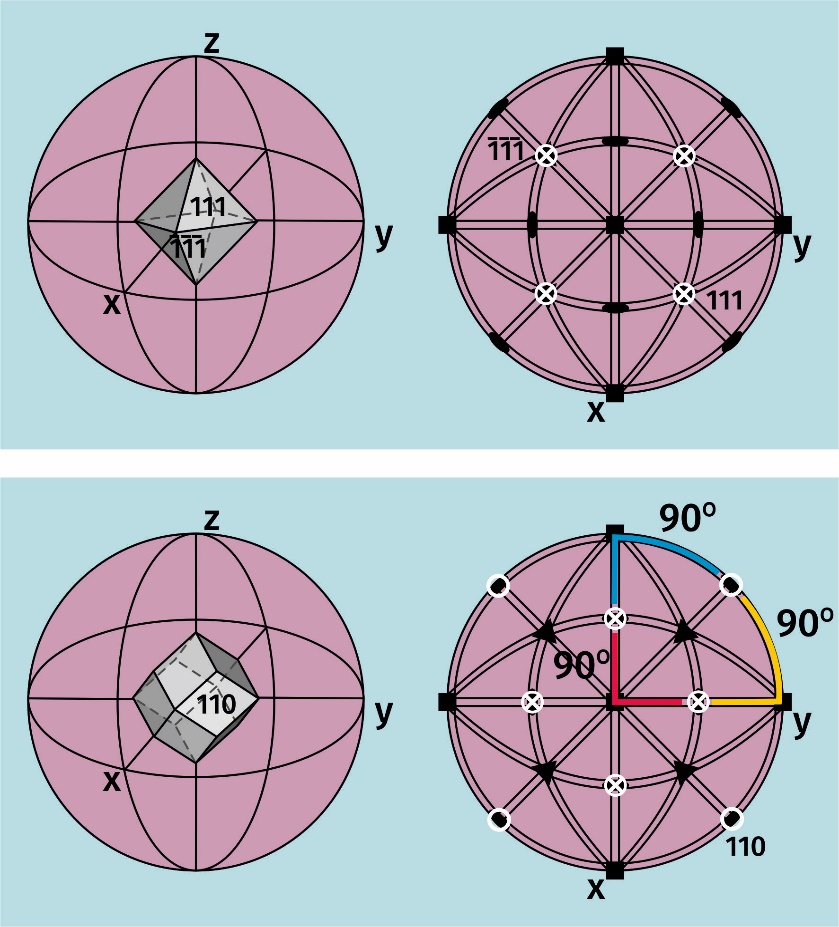
Стереографические проекции октаэдра и ромбододекаэдра
Если такая окружность ориентирована вертикально, то её проекция будет прямой линией, проходящей через центр, если горизонтально, то она будет совпадать с большим кругом. Это наши координатные плоскости.
Диагональные плоскости симметрии, ориентированные вертикально располагаются очевидным образом на проекции – под углом в 45° относительно координатных.
Немного сложнее с остальными диагональными плоскостями. Условно говоря, на диаметр круга плоскости проекции опирается и проецируется дуга в 180° в верхней полусфере и 180° в нижней. Геометрический смысл этой дуги – та же окружность на сфере проекции, которую мы переносим на плоскость. Поэтому на такой проекции наклонные плоскости симметрии выглядят дугами, проходящими через центры радиусов по координатным направлениям.
С нанесением осей симметрии второго и третьего порядка теперь никаких проблем не будет. Мы уже определились с их положением и образованием при взаимодействии соответствующих плоскостей симметрии.
Нанесем на проекцию оси третьего порядка. Они будут находится посреди каждого из четырёх квадрантов круга проекции, в месте пересечения трёх диагональных плоскостей. И, наконец, оси второго порядка, находятся на пересечении координатных и диагональных плоскостей.
Таким образом, на проекции оказались нанесены все элементы симметрии планаксиального вида кубической сингонии. Плюс ещё центр симметрии, конечно.
Проверим работу элементов симметрии на примере куба. Как и в первый раз, возьмем грань 100. Действием оси третьего порядка можем перенести её в три эквивалентные позиции – 001 и 010. Угловые расстояния между этими позициями одинаковые – по 90 градусов. Теперь, например, отразим точку 001 горизонтальной плоскостью симметрии в нижнюю полусферу – получим грань 00-1. А остальные грани отразим вертикально ориентированной диагональной плоскостью. В итоге получим шесть граней куба.
Что же с октаэдром и ромбододекаэдром? А всё теперь довольно просто. Нормаль к грани октаэдра совпадает с осью третьего порядка, соответственно будет четыре точки в верхнем полушарии и четыре в нижнем. Индекс базовой грани октаэдра – 111, а противолежащей -1-1-1, эти плоскости отсекают равные отрезки на всех трех координатных осях Никакие элементы симметрии более размножить эти точки не могут. Грани ромбододекаэдра «нанизаны» на оси второго порядка. Индекс базовой грани – 110. Четыре грани располагаются на большом круге, а ещё восемь в эквивалентных позициях на пересечении координатных и диагональных плоскостей. Вы можете самостоятельно потренироваться выводить положение точек этих простых форм с помощью действия разных элементов симметрии, а также попробовать другие возможные позиции, которых в этом виде симметрии имеется еще четыре, это ещё четыре простые формы.
Итак, каждый кристалл обладает своим внутренним устройством – определенной кристаллической решеткой. Симметрия расположения частиц в ней подчиняется строгим законам. Внешняя форма кристаллов является отражением их структуры, и может быть описана с помощью элементов симметрии. Кристаллы квасцов принадлежат к планаксиальному, наиболее высокосимметричному виду кубической сингонии, базовыми формами для которой являются куб, октаэдр и ромбододекаэдр.