12.11.2021
Урок 1.Тема: «Исследование линейных и квадратичных функций»
Задание №1. Запишите схему исследования функции (если нет)
Схема исследования функции
Область определения функции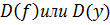 
| Для всех видов функций пишем D(f): R, за исключением дробей, корней, логарифмов и тангенса (котангенса) | |
| 2. | Четность | В функцию вместо x подставить (-x) и проверить, какие получатся знаки: Все знаки сохранились: четная; Все изменились - нечетная; некоторые сохранились – ни четная, ни нечетная |
| 3. | Периодичность | Только для тригонометрических функций |
| 4. | Точки пересечения с осями координат | С осью Ох: подставить вместо у=0 С осью Оу: подставить вместо х=0 |
| 5. | Промежутки знакопостоянства | Решить неравенства y>0, y<0 |
| 6. | Промежутки монотонности (возрастание и убывание) | |
| 7. | Экстремумы функции |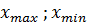 
|
| 8. | Наибольшее и наименьшее значения функции |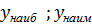 
|
| 9. | Множество значений функции |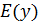 
|
Задание №2. Рассмотрите примеры исследования линейной и квадратичной функции. Разберите их и запишите в тетради.
Пример №1. f(x) = 5-2х
1. D(f): R
2. Четность
f(-x)=5-2 ∙(-x)=5+2x – функция ни четна, ни нечетна (некоторые знаки сохранились, а некоторые изменились)
3. Непериодическая.
4. С осью Ох: у=f(x) = 0, 5-2x=0, -2x = -5, x = 2,5 (2,5;0)
С осью Оу: х=0, у=5-2·0=5 (0; 5)
5. f(x)>0: 5-2x>0, -2x>-5, x<2,5.
f(x)>0 при x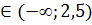 
f(x)<0 при x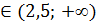 
Остальные свойства запишем по графику, построив его. Графиком данной функции является прямая, для построения которой нужно знать 2 точки.
| x | 0 | 2 |
| y | 5 | 1 |
6. Функция убывает на всей числовой прямой, т.к. k=-2<0
7. Точек экстремума нет
8. Наибольшего и наименьшего значения нет
9. E(f): R
Пример №2. y = 8 - 2x – x2.
1. D(f): R
2. Четность
f(-x)=8-2·(-x)-(-x)2 =8+2x –x2 – функция ни четна, ни нечетна (некоторые знаки сохранились, а некоторые изменились)
3. Непериодическая.
4. С осью Ох: у= f(x) = 0, 8– 2x – x2=0,
Перепишем уравнение в виде – x2-2х+8=0, D=(-2)2-4∙(-1)∙8 = 36; x1=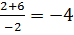 
; x2= 
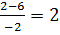, получаем две точки (-4;0) и (2; 0)
С осью Оу: х=0; 8-2·0-02=8, получаем точку (0; 8)
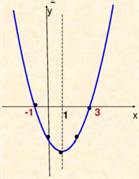
Графиком данной функции является парабола, ветви которой направлены вниз, так как а=-1<0.(перед х2 знак минус)
Найдем вершину параболы.
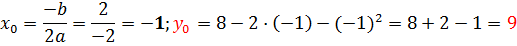
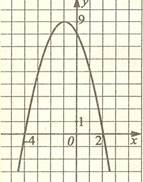
Строим параболу по точкам (по рисунку запишем остальные свойства)
| x | -4 | -2 | -1 | 0 | 2 |
| y | 0 | 2 | 9 | 2 | 0 |
5. f(x)>0: при x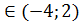 
f(x)<0 при x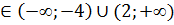 
6. Функция возрастает на (-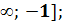 
убывает на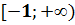 
7. х = -1 - точка максимума
8. Наименьшего значения нет; унаиб.=9
9. E(f):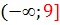 
Примечание: Если у параболы ветви направлены вверх, то промежутки возрастания и убывания поменяются местами, не будет наибольшего значения, будет только
унаим., будет точка минимума (точек максимума нет)
Урок 2.Тема: «Исследование рациональных функций. Непрерывность»
Задание 1. Изучите тему и разберите примеры УСТНО (ничего конспектировать не нужно)
Многие рациональные функции содержат переменную х в знаменателе, а значит нельзя сказать, что областью определения таких функций являются все действительные числа. В этом случае из множества R нужно исключить точки, в которых знаменатель обращается в нуль. Такие точки и являются точками разрыва функции. Примеры таких функций:
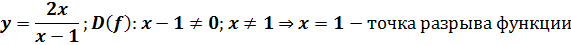
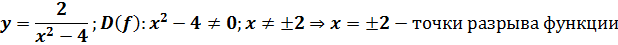
Такие функции не являются непрерывными, у них нельзя построить график, не отрывая руки от тетради(ниже приведены графики функций, которые не являются непрерывными)
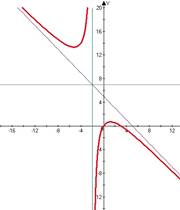
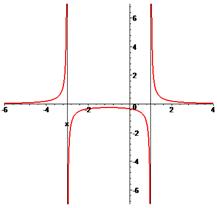
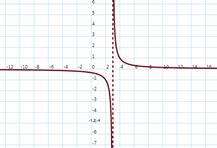
1. Точка разрыва функции – это точка, около которой значения функции совершают скачок (конечный или бесконечный)
2. Функция называется непрерывной на промежутке, если у нее нет на этом промежутке точек разрыва.
3. Функция называется гладкой на промежутке, если в каждой точке ее графика можно однозначно провести касательную.
4. Угловые точки – точки, в которых нарушается гладкость (это точки разрыва функции, а также точки, в которых график образует угол)
5. Выпуклость функции. Наглядным свойством графика функции на некотором промежутке является его выпуклость, которая может быть направлена как вверх, так и вниз. Точка, в которой меняется характер выпуклости, называется точкой перегиба функции. Если в этой точке провести касательную к графику функции, то по одну сторону от точки перегиба график функции расположен выше касательной, а по другую – ниже.
6. Асимптота графика функции – прямая, к которой неограниченно приближаются точки графика функции при их удалении от начала координат. Асимптоты бывают вертикальные, горизонтальные и наклонные.
Задание. По графику функции, изображенному на рисунке определите: непрерывность функции, точки разрыва, угловые точки, точки перегиба, характер выпуклости, асимптоты.
ПРИМЕР №1.
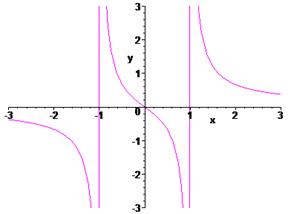
Решение.
1. Данная функция непрерывна на (-∞; -1)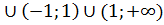 
.
2. Точки разрыва х = -1, х =1.
3. Функция является гладкой на (-∞; -1) .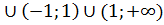
4. Угловые точки х = -1, х =1.
5. х=0 – точка перегиба.
6. х = -1, х =1- вертикальные асимптоты.
ПРИМЕР №2.
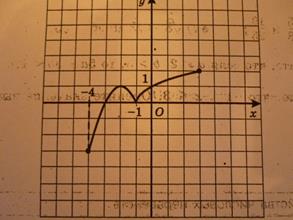
| 1. Данная функция непрерывна на (-4; 3  .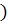
2. Точек разрыва нет.
3. Функция не является гладкой, т.к. в точке х= -1 нельзя однозначным образом провести касательную.
4. х= -1 – угловая точка.
5. Точек перегиба нет.
6. Асимптот нет.
|