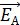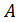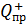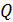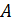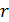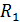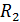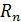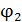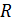Электростатическое поле (ЭСП)
Напряженность электрического поля (ЭП)
Закон Кулона: сила взаимодействия двух неподвижных точечных электрических зарядов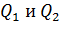 
определяется формулой
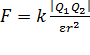; (3)
где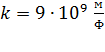 
– коэффициент пропорциональности; 
– диэлектрическая проницаемость среды; 
– расстояние между зарядами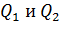
Напряженность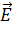 
– силовая характеристика ЭП, равная отношению:
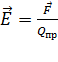, (4)
где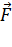 
– сила, действующая на положительный пробный заряд 
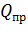, помещенный в ту точку пространства, где определяют напряженность ЭП. Из определительной формулы (4) следует, что в данной точке ЭП вектор 
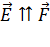. Поэтому для определения направления вектора напряженности в выбранной точке 
ЭСП в эту точку мысленно помещают положительный пробный заряд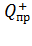 
и с помощью закона Кулона определяют направление силы 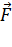и 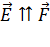(рис. 2).
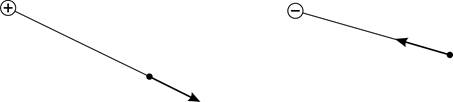
Рис. 2 |
Напряженность поля, созданного точечным зарядом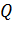 
в точке , находящейся на расстоянии от заряда (см. рис. 2), согласно формуле (4) с учетом закона Кулона (3), определяется следующей формулой:
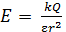. (5)
Принцип суперпозиции ЭСП: напряженность 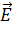результирующего поля, созданного системой зарядов, равна геометрической сумме напряженностей 
полей, создаваемых в данной точке каждым i-тым зарядом (рис. 3):
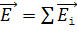. (6)
Здесь сумма векторов!!!
Потенциал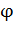 
– энергетическая характеристика ЭСП в данной точке поля:
(14)
где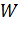 
– потенц. энергия пробного заряда 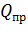, помещ. в данную точку ЭСП.
В поле точечного заряда потенциал точки, нах. на расстоянии от заряда:
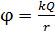, (15)
где 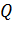– заряд, создающий поле.
Потенциал 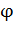– алгебраическая величина, его знак равен знаку заряда 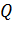, создающего поле (см. формулу (15)). Потенциал ЭСП, созданного в данной точке несколькими зарядами равен алгебраической сумме потенциалов 
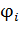полей всех заряженных тел в этой точке:
|
|
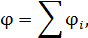
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Сила тока. Плотность тока. Сопротивление проводника
Сила тока 
, или ток, по определению
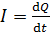, (1)
где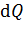 
– бесконечно малый заряд, прошедший через поперечное сечение проводника за время 
.
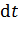Сила постоянного тока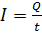 
.
Сопротивление проводника длиной 
и поперечным сечением 
:
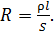(3)
Здесь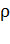 
– удельное сопротивление материала проводника. При увеличении температуры металла его удельное сопротивление растет линейно:
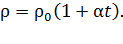(4)
Здесь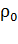 
– уд. сопротивление проводника при 
; 
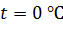– температура проводника по шкале Цельсия;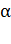 
– температурный коэф. сопротивления (ТКС) металла.
Сопротивление последовательно соединенных проводников (рис. 38):
Рис. 38 |
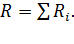(5)
Сопротивление параллельно соединенных проводников (рис. 39):
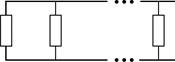
Рис. 39 |
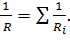(6)
Закон Ома. Правила Кирхгофа
Закон Ома для однородного участка цепи (не содержащего источника тока: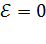 
) (рис. 40 б):
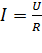. (8)
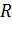– сопротивление участка, 
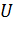– напряжение на участке цепи.
|
Для замкнутой цепи закон Ома:
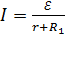, (9)
где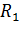 
– сопр. внешнего участка, – внутреннее сопрот. источника тока.
Правила Кирхгофа используются для расчета разветвленных цепей, содержащих несколько замкнутых контуров.
Первое правило – алгебраич. сумма токов, сходящихся в узле, равна нулю:
|
|
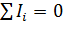. (11)
Здесь положительными считают токи, входящие в узел (приносящие заряд), а отрицательными – выходящие из узла (уносящие заряд).
Второе правило – в любом замкнутом контуре, в разветвленной эл цепи, алгебраическая сумма произведений токов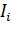 
на сопротивления 
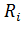на всех участках контура равна алгебраической сумме ЭДС в этом контуре:
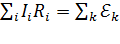. (12)
Работа и мощность тока. Закон Джоуля – Ленца
Работа по переносу заряда при протекании тока в электрической цепи, совершаемая за время : 
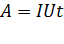, (13)
где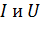 
– сила тока и напряжение на участке цепи.
Мощность тока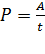 
; с учетом закона Ома (7) получают след. формулы:
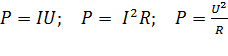. (14)
Закон Джоуля – Ленца: количество теплоты 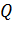, выделяемое в участке цепи за время , определяется следующими формулами:
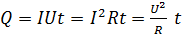. (15)