Длина волны де-Бройля для движущейся частицы:
а) 

б) релятивистский случай  ,
,

Связь длины волны де-Бройля с кинетической энергией частицы:
а) 

б) релятивистский случай

где  – энергия покоя частицы.
– энергия покоя частицы.
Фазовая скорость микрочастицы

где 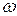 – циклическая частота;
– циклическая частота;  – волновое число.
– волновое число.
Групповая скорость

Соотношение неопределенностей:
а) для координаты и импульса частицы

где  – неопределенность проекции импульса частицы на оси
– неопределенность проекции импульса частицы на оси  ;
;  – неопределенность ее координаты;
– неопределенность ее координаты;
б) для энергии и времени

где  – неопределенность энергии данного квантового состояния;
– неопределенность энергии данного квантового состояния;  – время пребывания системы в этом состоянии.
– время пребывания системы в этом состоянии.
Одномерное нестационарное уравнение Шредингера

где  –мнимая единица;
–мнимая единица;  – масса частицы;
– масса частицы;  – волновая функция, описывающая состояние частицы;
– волновая функция, описывающая состояние частицы;  – потенциальная энергия частицы в силовом поле.
– потенциальная энергия частицы в силовом поле.
Волновая функция, описывающая одномерное движение свободной частицы
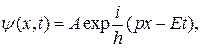
где  – амплитуда волны де-Бройля;
– амплитуда волны де-Бройля;  – импульс частицы;
– импульс частицы;  – энергия частицы.
– энергия частицы.
Одномерное уравнение Шредингера для стационарных состояний

где  – полная энергия частицы;
– полная энергия частицы;  – потенциальная энергия;
– потенциальная энергия;  – координатная часть волновой функции.
– координатная часть волновой функции.
Для трехмерного случая уравнение Шредингера для стационарных состояний имеет вид

где  – оператор Лапласа.
– оператор Лапласа.
Вероятность обнаружить частицу в интервале от  до
до 

где  – плотность вероятности.
– плотность вероятности.
Вероятность обнаружить частицу в интервале от  до
до 

Собственные значения энергии  частицы, находящейся в бесконечно глубокой потенциальной «яме»
частицы, находящейся в бесконечно глубокой потенциальной «яме»

где  – ширина «ямы».
– ширина «ямы».
Волновая функция для частицы, находящейся в одномерной глубокой потенциальной яме, имеет вид

Собственные значения энергии  электрона в водородоподобном ионе
электрона в водородоподобном ионе

где 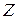 – зарядовое число ядра иона;
– зарядовое число ядра иона;  – заряд электрона;
– заряд электрона;  – электрическая постоянная;
– электрическая постоянная;  – постоянная Планка;
– постоянная Планка;  – главное квантовое число
– главное квантовое число 
Орбитальный момент импульса и магнитный момент электрона

где  – магнетон Бора.
– магнетон Бора.
Проекция орбитального момента импульса и магнитного момента на направление внешнего магнитного поля

где  – магнитное квантовое число, которое принимает значения
– магнитное квантовое число, которое принимает значения  магнетон Бора.
магнетон Бора.
Спиновый момент импульса и магнитный момент электрона

где  – спиновое квантовое число.
– спиновое квантовое число.
Правила отбора для квантовых чисел 

| Задание 3.1 | |||
| Групповая скорость волны де-Бройля… | |||
| Варианты ответов: | |||
| 1) | равна скорости сета в вакууме | 2) | не имеет смысла как физическая величина |
| 3) | больше скорости сета в вакууме | 4) | зависит от квадрата длины волны |
| 5) | равна скорости частицы |
| Задание 3.2 | |||
Два источника излучают свет с длинами волн 375 нм и 750 нм. Отношение импульсов фотонов  равно… равно…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | |
| 3) | 0,4 | 4) |
| Задание 3.3 | |||
Если протон и нейтрон двигаются с одинаковыми скоростями, то отношения их длин волн де-Бройля  равно… равно…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | |
| 3) | 4) |
| Задание 3.4 | |||
| Если частицы имеют одинаковую длину волны де-Бройля, то наименьшей скоростью обладает… | |||
| Варианты ответов: | |||
| 1) | протон | 2) | позитрон |
| 3) |  -частица -частица
| 4) | нейтрон |
| Задание 3.5 | |||
| Если длина волны де-Бройля частиц одинакова, то наибольшей скоростью обладает… | |||
| Варианты ответов: | |||
| 1) | нейтрон | 2) | электрон |
| 3) |  -частица -частица
| 4) | протон |
| Задание 3.6 | |||
Электрон локализован в пределах  . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка  а масса электрона а масса электрона  неопределенность скорости неопределенность скорости  (в м/с) равна… (в м/с) равна…
| |||
| Варианты ответов: | |||
| 1) | 8,7 | 2) | 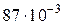
|
| 3) | 0,115 | 4) |
| Задание 3.7 | |||
Согласно принципу неопределенности облако свободного электрона, первоначально локализованное в области диаметром  м, за тысячную долю секунды расплывется до размера … Принять м, за тысячную долю секунды расплывется до размера … Принять   . .
| |||
| Варианты ответов: | |||
| 1) | 1 мкм | 2) | 1 мм |
| 3) | 1 м | 4) | 1 км |
| Задание 3.8 | |||
Облако свободного электрона первоначально имеет размер атома  м. Электронное облако расплывается до размеров футбольного мяча (0,1м) за время порядка… Принять м. Электронное облако расплывается до размеров футбольного мяча (0,1м) за время порядка… Принять  
| |||
| Варианты ответов: | |||
| 1) | 1 с | 2) |  с с
|
| 3) |  с с
| 4) |  с с
|
| 5) |  с с
|
| Задание 3.9 | |||
Протон локализован в пределах  . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка  масса протона масса протона  неопределенность скорости неопределенность скорости  (в м/с) равна… (в м/с) равна…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 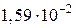
|
| Задание 3.10 | |||
Положение пылинки массой  можно установить с неопределенностью можно установить с неопределенностью  . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка  неопределенность скорости неопределенность скорости  (в м/с) будет не менее… (в м/с) будет не менее…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 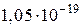
| 4) | 
|
| Задание 3.11 | |||
Время жизни атома в возбужденном состоянии  . Учитывая, что постоянная Планка . Учитывая, что постоянная Планка  ширина энергетического уровня (в эВ) составляет не менее… ширина энергетического уровня (в эВ) составляет не менее…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 3.12 | |||
Время жизни возбужденного состояния молекулы равно  с. Согласно принципу неопределенности диапазон частот, излучаемых молекулой при радиационном распаде этого состояния, составляет… с. Согласно принципу неопределенности диапазон частот, излучаемых молекулой при радиационном распаде этого состояния, составляет…
| |||
| Варианты ответов: | |||
| 1) | 1 МГц | 2) | 0,01 МГц |
| 3) | 100 МГц | 4) | 10 МГц |
| 5) | 0,1 МГц |
| Задание 3.13 | |||
| Интервал частот, излучаемых атомом при радиационном распаде его возбужденного состояния, составляет 100 кГц. Согласно принципу неопределенности время жизни атома в этом состоянии… | |||
| Варианты ответов: | |||
| 1) |  с с
| 2) |  с с
|
| 3) |  с с
| 4) |  с с
|
| Задание 3.14 | |||
Время излучения фотона атомом  с. Интервал частот, которые излучает атом, равен… с. Интервал частот, которые излучает атом, равен…
| |||
| Варианты ответов: | |||
| 1) |  Гц Гц
| 2) |  Гц Гц
|
| 3) |  Гц Гц
| 4) |  Гц Гц
|
| Задание 3.15 | |||
| Стационарным уравнением Шредингера для частицы в трехмерной потенциальной «яме» с бесконечно высокими стенками является... | |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 3.16 | |||
Волновая функция частицы в потенциальной «яме» с бесконечно высокими стенками шириной  имеет вид имеет вид  . Величина импульса этой частицы в основном состоянии равна: . Величина импульса этой частицы в основном состоянии равна:
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 3.17 | |||
| Установите соответствие уравнений Шредингера их физическому смыслу: | |||
| 1)нестационарное 2)стационарное для микрочастицы в потенциальной одномерной «яме» 3)стационарное для электрона в атоме водорода и водородоподобном ионе 4)стационарное для гармонического осциллятора | А)  Б)
Б)  В)
В)  Г)
Г)  Д)
Д) 
| ||
| Варианты ответов: | |||
| 1) | 1-Г, 2-В, 3-А, 4-Б | 2) | 1-А, 2-Б, 3-Г, 4-В |
| 3) | 1-В, 2-Б, 3-А, 4-Д | 4) | 1-Г, 2-Б, 3-А, 4-В |
| Задание 3.18 | |||
Волновая функция частицы в потенциальной «яме» с бесконечно высокими стенками шириной  имеет вид имеет вид  . Если величина импульса этой частицы равна . Если величина импульса этой частицы равна  , то длина волны де Бройля равна… , то длина волны де Бройля равна…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 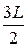
| 4) | 
|
| Задание 3.19 | ||||
Вероятность обнаружить частицу на участке  одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле  , где , где 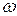 – плотность вероятности, определяемая – плотность вероятности, определяемая  -функцией. Если -функцией. Если  -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке  равна… равна…
| 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.20 | ||||
Вероятность обнаружить частицу на участке  одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле  , где , где 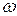 – плотность вероятности, определяемая – плотность вероятности, определяемая  -функцией. Если -функцией. Если  -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке  равна… равна…
| 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.21 | ||||
Вероятность обнаружить частицу на участке  одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле  , где , где 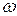 – плотность вероятности, определяемая – плотность вероятности, определяемая  -функцией. Если -функцией. Если  -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке -функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке  равна… равна…
| 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.22 | ||||
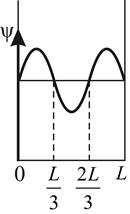
Вероятность обнаружить частицу на участке  одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле одномерной потенциальной «ямы» с бесконечно высокими стенками вычисляется по формуле  , где , где 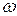 – плотность вероятности, определяемая – плотность вероятности, определяемая  - функцией. Если - функцией. Если  - функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке - функция имеет вид, указанный на рисунке, то вероятность обнаружить частицу на участке  равна… равна…
| 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.23 | |||
На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной «яме» с бесконечно высокими стенками. Состоянию с квантовым числом  соответствует распределение… соответствует распределение…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 3.24 | |||
Электрон в атоме водорода перешел из основного состояния в возбужденное состояние с  . Радиус его боровской орбиты… . Радиус его боровской орбиты…
| |||
| Варианты ответов: | |||
| 1) | не изменился | 2) | увеличился в 2 раза |
| 3) | увеличился в 9 раз | 4) | уменьшился в 3 раза |
| 5) | увеличился в 3 раза |
| Задание 3.25 | ||||
| На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электрона с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Наибольшей частоте кванта в серии Лаймана соответствует переход… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.26 | ||||
| На рисунке изображены стационарные орбиты атома водорода согласно модели Бора, а также условно изображены переходы электрона с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Наибольшей частоте кванта в серии Пашена соответствует переход… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.27 | |||
| Видимую часть спектра излучения атома водорода описывает формула… | |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| Задание 3.28 | |||
В атоме водорода главному квантовому числу  (без учета спина) соответствует… (без учета спина) соответствует…
| |||
| Варианты ответов: | |||
| 1) |  различных квантовых состояний различных квантовых состояний
| 2) |  различных квантовых состояний различных квантовых состояний
|
| 3) |  различных квантовых состояний различных квантовых состояний
| 4) |  различных квантовых состояний различных квантовых состояний
|
| 5) | 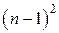 различных квантовых состояний различных квантовых состояний
|
| Задание 3.29 | |||
| В атоме К и L электронные оболочки заполнены полностью. Общее число р-электронов равно… | |||
| Варианты ответов: | |||
| 1) | 2) | ||
| 3) | 4) | ||
| 5) |
| Задание 3.30 | |||
| В атоме К, L и М электронные оболочки заполнены полностью. Общее число электронов равно… | |||
| Варианты ответов: | |||
| 1) | 2) | ||
| 3) | 4) | ||
| 5) |
| Задание 3.31 | ||||
| Установить соответствие квантовых чисел их физическому смыслу | ||||
1)  2)
2)  3)
3) 
| А) определяет ориентации электронного облака в пространстве Б) определяет форму электронного облака В)определяет размеры электронного облака Г)собственный механический момент | |||
| Варианты ответов: | ||||
| 1) | 1-В, 2-Б, 3-А | 2) | 1-В, 2-А, 3-Г | |
| 3) | 1-Г, 2-Б, 3-А | 4) | 1-А, 2-Б, 3-В | |
| Задание 3.32 | |||
Орбитальное квантовое число  определяет… определяет…
| |||
| Варианты ответов: | |||
| 1) | энергию стационарного состояния электрона в атоме | 2) | проекцию орбитального момента импульса электрона на заданное направление |
| 3) | орбитальный механический момент электрона в атоме | 4) | собственный механический момент электрона в атоме |
| Задание 3.33 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… |

| |||
| Варианты ответов: | ||||
| 1) | 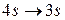
| 2) | 
| |
| 3) | 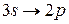
| 4) | 
| |
| Задание 3.34 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… |

| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.35 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.36 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.37 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 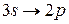
| |
| Задание 3.38 | ||||
| При переходах электрона в атоме с одного уровня на другой закон сохранения момента импульса накладывает определенные ограничения (правило отбора). Если система энергетических уровней атома водорода имеет вид, представленный на рисунке, то запрещенными переходами являются… | 
| |||
| Варианты ответов: | ||||
| 1) | 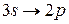
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.39 | ||||
| На рисунке схематически представлена система энергетических уровней атома водорода. Правилами отбора запрещены переходы… | 
| |||
| Варианты ответов: | ||||
| 1) | 
| 2) | 
| |
| 3) | 
| 4) | 
| |
| Задание 3.40 | |||
Задана пси-функция  частицы. Вероятность того, что частица будет обнаружена в объеме частицы. Вероятность того, что частица будет обнаружена в объеме  , определяется выражением… , определяется выражением…
| |||
| Варианты ответов: | |||
| 1) | 
| 2) | 
|
| 3) | 
| 4) | 
|
| 5) | 
|