В этой статье речь пойдет о фигурах на квадратной решетке. В этом разделе присутствует несколько типов задач, это:
1) определение градусной меры угла;
2) определение тангенса угла (косинуса, синуса);
3) определение площади той или иной фигуры – трапеции, параллелограмма, сектора круга, треугольника и т.п.;
4) определение наибольшей (наименьшей) медианы (высоты) треугольника;
5) определение радиуса вписанной в треугольник (описанной около треугольника) окружности;
6) определение площади сложных или составных фигур.
Разберем задачи каждого типа.
Определение градусной меры угла.
1. Определите градусную меру угла:
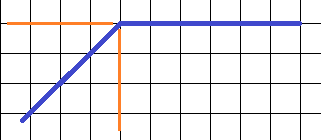
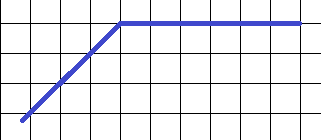
Данный угол – тупой, и можно заметить, что левый луч, образующий его, является биссектрисой прямого угла (см. второй рисунок, угол показан рыжими прямыми). Тогда градусная мера этого угла равна: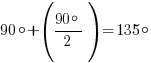 
Ответ: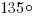 
2. Определите градусную меру угла (имеется в виду “рыжий” угол):
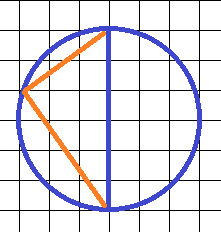
В этой задаче все просто, если вспомнить, что любой угол, вписанный в окружность и опирающийся на диаметр, равен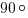 
Ответ: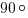
3. Определите градусную меру угла (рыжий).
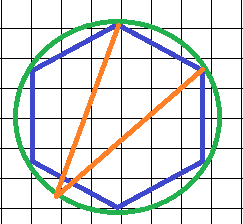
Имеем правильный шестиугольник. Угол, градусную меру которого нам надо определить – вписанный.
Он опирается на дугу, которую стягивает хорда, являющаяся стороной шестиугольника. Тогда центральный угол, опирающийся на ту же дугу, это 1/6 часть всей окружности, или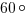 
. Вписанный угол вдвое меньше центрального, если они опираются на одну и ту же дугу, значит, искомый угол равен 
.
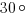4. Определите градусную меру угла.
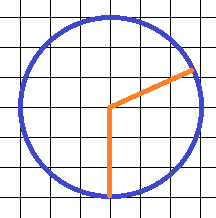
“Нехорошая” задача. В данной задаче определить градусную меру угла можно только приближенно, однако мы не можем вписать приближенный ответ в бланк. Выделенный рыжим угол – тупой, можно заметить, что он состоит из прямого угла и еще некоторой части. Эту часть можно определить только “на глаз” – прикинуть, что она составляет примерно третью часть прямого угла, или 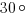. Тогда весь угол – 
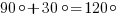. Ответ – 
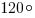. К сожалению такие задачи, где приходится прикидывать, встречаются.
Определение синусов, косинусов, тангенсов углов.
Здесь придется вспомнить геометрические определения синуса, косинуса, тангенса:
Синус угла – отношение противолежащего катета к гипотенузе.
Косинус угла – отношение прилежащего катета к гипотенузе.
Тангенс угла – отношение противолежащего катета к прилежащему.
5. Определить синус, косинус и тангенс угла.
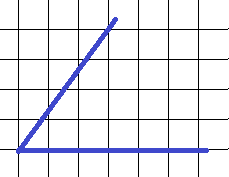
Для того, чтобы воспользоваться определениями синуса, косинуса и тангенса, надо сначала выделить прямоугольный треугольник.
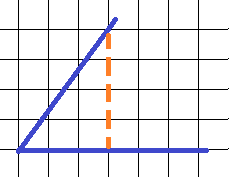
Конечно, удобнее вычислять, если катеты и гипотенуза этого треугольника будут целыми числами. Катеты, понятно, лежат на прямых, образующих саму решетку, поэтому нужно смотреть на луч этого угла, который станет гипотенузой нашего треугольника, и найти такое место, где этот луч пересечет узел решетки:
Тогда в нашем треугольнике катеты – 3 и 4 клетки, а гипотенузу найдем по теореме Пифагора.
Тогда: синус угла – 4/5, или 0,8, косинус угла – 3/5, или 0,6, тангенс угла – 4/3, или 1,33 – кстати, вы подумали, как записать такое число в бланк ответов?
6. Определить тангенс угла:
Вспомним, что тангенс тупого угла равен тангенсу острого, смежного с ним, взятого с отрицательным знаком.
Надо найти тангенс смежного острого угла. Так как луч, образующий его – гипотенуза прямого угла и проходит прямо по узлам решетки, то катеты треугольников, образуемых этим лучом, всегда равны. Тогда тангенс равен: 
. Искомый тангенс тупого угла – (-1).
Ответ: -1
7. Определить тангенс угла.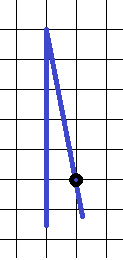 
Данный угол – острый, его тангенс – положительный. Осталось найти подходящий узел решетки, чтобы построить прямоугольный треугольник (для этого черным помечена опорная точка – узел решетки). В этом треугольнике считаем количество клеточек в каждом из катетов и определяем тангенс. У нас катеты – 1 и 4 клеточки, искомый тангенс –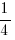 
.
8. Определить тангенс угла.
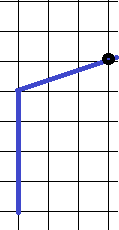
Данный угол – тупой, значит, его тангенс – отрицателен. Определяем тангенс смежного с ним острого угла, ставим перед ним минус – и дело в шляпе. Чтобы определить тангенс острого угла, выбираем целый узел, через который проходит луч, образующий угол – помечен черной точкой. Катеты получившегося треугольника – 1 и 3 клетки, тангенс равен отношению противолежащего катета к прилежащему, значит,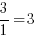 
. Искомый тангенс тупого угла – (-3).
Ответ: -3
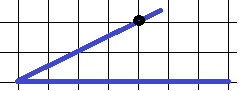
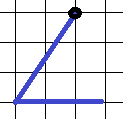
9 и 10. Попробуйте сами определить тангенсы углов на рисунках ниже. Ответ – в конце статьи.
Определение площади той или иной фигуры.
11. Определите площадь трапеции:
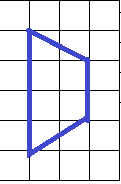Несмотря на то, что трапецию уложили на бок, сразу можем определить, где у нее основания – ведь, чтобы определить площадь трапеции, нужно знать основания и высоту трапеции:
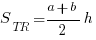
У нас верхнее (малое) основание – 2 клетки, нижнее (большое) – 4 клетки. Высота трапеции – 2 клетки. Тогда вычисляем площадь: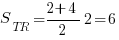 
Ответ: 6
12. Определите площадь параллелограмма:
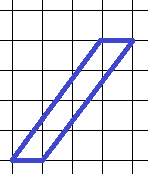
Для вычисления площади параллелограмма достаточно высоты и основания (есть, конечно, и другие формулы, но в данном случае, на решетке, они вряд ли пригодятся):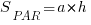 
. У данного параллелограмма основание равно 1 клетке, а вот высота? Высота – всегда перпендикуляр к основанию… или к его продолжению! Вы согласны, что высота этого параллелограмма равна 4 клеткам? Тогда его площадь 
.
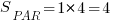Ответ:4.
13. Определите площадь ромба.
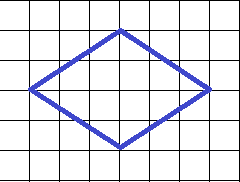Нетрудно понять, что посчитать площадь ромба удобно, разделив его на треугольники либо по вертикали, либо по горизонтали. Имеем два треугольника с основанием 6 клеток, высотой 2 клетки (поделила по горизонтали). Площадь треугольника определяем по формуле: 
.
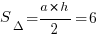Площадь ромба равна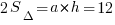 
.
Кстати, площадь ромба здесь еще очень удобно определить как половину произведения его диагоналей: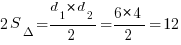 
.
14. Определите площадь кругового сектора, в ответ запишите площадь, деленную на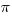 
.
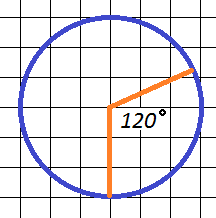
Радиус окружности равен 3, поэтому площадь всего круга будет: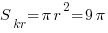 
.
Так как центральный угол сектора равен 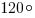, а это 1/3 от 
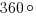, то площадь сектора будет равна 1/3 от площади всего круга, то есть 
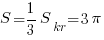. Делим на число 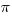и записываем ответ: 3
15. Определите площадь треугольника:
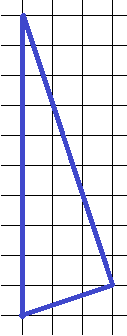
Чтобы найти площадь треугольника, нужно знать его основание и высоту. За основание может быть принята любая удобная сторона, удобная – значит, она расположена строго вертикально или горизонтально – так, чтобы ее длину в клеточках было удобно считать. Здесь возьмем за основание самую длинную сторону, расположенную вертикально, ее длина в клеточках – 10. Проведем к этой стороне высоту из правой вершины, высота получится равной 3 клеточкам. Тогда площадь этого треугольника: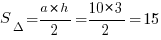 
.
Ответ:15.
16. Определите площадь треугольника:
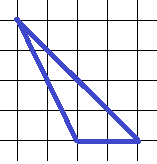
Основание его равно 2 клеткам, высота – 4 клеточки, и неважно, что она не “попала” в основание, ведь она может быть опущена и на его продолжение. Тогда площадь равна: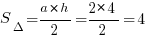 
.
Ответ: 4.
Определение наибольшей или наименьшей высоты (или медианы) треугольника.
17. Определите наименьшую высоту треугольника. Размер клетки 1 см. Ответ дайте в см.
Проведем высоты из вершин данного треугольника к основаниям или их продолжениям:
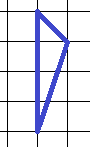
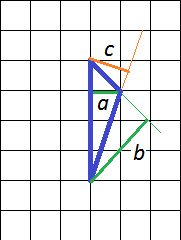
Понятно, что самая маленькая высота – та, что внутри треугольника (а). Ее длина – 1 клеточка.
Ответ: 1
18. Найдите наибольшую медиану треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.
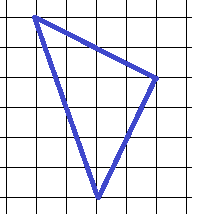
В этом треугольнике нетрудно определить середины сторон – точки, в которых медианы пересекутся со сторонами треугольника (отмечены черными кружочками). Но медианы получаются близкими по длине – как узнать, какая все же длиннее?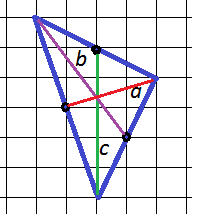 
Очевидно, что борьба развернется между медианами “b” и “c”, “а” – не конкурент, она явно короче. Длину “с” можно определить сразу – это 5 клеточек. Осталось разобраться с медианой “b”, и здесь нельзя выполнить расчет неточно. Воспользуемся тем, что треугольник изображен на сетке – тогда можно использовать теорему Пифагора. Построим прямоугольный треугольник на гипотенузе “b”:
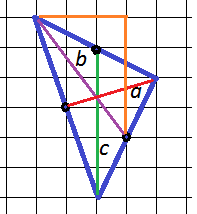
Видно, что катеты этого треугольника 3 и 4 клетки, тогда гипотенуза (это и есть наша медиана “b”) равна 5 и равна медиане “с”. В ответ нужно записать длину наибольшей медианы, ответ: 5
19. Найдите наименьшую медиану треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.
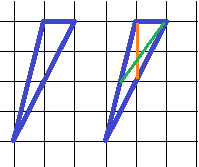
Проведем медианы. Самую длинную медиану (к самой короткой стороне треугольника) не проводим.
Какая из медиан короче – рыжая или зеленая? Если заметить, что два этих отрезка являются перпендикуляром и наклонной между двумя параллельными прямыми, образующими саму сетку, то очевидно, что перпендикуляр – рыжая медиана – короче (по теореме). Ее длина – 2 клетки, записываем ответ: 2.
20. Найдите наибольшую высоту треугольника, изображенного на клетчатой бумаге с размером клетки 1 см. Ответ дайте в см.
Очевидно, что здесь наибольшая высота – это высота, проведенная к продолжению наименьшей стороны треугольника, ее длина составит 4 клетки. Ответ: 4.
Определение радиуса вписанной в треугольник (описанной около треугольника) окружности.
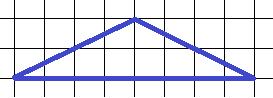
21. Для данного треугольника определите радиус описанной около него окружности. Размер клетки – 1 см. Ответ дайте в см.
В такого типа задачах может помочь знание формул. Нужно помнить, что
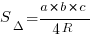, где a, b и c – стороны треугольника, R – радиус описанной окружности.
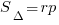, где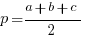 
– полупериметр треугольника, r – радиус вписанной окружности.
Площадь этого треугольника –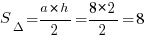 
. Длины его сторон: основание – 8, боковые – по теореме Пифагора –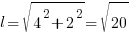 
Считаем радиус описанной окружности: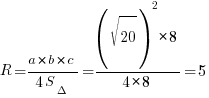 
Ответ: 5
22. Определить радиус вписанной в треугольник окружности. Размер клетки 1 см.
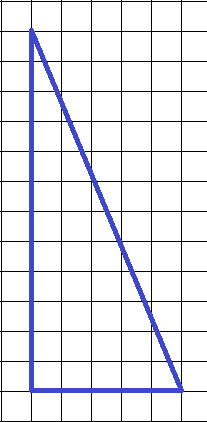
Снова понадобятся стороны – чтобы определить полупериметр. Катеты: 5 и 12, тогда гипотенуза – 13 (пифагорова тройка).
Полупериметр: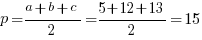 
Это прямоугольный треугольник, площадь найдем через катеты: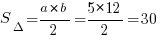 
Тогда радиус вписанной окружности: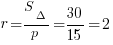 
Ответ:2
23. Определим радиус описанной около треугольника окружности:
Самая длинная – 10, самая короткая –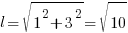 
.Его площадь мы нашли в задаче 15, она равна 15 квадратным см. Осталось найти стороны.
Средняя: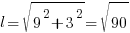 
.
Считаем радиус описанной окружности: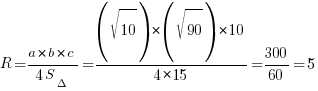 
Ответ:5
Определение площади сложных или составных фигур.
При определении площадей сложных фигур часто их можно разбить на более простые, определить их площади и затем сложить. Но в ряде случаев можно пользоваться и формулой Пика. Она подходит для фигур, нарисованных на клетчатой бумаге, и невырожденых -площадь фигуры ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга.
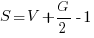
Здесь V – число целочисленных точек внутри фигуры (целочисленные точки – это узлы нашей решетки), G – число целочисленных точек на границе фигуры (на линиях, ограничивающих фигуру). Применять формулу для фигур, содержащих элементы круга не стоит – речь идет о фигурах, полученных при пересечении прямых.
Однако сначала разберем простые случаи.
24. Определите площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.
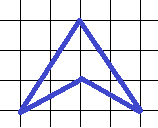
Видно, что фигура состоит из двух треугольников, причем площадь маленького нужно вычесть из площади большого. Определяем площади, большой треугольник: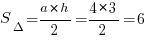 
. Малый треугольник: 
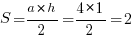. Вычитаем из большей площади меньшую: 4. Ответ: 4.
Попробуем воспользоваться формулой Пика: 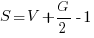. Внутри фигуры три узла решетки, на границе – 4. Тогда площадь: 
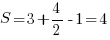– как видите, ответ тот же.
25. Определите площадь квадрата, размер клетки 1 см. Ответ дайте в кв. см.
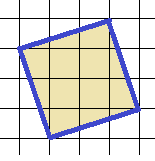
Очень хочется повернуть квадрат так, чтобы стоял на стороне, и сказать, что сторона равна 3, а площадь – 9. Но это не так. Определим длину стороны квадрата по теореме Пифагора: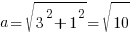 
. Тогда площадь этого квадрата равна 10. Ответ: 10.
Получится ли такой же ответ по нашей волшебной формуле? Внутри фигуры девять узлов решетки, на границе – 4 (вершины квадрата). Тогда площадь: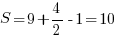 
.
26. Определите площадь заштрихованной фигуры, размер клетки 1 см. Ответ дайте в кв. см.
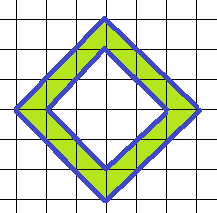
При отыскании площади такой фигуры принцип тот же: находим площадь большого квадрата и вычитаем площадь малого.
Сторона большого квадрата: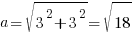 
, значит, его площадь – 18 кв. см.
Сторона малого: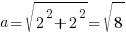 
, его площадь 8 кв. см.
Разность площадей составляет 10 кв. см – это и есть искомая площадь.
По формуле Пика площадь этой фигуры определить нельзя: верный ответ не получится, так как, строго говоря, здесь не одна фигура, а две.
27. Определите площадь кольца. Размер клетки 1 см. В ответ запишите площадь в кв. см, деленную на .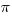
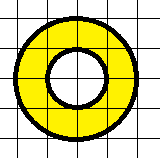
Здесь легко по клеткам определить радиус как большего, так и меньшего круга, посчитать их площади и затем вычесть одно из другого.
Больший круг: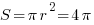 
Меньший круг: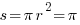 
Разность составляет: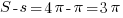 
. В ответ записываем найденную площадь, деленную на число 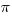: 3
28. Определить площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.
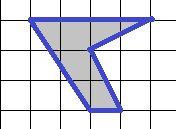
Эту фигуру можно разбить на три треугольника и определить сумму их площадей: 3+1+1=5.
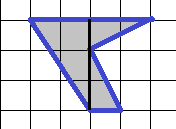
По формуле Пика имеем то же самое: 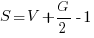. Внутри фигуры два узла решетки, на границе – 8. Тогда площадь: 
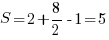– ответ тот же.
29. Определить площадь изображенной на клетчатой бумаге фигуры. Размер клетки 1 см. Ответ дайте в кв. см.
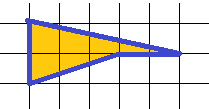
В этом случае надо еще придумать, как разбить нашу фигуру на более простые. Нужно сделать это так, чтобы площади определялись точно, без “ну, там примерно полклеточки”. И это не обязательно должны быть треугольники!
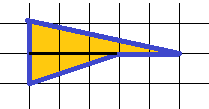
Это могут быть трапеция и треугольник, а площадь трапеции мы уже научились находить. Но в этом случае точно определить площадь можно только разбив фигуру на треугольники: у меня вышло 4 кв. см.
По формуле Пика: внутри два узла решетки, на границе – 6. Тогда площадь: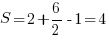 
. Ответ: 4
30. Самостоятельно определите площадь фигуры удобным вам способом:
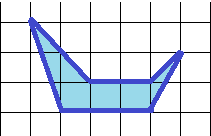Ответ – в конце статьи.
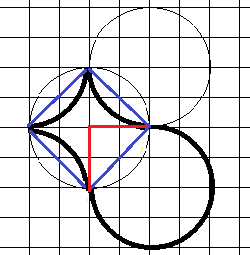
31. Вот такая интересная фигура встретилась на пробном ЕГЭ в 2014 году одному из учеников:
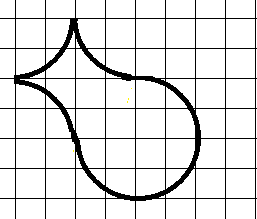
Как тут быть? Можно вычленить полный круг и определить его площадь, но остается еще “рыбий хвост” – этакий сдавленный ромб, и как определить его площадь?
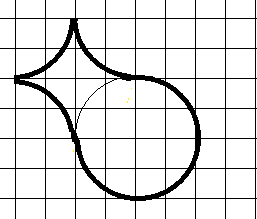
Этот “хвост” – круг, из которого вырезали 8 сегментов – см. рисунок, а площадь сегмента – это площадь сектора (в нашем случае – четверть круга) минус площадь треугольника (красными линиями). Считаем: “тело” рыбы – полный круг. Радиус его 2 клетки, площадь тогда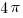 
. Площадь сектора – 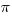, площадь треугольника – 2. Площадь сегмента равна: 
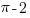, а восьми сегментов – 
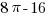. Площадь “хвоста”:
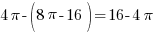. Соединим “хвост” и “тело”: 
.
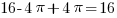Ответ: 16
Ответ на 9 задачу: 1,5
Ответ на 10 задачу: 1/2
Ответ на 30 задачу: 5