Теорема сложения вероятностей

Непосредственный подсчёт случаев, благоприятствующих данному событию, может оказаться затруднительным. Поэтому для определения вероятности события бывает выгодно представить данное событие в виде комбинации некоторых других, более простых событий. Приведём теоремы, с помощью которых можно по вероятностям одних случайных событий вычислять вероятности других случайных событий, каким – либо образом связанных с первыми. Начнём с теорем, которые образуют группу с общим названием «теоремы сложения».

Теорема 1. Пусть А и В – два несовместных события. Тогда вероятность того, что осуществится хотя бы одно из этих двух событий, равна сумме их вероятностей: P(A U B)=P(A)+P(B).

Доказательство.

Обозначим исходы, благоприятные для события А, через а1,а2,…,аm, а для события В – через b1,b2,…,bn. Вероятности этих исходов обозначим соответственно через p1,p2,…,pm и q1,q2,…,qn. Тогда событию A U B благоприятны все исходы a1,a2,…,am, b1,b2,…,bn. В силу того что события А и В несовместны, среди этих исходов нет повторяющихся. Поэтому вероятность события АUB равна сумме вероятностей этих исходов. т.е.

P(AUB)=p1+p2+…+pm+q1+q2+…+qn.

Но p1+p2+pm=P(A), q1+q2+qn=P(B), а потому

P(AUB)=P(A)+P(B).

Теорема доказана.

Пример 1. Стрелок стреляет в мишень. Вероятность выбить 10 очков равна 0,3, а вероятность выбить 9 очков равна 0,6. Чему равна вероятность выбить не менее 9 очков?

Решение. Событие А «выбить не менее 9 очков» является объединением событий В - «выбить 10 очков» и С – «выбить 9 очков». При этом события В и С несовместны, так как нельзя одним выстрелом выбить сразу и 9, и 10 очков.

Поэтому по теореме 1 имеем:

P(A)=P(B)+P(C)=0,3+0,6=0.9.

Если события А1, А2, …,Аn попарно несовместны, то событие A1U … UAn-1 несовместно с событием An. В самом деле,

(A1U…UAn-1) I An =(A1An)U…U(An-1  An).

Но при s<n имеем As An =, и потому (A1U…UAn-1)An =. Пользуясь этим замечанием, получаем из теоремы 1 следствие:

Следствие. Если события А1,…, Аn попарно несовместны, то вероятность объединения этих событий равна сумме их вероятностей:

P(A1U…UAn)=P(A1)+…+P(An).

Доказательство. Как было отмечено выше, события A1U … UAn-1 и An несовместны, а потому по теореме 1имеем:

P(A1U…UAn-1UAn)=P(A1U…UAn-1)+P(An).

Применяя это же рассуждение к первому слагаемому и продолжая далее, получаем после n-1 шага, что

P(A1U … UAn)=P(A1)+…+P(An).

Пример 2. В цехе работает несколько станков. Вероятность того, что за смену потребует наладки ровно один станок, равна 0,2. Вероятность того, что за смену потребуют наладки ровно два станка, равна 0,13. Вероятность того, что за смену потребуют наладки больше двух станков, равна 0,07. Какова вероятность того, что за смену придётся проводить наладку станков?

Решение. В том примере опыт состоит в том, что прошла смена и отмечено, сколько станков за эту смену потребовало наладки. В этом опыте события: А – «за смену потребовал наладки ровно один станок», В – «за смену потребовали наладки ровно два станка» и С – «за сену потребовали наладки более двух станков» несовместны. Нас же интересует вероятность события AUBUC. По теореме 1: P(AUBUC)=P(A)+P(B)+P(C)=0,2+0,13+0,07=0,4.

Выведем теперь связь между вероятностями противоположных событий.

Теорема 2. Для любого события А имеем: P(A*)=1-P(A).

Для доказательства вспомним, что AUA*=U, P(U)=1 и A A*. Тогда по теореме 1 получаем: 1=P(U)=P(AUA*)=P(A)+P(A*), откуда следует требуемая формула.

Пример 3. Берётся наудачу трёхзначное натуральное число от 100 до 999. Какова вероятность того, что хотя бы две его цифры совпадают?

Решение. Опыт здесь состоит в том, что наудачу выбирается натуральное число от 100 до 999 и смотрят, есть ли у негосовпадающие цифры. События «взяли наудачу число N» (N= 100, 101, …, 999) равновероятны (в этом смысл слова «наудачу») и образуют множество исходов этого опыта. Число исходов n=900. Нас интересует событие А - «у выбранного числа совпадают хотя бы две цифры». Проще, однако, подсчитать вероятность противоположного события А* - «у выбранного числа все цифры различны». Каждое такое число есть размещение без повторений из 10 цифр по 3, не имеющее первым элементом нуль. Следовательно, m=(A10)3 –(A9)2=10.9.8—9.8=92.8 (из числа всех трёхэлементных размещений без повторений надо вычесть число тех, у которых на первом месте стоит нуль) и P(A*)=92.8/900=0,72. Тогда по

теореме 2 P(A)=1-P(A*)=0,28.

Пример 4. В урне, содержащей n шаров белого, красного и чёрного цвета, находится k белых шаров и L красных. Какова вероятность вынуть шар не чёрного цвета?

Решение. Если событие А состоит в появлении белого, а событие В – красного шара, то появление шара не чёрного цвета означает появление либо белого, либо красного шара. Так как по определению вероятности

P(A)=k/n, P(B)=L/n,

То по теореме сложения вероятность появления шара не чёрного цвета равна: P(A U B)=k/(n+L)/n=(k+L)/n.

Эту задачу можно решить и так. Пусть событие С состоит в появлении чёрного шара. Число чёрных шаров равно n –(k+L), так что P(C)=(n—k—L)/n. 3

Появление шара не чёрного цвета является противоположным событием С*, поэтому на основании указанного выше следствия из теоремы сложения имеем: P(C*)=1—P(C)=1—(n—k—L)/n=(k+L)/n, как и раньше.

Пример 5. В денежно – вещевой лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность какого – либо выигрыша на один лотерейный билет?

Решение. Если обозначить через А событие, состоящее в выпадении денежного выигрыша, и через В — вещевого, то из определения вероятности следует P(A)=120/1000=0,12; P(B)=80/1000=0,08. Интересующее нас событие представляет (AUB), поэтому из теоремы сложения вытекает:

P(AUB)=P(A)+P(B)=0,20.

Таким образом, вероятность какого – либо выигрыша равна 0,2.

3. Закон равномерной плотности вероятности.

В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.

Дадим определение: равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения:

площадь под кривой распределения равна 1 и поэтому с(в-а)=1

вероятность попадания случайной величины Х на интервал от (α;β)

α=а, если α<а

β=в, если β>в

основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны

Приведем примеры подобных случайных величин:

Пример 1. Произведено взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1г.; результат взвешивания показывает, что вес тела заключен между k и (k+1/2) граммам. Допущенная при этом ошибка X, очевидно, есть случайная величина, распределенная с равномерной плотностью на участке г.

Пример 2. Вертикально поставленное симметричное колесо (см.Рисунок№1) приводится во вращение и затем останавливается вследствие трения. Рассматривается случайная величина θ –угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса ОА. Очевидно величина θ распределена с равномерной плотностью на участке (0,2 π)

Рисунок 1

Итак, я рассмотрю случайные величины и функции распределения.

4. Случайные величины

Определение. Пусть — произвольное вероятностное пространство.

Случайной величиной называется измеримая функция , отображающая в множество действительных чисел , т.е. функция, для которой прообраз любого борелевского множества есть множество из -алгебры .

Примеры случайных величин. 1) Число выпавшее на грани игральной кости.

2) Размер выпускаемой детали. 3) Расстояние от начала координат до случайно брошенной в квадрат точки .

Множество значений случайной величины будем обозначать , а образ элементарного события — . Множество значений может быть конечным, счетным или несчетным.

Определим -алгебру на множестве . В общем случае -алгебра числового множества может быть образована применением конечного числа операций объединения и пересечения интервалов или полуинтервалов вида (), в которых одно из чисел или может быть равно или .

В частном случае, когда — дискретное (не более чем счетное) множество, -алгебру образуют любые подмножества множества , в том числе и одноточечные.

Таким образом -алгебру множества можно построить из множеств или , или .

Будем называть событием любое подмножество значений случайной величины : 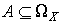. Прообраз этого события обозначим . Ясно, что ; ; . Все множества , которые могут быть получены как подмножества из множества , , применением конечного числа операций объединения и пересечения, образуют систему событий. Определив множество возможных значений случайной величины — и выделив систему событий , построим измеримое пространство . Определим вероятность на подмножествах (событиях) из таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом: .

Тогда тройка назовем вероятностным пространством случайной величины , где

— множество значений случайной величины ; — -алгебра числового множества ; — функция вероятности случайной величины .

Если каждому событию поставлено в соответствие , то говорят, что задано распределение случайной величины . Функция задается на таких событиях (базовых), зная вероятности которых можно вычислить вероятность произвольного события . Тогда событиями могут быть события .

5. Функция распределения и ее свойства

Рассмотрим вероятностное пространство , образованное случайной величиной .

Определение. Функцией распределения случайной величины называется функция действительного переменного , определяющая вероятность того, что случайная величина примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа :

(1)

Там где понятно, о какой случайной величине , или 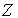идет речь, вместо будем писать . Если рассматривать случайную величину как случайную точку на оси , то функция распределения с геометрической точки зрения это вероятность того, что случайная точка в результате реализации эксперимента попадет левее точки .

Очевидно что функция при любом удовлетворяет неравенству . Функция распределения случайной величины имеет следующие свойства:

2) Функция распределения — неубывающая функция , т.е. для любых и , таких что , имеет место неравенство .

Доказательство. Пусть и и . Событие, состоящее в том, что примет значение, меньшее, чем , представим в виде объединения двух несовместных событий и : .

Тогда согласно аксиоме 3 Колмогорова, или по формуле (1)

, (2)

откуда , так как 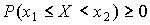. Свойство доказано.

Теорема. Для любых и вероятность неравенства вычисляется по формуле

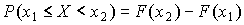(3)

Доказательство. Справедливость формулы (3) следует из соотношения (2). Таким образом, вероятность попадания случайной величины в полуинтервал равна разности значений функции распределения вычисленных на концах полуинтервала и .

2) ; .

Доказательство. Пусть 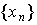и — две монотонные числовые последовательности, причем , при . Событие состоит в том, что . Достоверное событие эквивалентно объединению событий :

; .

Так как , то по свойству вероятностей , т.е. .

Принимая во внимание определение предела, получаем ;

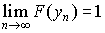
3) Функция непрерывна слева в любой точке ,

Доказательство. Пусть 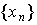— любая возрастающая последовательность чисел, сходящаяся к . Тогда можно записать:

На основании аксиомы 3

Так как ряд справа состоит из положительных чисел и сходится к , то остаток ряда, начиная с некоторого номера 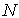, будет меньше , (теорема об остатке ряда)

.

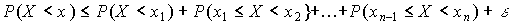Используя формулу (3), выразим вероятности событий через функцию распределения. Получим

,

откуда 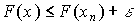или , а это означает, что .

Из рассмотренных свойств следует, что каждая функция распределения является 1) неубывающей, 2) непрерывной слева и 3) удовлетворяет условию и . И, обратно, каждая функция, обладающая свойствами 1), 2), 3), может рассматриваться как функция распределения некоторой случайной величины.

Теорема. Вероятность того, что значение случайной величины больше действительного числа , вычисляется по формуле .

Доказательство. Достоверное событие представим в виде объединения двух несовместных событий и . Тогда по 3-1 аксиоме Колмогорова или 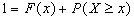, откуда следует искомая формула.

Определение. Будем говорить, что функция распределения имеет при скачок , если , где и пределы слева и справа функции распределения в точке .

Теорема. Для каждого из пространства случайной величины имеет место формула

Доказательство. Приняв в формуле (3) , и перейдя к пределу при , , согласно свойству 3), получим искомый результат. Можно показать, что функция может иметь не более чем счетное число скачков. Действительно функция распределения может иметь не более одного скачка , скачков — не более 3-х, скачков не более чем .Иногда поведение случайной величины характеризуется не заданием ее функции распределения, а каким-либо другим законом распределения, но так, чтобы можно было получить из этого закона распределения функцию распределения .

Список литературы

Для подготовки данной работы были использованы материалы с сайта https://ref.com.ua