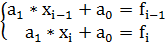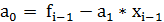ЗАДАЧА ИНТЕРПОЛЯЦИИ
Пусть функция 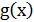 задана таблицей своих значений на интервале [
задана таблицей своих значений на интервале [  :
:
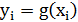 , , 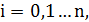 
| (1.1) |
n - количество узлов.
Задача интерполяции - найти функцию 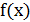 , принимающую в точках
, принимающую в точках 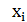 те же значения
те же значения  .
.
При этом предполагается, что среди значений  нет одинаковых. Точки
нет одинаковых. Точки 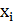 называют узлами интерполяции. Узлы интерполяции не обязательно должны располагаться равномерно на отрезке [
называют узлами интерполяции. Узлы интерполяции не обязательно должны располагаться равномерно на отрезке [  .
.
Функция  называется интерполянтом функции
называется интерполянтом функции 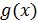 .
.
Если значение  ищется на интервале [
ищется на интервале [  , то эту задачу принято называть задачей интерполяции, а если за пределами этого интервала, то это задачей экстраполяции.
, то эту задачу принято называть задачей интерполяции, а если за пределами этого интервала, то это задачей экстраполяции.
Задача имеет много решений, т.к. через заданные точки, i=0, 1,..., n, можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия (1.2).
В зависимости от цели приближения используют либо интерполяцию (точечную аппроксимацию), либо аппроксимацию. Аппроксимация – это замена таблично заданной функции 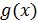 функцией
функцией  , которая на рассматриваемом отрезке имеет ограниченное отклонение от функции
, которая на рассматриваемом отрезке имеет ограниченное отклонение от функции 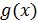 .
.
Условие интерполяции:
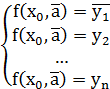
| (1.2) |
Где а – вектор неизвестных коэффициентов.
Обычно вид  известен заранее. Чтобы решить задачу интерполяции необходим коэффициент
известен заранее. Чтобы решить задачу интерполяции необходим коэффициент 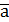 .
.
Решить задачу интерполяции - значит найти при заданных 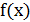 и
и 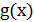 .
.
В общем виде система представляет систему нелинейных уравнений и при больших n часто не имеет решений.
Первым методом решений задачи интерполяции является метод Лагранжа.
Простейшим и наиболее часто применяемым функцией  является полином:
является полином:
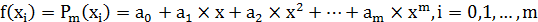
| (1.3) |
где 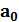 ,
, 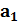 ,
, 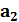 , …,
, …, 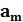 – коэффициент полинома,
– коэффициент полинома,
m – степень аппроксимирующего многочлена.
Интерполирование состоит в приближённой замене функции 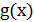 , заданной таблично, функцией
, заданной таблично, функцией 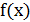 , которая принимает те же значения, что и функция
, которая принимает те же значения, что и функция 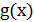 .
.
Все методы интерполяции можно разделить на локальные и глобальные. В случае глобальной интерполяции отыскивается единый полином на всем интервале [  . Методы глобальной интерполяции обычно применяют для функций, заданных небольшим количеством точек, т. к. при увеличении количества точек увеличивается порядок интерполирующего многочлена, что отрицательно сказывается на гладкости получаемой функции. Многочленная аппроксимация, использующая сразу все узлы таблицы (глобальная интерполяция) имеет существенный недостаток – возможность появления больших экстремумов в промежутках между узлами сетки. Т.е. интерполяционный полином может иметь колебания, не свойственные исходным данным. Кроме того, с ростом степени полинома происходит быстрое накопление ошибок округления. Чтобы избежать этих нежелательных эффектов, на практике применяют локальную интерполяцию.. В случае локальной интерполяции на каждом интервале [
. Методы глобальной интерполяции обычно применяют для функций, заданных небольшим количеством точек, т. к. при увеличении количества точек увеличивается порядок интерполирующего многочлена, что отрицательно сказывается на гладкости получаемой функции. Многочленная аппроксимация, использующая сразу все узлы таблицы (глобальная интерполяция) имеет существенный недостаток – возможность появления больших экстремумов в промежутках между узлами сетки. Т.е. интерполяционный полином может иметь колебания, не свойственные исходным данным. Кроме того, с ростом степени полинома происходит быстрое накопление ошибок округления. Чтобы избежать этих нежелательных эффектов, на практике применяют локальную интерполяцию.. В случае локальной интерполяции на каждом интервале [ 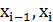 ] строится отдельный полином. Для локальной интерполяции количество узлов большого значения не имеет.
] строится отдельный полином. Для локальной интерполяции количество узлов большого значения не имеет.
Рассмотрим некоторые виды локальной и глобальной интерполяции.
Локальная интерполяция:
1. Кусочно-линейная интерполяция
2. Интерполяция сплайнами
Глобальная интерполяция:
1. Полином Лагранжа
2. Многочлен Ньютона
ГЛОБАЛЬНАЯ ИНТЕРПОЛЯЦИЯ
Интерполяция полиномом Лагранжа
При глобальной интерполяции на всем интервале 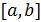 строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:
строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:
Интерполяционный полином Лагранжа n-ой степени есть линейная комбинация базисных полиномов Лагранжа:
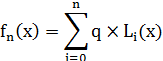
| (2.1) |
где 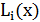 – базисные многочлены степени n:
– базисные многочлены степени n:

| (2.2) |
То есть многочлен Лагранжа:
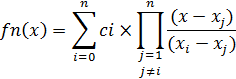
| (2.3) |
Многочлен 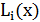 удовлетворяет условию
удовлетворяет условию 
Это условие означает, что многочлен равен нулю при каждом 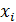 кроме
кроме 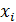 , то есть
, то есть  ,
, 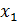 , …
, … 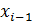 ,
, 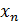 – корни этого многочлена. Таким образом, степень многочлена
– корни этого многочлена. Таким образом, степень многочлена 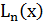 равна n и при
равна n и при 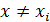 в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером i=j, равного
в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером i=j, равного 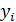 .
.
 принимает значение 1 в точке
принимает значение 1 в точке  и 0 в остальных узлах интерполяции. Следовательно в точке
и 0 в остальных узлах интерполяции. Следовательно в точке  исходный полином принимает значение
исходный полином принимает значение 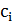
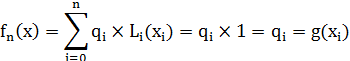
| (2.4) |
Выражение (2.1) применимо как для равноотстоящих, так и для не равноотстоящих узлов.
Многочлен Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисление проводить заново.
2.2. Многочлен Ньютона
Пусть функция g(x) задана с произвольным шагом и точки таблицы значений занумерованы в произвольном порядке.
Многочлен Ньютона во многом опирается на понятие разделенных разностей.
Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:
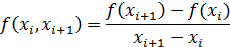
| (2.5) |
Разделенные разности второго порядка определяются через разделенные разности первого порядка:
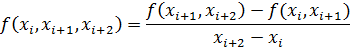
| (2.6) |
Разделенные разности k-го порядка определяются через разделенную разность порядка 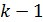 :
:
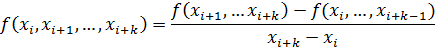
| (2.7) |
Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:
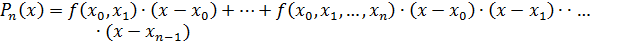
| (2.8) |
Для повышения точности интерполяции в сумму могут быть добавлены новые члены, что требует подключения дополнительных узлов. При этом для формулы Ньютона безразлично, в каком порядке подключаются новые узлы, в то время как для многочлена Лагранжа при добавлении новых узлов все расчеты надо производить заново.
Предположим, что необходимо увеличить степень многочлена на единицу, добавив в таблицу еще один узел  . Для вычисления достаточно добавить к
. Для вычисления достаточно добавить к 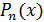 лишь одно слагаемое
лишь одно слагаемое 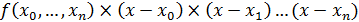
ЛОКАЛЬНАЯ ИНТЕРПОЛЯЦИЯ
3.1. Кусочно-линейная интерполяция.
Одним из самых используемых и простейших видов локальной интерполяции, является кусочно-линейная интерполяция, при которой каждые две точки  и
и 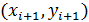 табличной функции
табличной функции  соединяются отрезками прямой (т.е. проводится полином первой степени)
соединяются отрезками прямой (т.е. проводится полином первой степени)
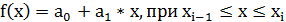
| (3.1) |
А сама функция приближается к ломаной с вершинами в данных точках.
Рисунок 1
Коэффициенты уравнений прямых 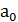 и
и 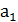 разные на каждом интервале
разные на каждом интервале 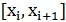 легко находятся из условий интерполяции на концах отрезка:
легко находятся из условий интерполяции на концах отрезка:
| ||||||||||
|
Кусочно-линейная интерполяция является самой простой, и поэтому довольно часто применяется для расчета значений между узлами интерполяции. Для построения интерполирующей зависимости, используемой в дальнейших научных и инженерных расчетах, обычно используются более сложные методы интерполяции.
3.2. Интерполяция сплайнами
Иногда требуется обеспечить непрерывность не только интерполирующей функции, но и нужного количества её производных для этого прибегают к интерполяции сплайнами.
Сплайн – функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с алгебраическим многочленом. Максимальная степень из использованных полиномов называется степенью сплайна.
Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса. На практике наиболее часто используются кубические сплайны  – сплайны третьей степени с непрерывной, по крайней мере, первой производной. При этом величина
– сплайны третьей степени с непрерывной, по крайней мере, первой производной. При этом величина  , называется наклоном сплайна в точке (узле)
, называется наклоном сплайна в точке (узле) 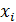 .
.
Разобьём отрезок [a,b] на N равных отрезков [ 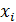 ,
, 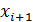 ], где
], где  , i=0,1,…,N-1.
, i=0,1,…,N-1.
Если в узлах 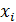 ,
, 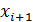 , заданы значения
, заданы значения  ,
,  которые принимает кубический сплайн, то на частичном отрезке [
которые принимает кубический сплайн, то на частичном отрезке [ 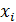 ,
, 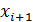 ] он принимает вид:
] он принимает вид:
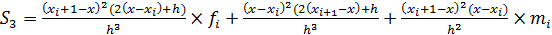 (3.3) (3.3)
|
В самом деле, это легко проверить, рассчитав  и
и  в точках
в точках 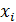 ,
, 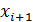
Можно доказать, что если многочлен третьей степени, принимает в точках 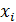 ,
, 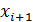 значения
значения  ,
,  и имеет в этих точках производные, соответственно,
и имеет в этих точках производные, соответственно,  ,
, 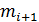 , то он совпадает с многочленом (3.3).
, то он совпадает с многочленом (3.3).
Таким образом, для того, чтобы задать кубический сплайн на отрезке, необходимо задать значения  ,
,  i=0,1…,N в N+1 в узле
i=0,1…,N в N+1 в узле 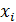 .
.
ОШИБКА ИНТЕРПОЛЯЦИИ
При интерполяции функции всегда получают ошибку состоящую из погрешности самого метода и ошибок округления.
Ошибка приближения функции интерполяционным полиномом n-й степени в точке xопределяется разностью.

| (4.1) |
Можно показать, что погрешность определяется следующим выражением.
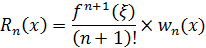
| (4.2) |
Здесь – производная (n+1) порядка функции в некоторой точке, а функция определена как
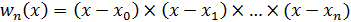
| (4.3) |
Если максимальное значение производной 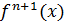 равно,
равно,

| (4.3) |
то для погрешности интерполяции следует оценка.
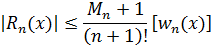
| (4.4) |
Конкретная величина погрешности в точке x зависит, очевидно, от значения функции в этой точке. Качественный характер зависимости показан на рисунке 2.
Из рисунка видно, что погрешность интерполяции тем выше, чем ближе точка x лежит к концам отрезка. За пределами отрезка интерполяции (т.е.
при экстраполяции) быстро растет, поэтому погрешность возрастает существенно.
Рисунок 2
Вследствие описанного поведения погрешности, глобальная интерполяция в некоторых случаях может давать совершенно неудовлетворительный результат.
5. ПРИМЕР ИНТЕРПОЛЯЦИИ ФУНКЦИИ МНОГОЧЛЕНАМИ ЛАГРАНЖА И НЬЮТОНА
Для нахождения многочлена, принимающего в конкретных точках нужные значения, может использоваться пакет Mathcad. В качестве примера рассмотрим задачу на нахождение многочлена Лагранжа удовлетворяющего приведенным исходным данным.
Построим многочлен Лагранжа в пакете Mathcad:
Исходные данные:
ORIGIN:=1
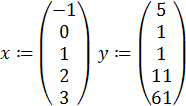
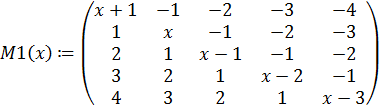
Далее вычисляем лагранжевы коэффициенты 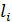 по формуле (2.2):
по формуле (2.2):

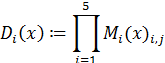
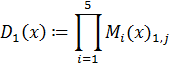

q 
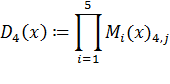

Таким образом лагранжевы коэффициенты:
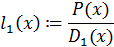
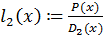

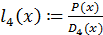
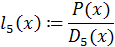
Сам многочлен Лагранжа будет выглядеть так:
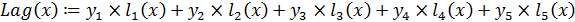
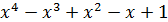
Рисунок 3
Построим многочлен Ньютона по неравностоящей сетке узлов и найдем приближенное значение интерполируемой функции y=f(x) при значении аргумента 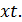
Исходные данные:
ORIGIN:=1



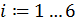
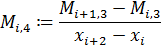
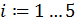
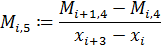
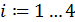
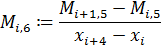
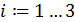
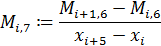
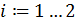
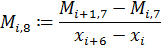
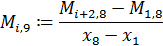
По этим значениям мы получаем таблицу конечных разностей. Набирая числовые значения коэффициентов из нее, по формуле 2.8, мы получаем аналитический вид многочлена.
Значения функции в требуемой точке вычисляется обращением к соответствующей подпрограмме:
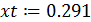
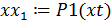
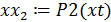



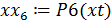
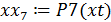
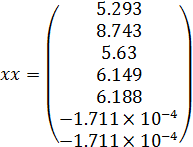
Рисунок 4
6. ЗАКЛЮЧЕНИЕ
Из рассмотренных методов интерполяции – наиболее простой метод интерполяции полиномом Лагранжа, однако у него есть недостатки:
¾ Степень многочлена определяется количеством узлов (минус 1), следовательно, любая попытка повысить точность аппроксимации путем увеличения количества узлов надо производить вычисления заново.
¾ Формула для расчета слишком громоздка.
При интерполяции методом Ньютона, при подключении новых узлов (для повышения точности интерполяции) безразлично в каком порядке их подключать.
7. СПИСОК ЛИТЕРАТУРЫ
1. Вержбицкий, В.М. Основы численных методов / В.М. Вержбицкий. – М.: Высшая школа, 2002. – 840 с. 11
2. Дж. Форсайт, М.Мальком, К. Моулер. Машинные методы математических вычислений. Изд-во "Мир". Москва. 1980
3. В.В. Иванов. Методы вычислений на ЭВМ. Справочное пособие. Изд-во "Наукова думка". Киев. 1986.
4. Бахвалов Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – М.: Бином, 2004. – 634 с.
5. С.Д. Шапорев. Методы вычислительной математики и их приложения: учебное пособие / Балт.гос. техн.ун-т. «Военмех» Спб, 2002. 230 с.
6. Учебное пособие по курсу "Численные методы в оптике"[Электронный ресурс] https://aco.ifmo.ru/el_books/numerical_methods/lectures/glava3.html (Дата обращения 08.02.2016)
7. Лекции по численным методам. [Электронный ресурс] https://nickolay.info/study/methods/03.html#kpi (Дата обращения 11.02.2016)
8. Бедарев И.А., Белоусова О.Н., Федорова Н.Н – Численные методы решения инженерных задач в пакете Mathcad: учебное пособие [Электронный ресурс] https://window.edu.ru/catalog/pdf2txt/299/63299/33428?p (Дата обращения 11.02.2016)
9. Постановка задачи. Кусочно-линейная интерполяция. [Электронный ресурс] https://e-lib.gasu.ru/eposobia/metody/R_3_1.html (Дата обращения 12.02.2016)
10. Ануфриев Игорь Евгеньевич. [Электронный ресурс] Вычисления и приближение данных в MATLAB https://matlab.exponenta.ru/spline/book1/10.php (Дата обращения 12.02.2016)