I. Парная линейная корреляционная зависимость

Лабораторная работа № 5

Корреляционный анализ

Цель работы: научиться оценивать наличие, тесноту и направленность связи между значениями двух независимых случайных величин.

I. Парная линейная корреляционная зависимость

При решении различных геологических задач часто необходимо совместно рассмотреть несколько случайных величин. В одних случаях изучаемые свойства геологических объектов проявляются независимо друг от друга, а в других между ними могут быть выявлены более или менее отчетливые взаимосвязи. Во многих случаях бывает важно проследить за изменением одного признака с изменением другого. Т.к. изменение свойств геологических объектов вызывается действием различных факторов, изучаемые взаимосвязи имеют, как правило, статистический характер и практически всегда отличаются от функциональных. Для их изучения и описания используются двумерные и многомерные статистические модели. Зависимость между признаками может быть линейной и нелинейной. В математической статистике взаимосвязь явлений и их признаков изучают методом корреляции.

Для выявления линейной корреляционной зависимости необходимо иметь хотя бы 2 ряда сопряженных наблюдений случайной величины, признаки определяются в одном объекте (например, образце, пробе и т.д.).

Задание 1. Выявить зависимость между двумя свойствами геологических объектов.

Расчеты требуется произвести "вручную" и проверить с помощью стандартных функций программы Excel. При "ручном" счете заполняется таблица (см. табл.5.1):

Порядок выполнения:

1. Построить точечный график зависимости между свойствами. По графику оценить однородность выборки, линейность зависимости, качественно определить наличие и тесноту связи (тесная, средняя, слабая, отсутствует) и ее характер (прямая, обратная).

Примечание: При выявлении корреляционной зависимости ни в коем случае нельзя упорядочивать или как-либо сдвигать данные.

2. Рассчитать статистические характеристики системы двух случайных величин (среднеарифметические значения, дисперсии, стандартные отклонения, ковариацию, коэффициент корреляции).

Обозначим: x_i – значения одной случайной величины, y_i – значения другой случайной величины.

2.1. Среднеарифметические значения и 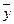рассчитывают по формуле (1.4).

(1.4)

где n – объем выборки^[1]; х _i – i -тое значение выборки.

Таблица 5.1

Расчет коэффициента корреляции

№ п/п	Исходные данные,	Степени отклонений и их произведения
Признак х i	Признак yi
	y 1	х 1	√	√	√	√	√
…	…	…	…	…	…	…	…
n	yn	х n	√	√	√	√	√
∑	√	√	√	√	√	√	√
Сред-нее			μ 1 х = 0	μ 2х S х 2	μ 1 у = 0	μ 2 S у 2	μ 11 Kxy

Примечания: 1) за счет округлений μ _{1 х} и μ _{1 у} могут отличаться от нуля;

2) μ ₁₁ – смешанный центральный момент.

2.2. Дисперсии S_x ², S_y ² и среднеквадратические отклонения S_x и S_y рассчитывают по формулам (1.5 и 1.6)

(1.5)

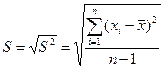(1.6)

2.3. Корреляционный момент, или ковариация, рассчитывается по формуле:

(4.1)

Ковариация измеряется в квадратах единиц измерения случайных величин.

2.4. Коэффициент парной корреляции (r _xy или r):

или (4.2)

Коэффициент корреляции – мера линейной взаимосвязи между двумя случайными величинами. Для характеристики нелинейной зависимости непригоден. Это безразмерная величина, измеряемая либо в долях единицы, либо в процентах. Коэффициент линейной корреляции изменяется в пределах от –1 до +1 и не зависит от точки начала отсчета и единиц измерения.

Если r_xy = 0 – величины некоррелированы, но это не означает, что связи нет, т.к. в этом случае может быть нелинейная зависимость.

Если r_xy стремится к 1 – тесная прямая (положительная) линейная статистическая зависимость. Прямая корреляция характеризует такую статистическую зависимость, когда при возрастании одной случайной величины другая будет в среднем возрастать.

Если r_xy стремится к –1 – тесная обратная (отрицательная) линейная статистическая зависимость (обратная корреляция).

Если |r_xy| = 1 – функциональная линейная зависимость.

3. Проверить полученный коэффициент корреляции с помощью «Мастера функций» программы Excel (функция КОРРЕЛ).

4. Убедиться в том, что коэффициент корреляции значимо отличается от нуля (т.е. проверить надежность корреляции).

Как и при проверке других статистических величин, формулируется отрицательная нулевая гипотеза: Н ₀: r_x,y = 0, (т.е. «коэффициент корреляции статистически не отличается от нуля или, иными словами, значимой линейной корреляции между изучаемыми величинами нет»), при множестве альтернатив Н ₁: r_x,y ≠ 0.

Проверка осуществляется при помощи критерия Стьюдента:

, (4.3)

где r – рассчитанный коэффициент парной линейной корреляции.

Для сравнения используют предельные (табличные) значения двустороннего t -критерия Стьюдента с числом степеней свободы k = n-2 и выбранным уровнем значимости α.

Если | t_эмпир | > t_{(α, k) табл} , связь считается доказанной с доверительной вероятностью p = 1 – α. В противном случае линейная зависимость считается не установленной.

При значительном объеме выборки можно в качестве t_крит брать значения коэффициента вероятности нормального распределения (см. табл.1.3):

Либо можно при выбранном t_крит сразу рассчитать значимое значение коэффициента корреляции по формуле:

, (4.4)

так, например при t_крит =3 (p =0,997) 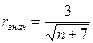и все коэффициенты корреляции будут значимы с p =0,997, если | r | ≥ r_знач.

Формулой (4.4) удобно пользоваться при проверке значимости сразу нескольких коэффициентов корреляции, например, при составлении матрицы коэффициентов корреляции.

5. Обобщить результаты, указать возможные геологические причины выявленных закономерностей.

Задание 2: Рассчитать матрицу коэффициентов корреляции между всеми парами свойств.

Порядок выполнения работы:

1.Рассчитать матрицу коэффициентов корреляции с помощью «Анализа данных» программы Excel: Сервис → Анализ данных → Корреляция. В окне «Входной интервал» ввести адреса ячеек всей таблицы, включая «шапку»; поставить «галочку» в окне «Метки в первой строке»; в строке «Группировать по» задать «по столбцам».

2.Рассчитать величину значимого коэффициента корреляции.