На Рисунке 6.1 представлена схема электропривода постоянного тока после введения СКУ.
В качестве Фазовых координат для метода АКОР выбраны положение вала электропривода его скорость вращения и ток обмотки якоря.
Используя схему на рисунке 6.1 выразим фазовые координаты в систему уравнений в форме Коши(11), где: 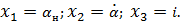

|

|
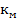
|

|

|

|

|

|
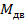
|
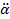
|

|
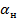
|

|
Рисунок 6.1 схема электропривода после введения СКУ
 (11)
(11)
Запишем систему 11 в форме пространства состояния матрицы А и В под номером 12.
 (12)
(12)
Перепишем систему (11) относительно вектора ошибок:
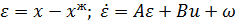 . Полученная система представлена под номером 13.
. Полученная система представлена под номером 13.
 ;
;  (13)
(13)
Закон управления представлен под номером 14.
 (14)
(14)
Матрицы коэффициентов усиления 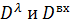 находятся из выражений под номером 15, где:
находятся из выражений под номером 15, где:  .
.
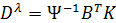 ;
;  (15)
(15)
Для определения матрицы K необходимо решить алгебраическое уравнение Риккати (16).
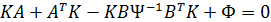 (16)
(16)
Для определения коэффициентов матриц  и
и  можно использовать метод Мэриэма. В основе метода лежит предположение о том, что максимально допустимые отклонения всех фазовых координат в каждый момент времени вносят в функционал (17) одинаковый вклад, а их полный вклад равен суммарному вкладу управляющих сигналов, каждый из которых также вносит одинаковый вклад в указанный функционал. Исходя из этого, можно записать выражения (18).
можно использовать метод Мэриэма. В основе метода лежит предположение о том, что максимально допустимые отклонения всех фазовых координат в каждый момент времени вносят в функционал (17) одинаковый вклад, а их полный вклад равен суммарному вкладу управляющих сигналов, каждый из которых также вносит одинаковый вклад в указанный функционал. Исходя из этого, можно записать выражения (18).
 (17)
(17)
 ;
;
 ; (18)
; (18)
 .
.
Примем  и
и  , а также целесообразно принять матрицы
, а также целесообразно принять матрицы  и
и  диагональными, где:
диагональными, где: 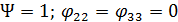 . Тогда функционал (17) примет следующий вид:
. Тогда функционал (17) примет следующий вид:
 (19)
(19)
Исходя из желаемых значений точности и амплитуды управляющего сигнала, а также используя выражения под номером 18, получим значение  .
.
Матрица  имеет вид:
имеет вид:
 . (20)
. (20)
Используя пакет приложений MATLAB решим уравнение Риккати (16), получим матрицу коэффициентов К, подставив её в выражения (15) получим матрицы (21).
 (21)
(21)
Моделирование
На рисунке 7.1 представлена схема оптимального самонастраивающегося привода, собранная в приложении Simulink пакета MATLAB.

Рисунок 7.1 схема оптимального самонастраивающегося привода
На рисунках 7.2 и 7.3 представлены графики реакции ДПТ, замкнутого единичной обратной связью, на первом графике реакция на единичное ступенчатое изменение входного сигнала, на втором графике представлена установившаяся ошибка системы при единичном гармоническом входном сигнале.
Рисунки 7.4, 7.5 и 7.6, 7.7 представляют графики реакции на ступенчатый входной сигнал и установившейся ошибки системы при введении СКУ и ОР.
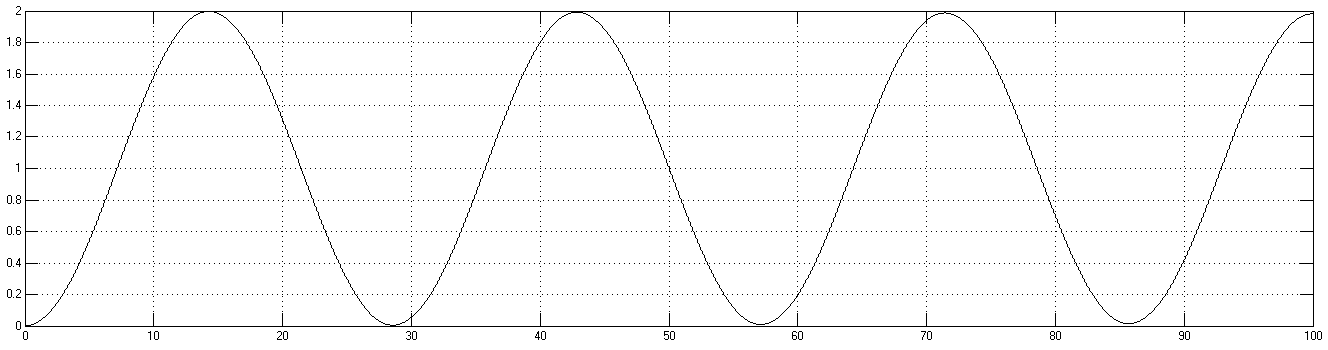
Рисунок 7.2 реакция ДПТ замкнутого еденичной обратной связью на ступенчатый входной сигнал
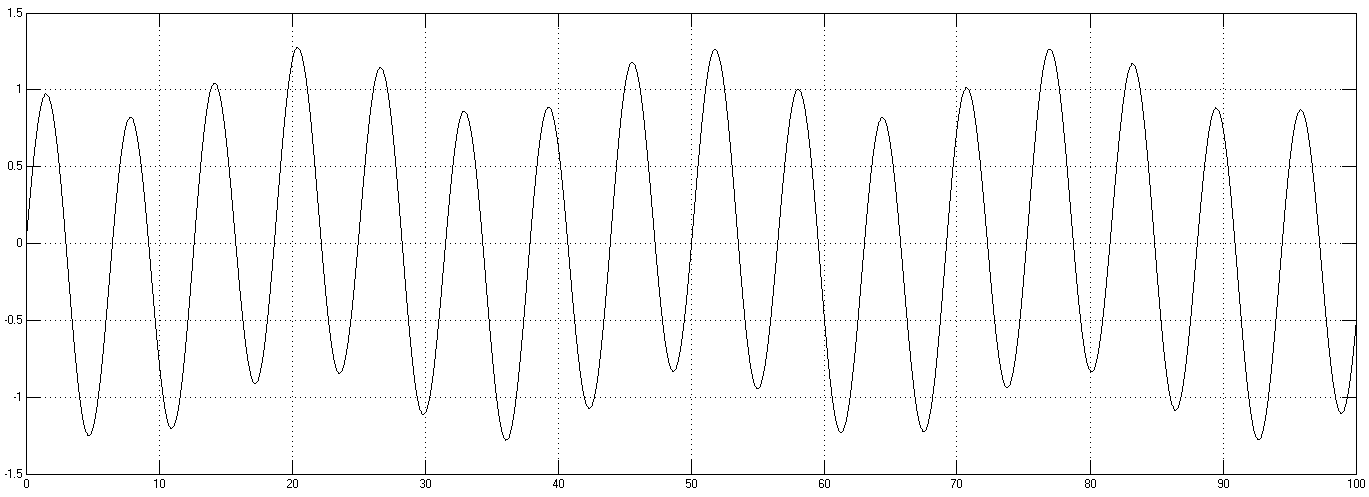
Рисунок 7.3 установившаяся ошибка ДПТ замкнутого еденичной обратной связью при гармоническом входном сигнале
 Рисунок 7.4 реакция ДПТ с СКУ на ступенчатый входной сигнал
Рисунок 7.4 реакция ДПТ с СКУ на ступенчатый входной сигнал

Рисунок 7.5 установившаяся ошибка ДПТ с СКУ при гармоническом входном сигнале
 Рисунок 7.6 реакция ДПТ с СКУ и ОР на ступенчатый входной сигнал
Рисунок 7.6 реакция ДПТ с СКУ и ОР на ступенчатый входной сигнал
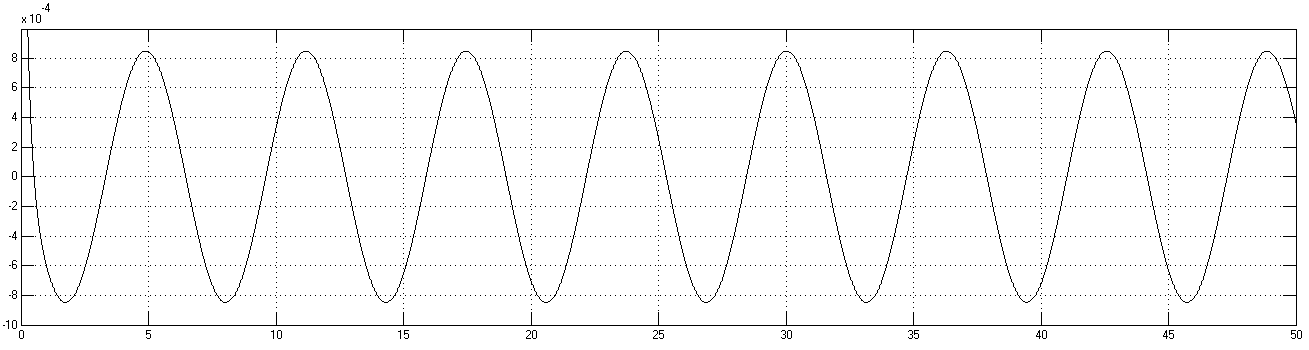 Рисунок 7.7 установившаяся ошибка ДПТ с СКУ и ОР при гармоническом входном сигнале
Рисунок 7.7 установившаяся ошибка ДПТ с СКУ и ОР при гармоническом входном сигнале
Вывод
В ходе выполнения данного курсового проекта была успешно решена ПЗК, результатом её решения стали уравнения кинематики, описывающие положение и ориентацию схвата манипулятора в абсолютной системе координат.
Используя уравнение Лагранжа второго рода (5) были успешно получены обобщённые моменты заданной степени подвижности манипулятора, они были успешно использованы при синтезе СКУ.
Из рисунков 7.2, 7.3 видно, что ДПТ до введения коррекции был неустойчивым, после введения СКУ перерегулирование системы менее 85%, а установившаяся ошибка при гармоническом сигнале не более 0.015(рад).
Для достижения требуемых показателей качества работы системы был синтезирован ОР по квадратичному критерию методом АКОР. Результат работы системы после введения ОР показан на рисунках 7.6 и 7.7, видно, что переходной процесс стал апериодическим, а установившаяся ошибка системы при подаче гармонического сигнала на вход не превышает 0.001(рад).
Полученные показатели качества регулирования, полностью соответствуют поставленным целям.