Объемная плотность энергии может буть найдена по формулам [1]:
и 
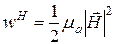
В данном случае, преобразуем эти выражения следющим образом:
, Дж/м3
Запишем выражение для комплексного вектора Пойтинга для двух случаев: когда частота принадлежит найденному в п. 2 диапазону и когда она не принадлежит этому диапазону. Определим среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.
Рассмотрим сначала режим бегущей волны.
Запишем выражения для сопряженных составляющих вектора 
:
Тогда выражение для вектора Пойтинга примет вид:
Упростив это выражение, получаем конечный вариант выражения для вектора Пойтинга:
Заметим, что составляющие по оси х и по оси у чисто мнимые, составляющая по оси z – действительная, значит вдоль z и происходит перенос энергии. Тогда:
Для второго случая сопряженные составляющие вектора примут вид:
В этом случае векто пойтинга чисто мнимый и переноса эенергии не происходит.
Запишем выражения для мгновенных значений плотностей активного и реактивного потоков энергии для двух случаев, указанных в п. 8.
Для первого случая:
Упростив выражение, получим:
Исходя из того, что знак активной составляющей не изменяется, а знак реактивной состаляющей меняется дважды за период [1], выделим в полученном выражении активную и реактивную часть:
Для второго случая:
Упростив выражение, получим
Исходя того же утверждения, что и в первом случае, получим:
Вычислим средний за период поток энергии через поперечное сечение волновода.
Для этого проинтегрируем выражения для плотности активного потока энергии по площади поперечного сечения волновода:
, ВА (11)
11. Определим фазовую скорость Vф и скорость распространения энергии Vэ рассматриваемой волны. Рассчитаем и построим графики зависимостей Vф и Vэ от частоты.
За время 
волна распространяется на расстояние 
, при этом фазы волны в моменты времен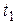и 
и 
в плоскостях 
и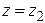 
сответственно совпадают.
здесь 
– фаза в момент времени t=0.
Рассчитаем фазовую скорость волны с учетом 
м.
, м/с
Для расчета скорость распространения энергии Vэ воспользуемся соотношением:
Vэ 
Vэ 
, м/с.
Запишем выражение, характеризующее зависимость фазовой скорости от длины волны в волноводе.
, м/с
Vэ 
, м/с.
Графики зависимостей зависимостей Vф и Vэ от частоты приведены на рис. 14
12. Считая, что стенки трубы выполнены из реального металла имеющего 
Сим/м, на основе граничных условий Леонтовича-Щукина определим коэффициент затухания для заданной волны.
Формула для расчета коэффициента затухания на основе граничных цсловий Леонтовича-Щукина имеет вид [1]:
,
где 
,
Раскроем частотную зависимость коэффициента затухания:
,
Выражение для Рср подставлено из (11).
Подставив 
в полученное выражение для коэффициента затухания, получим:
, Нп/м
Рассчитаем и построим график зависимоти коэффициента затухания волны в волноводе от частоты.
, Нп/м
График этой зависимости представлен на рис. 15
Опеределим тип волны, распространяющейся в волноводе. Изобразим структуру силовых линий электрического и магнитного полей этой волны и плотности поверхностного тока проводимости, протекающего по стенкам волновода.
Данная волна является волной типа 
, так как только вектор имеет продольную составляющую.
Структуры полей волны и поверхностных токов представлены на рис. 16 и 17
рис. 14
рис. 15
рис. 16
рис. 17
Вывод:
В данной работе проведено исследование волны в прямоугольном волноводе. По заданным соотношениям определены все составляющие обоих векторов электромагнитного поля. Проведено исследование зависимости амплитуд составляющих поля от координат в режиме бегущей волны (с переносом энергии) и в режиме стоячей волны (без переноса энергии). В ходе исследования установлено, что вдоль каждой стенки волновода укладывается одна полуволна по осям Х и У соответственно. Показано экспоненциальное затухание волны с ростом координаты z в режиме стоячей волны и неизменность амплитуды ее колебаний с при изменении координаты z в режиме бегущей волны (без учета потерь). Проведена проверка выполнения граничных условий на стенках волнвода. Получены математические выражения для поверхностных токов и зарядов на стенках волновода. Рассчитан вектор Пойтинга в комплексной форме и в форме мгновенного значения. Результаты этого расчета использованы для расчета средней за период энергии, проходящей через поперечное сечение волновода. Рассчитана фазовая скорость и скорость распространения энергии волны в волноводе, их зависимости рассчитана и построена графически. Рассчитан коэффициент затухания волны при использовании волновода из реального металла с заданной проводимостью, его зависиимость от частоты так же рассчитана и показана графически. Установлен тип волны, ее структура, изображенная на соответствующем рисунке.
В процессе выполнения работы противоречий между отдельными е частями не выявлено. Следовательно, математическая модель поля построена верно.
Использованная литература:
[1] - Техническая электродинамика / Пименов Ю.В., Вольман В.И., Муравцов А.Д. Под ред. Ю.В. Пименова: Учебное пособие для вузов. – М.: Радио и связь, 2002.