Существует целый ряд критериев, позволяющих осуществлять выбор стратегии в условиях неопределенности: критерий Вальда, критерий нейтрального игрока, критерий азартного игрока, критерий Сэвиджа, критерий Гурвица и др.
Критерий Вальда (максиминный критерий). Использование этого критерия выбора стратегии считается прерогативой игрока, который, в первую очередь, стремится не выиграть, а не проиграть. Его позицию можно выразить поговоркой: «Лучше синица в руках, чем журавль в небе». Математически этот критерий можно записать следующим образом:

Алгоритм выбора решения: матрица решений дополняется столбцом из наименьших элементов каждой строки. После этого из совокупности этих элементов определяется максимальный.

В соответствии с максиминным критерием наилучшей является стратегия №3, позволяющая получить максимально возможный выигрыш при неблагоприятных условиях.
Критерий нейтрального игрока. Нейтральным считается игрок, который не стремится ни рисковать, ни осторожничать. Его позицию можно выразить фразой: «Золотая середина». Математически этот критерий можно записать следующим образом:

Алгоритм выбора решения: матрица решений дополняется столбцом из среднеарифметических значений элементов для каждой строки. Затем из совокупности этих элементов определяется максимальный.
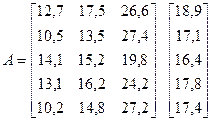
В соответствии с критерием нейтрального игрока наилучшей является стратегия №1, ориентированная на получение усредненной суммы прибыли.
Критерий азартного игрока. Азартным считается игрок, готовый ради максимального выигрыша идти на любой риск. Его позицию можно выразить фразой: «Все или ничего». Математически этот критерий можно записать следующим образом:

Алгоритм выбора решения: матрица решений дополняется столбцом из наибольших элементов каждой строки. Затем из совокупности этих элементов определяется максимальный.

В соответствии с критерием азартного игрока наилучшей является стратегия №2, позволяющая рассчитывать на получение максимально возможного выигрыша.
Критерий Сэвиджа. Данный критерий часто называют критерием минимального риска или критерием минимизации сожалений. Сожаление - это величина, равная изменению полезности решения (результата) при данном текущем состоянии среды относительно наилучшего возможного состояния (для данного решения). Математически этот критерий можно записать следующим образом:

Алгоритм выбора решения: в каждом столбце определяется максимальное значение элементов. Затем матрица исходов преобразуется в матрицу рисков, элементы которой находятся как разница между максимальным элементом для соответствующего столбца и текущим элементом. После этого в каждой строке определяется максимальный элемент, а из совокупности этих элементов определяется минимальный.


В соответствии с критерием Сэвиджа наилучшей является стратегия №1, позволяющая минимизировать величину максимального риска (отклонений от максимально возможных значений для каждого исхода).
Критерий Гурвица. Данный критерий предполагает компромисс между крайним оптимизмом и крайним пессимизмом. Математически этот критерий можно записать следующим образом:
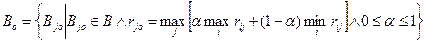
Алгоритм выбора решения: в каждой строке определяются максимальное и минимальное значение элементов. Затем находится сумма произведения весового коэффициента (α) и максимального значения и произведения единицы за минусом весового коэффициента и минимальным значением по каждой строке. Весовой коэффициент α показывает в сторону оптимизма или пессимизма смещается приоритет игрока. При α =0,5 межу оптимизмом и пессимизмом достигается паритет. В данном случае рассмотрим выбор стратегии при α =0,4, то есть при небольшом смещении приоритетов в сторону пессимизма.
Затем из совокупности этих элементов определяется максимальный.


В соответствии с критерием Гурвица наилучшей является стратегия №4, позволяющая найти компромиссный вариант между оптимизмом и пессимизмом со смещением приоритетов в сторону пессимизма.
Задание для самостоятельной работы
Используя условия предлагаемых вариантов, выбрать наилучшие стратегии развития системы по критериям Вальда, нейтрального игрока, азартного игрока, Сэвиджа, Гурвица (α =0,3).
Таблица 33. Исходные данные для решения задачи выбора стратегии
в условиях неопределенности
| № варианта | Стратегии | Условия | № варианта | Стратегии | Условия | ||||
| Неблагоприятные | Средние | Благоприятные | Неблагоприятные | Средние | Благоприятные | ||||
| Стратегия №1 | 12,7 | 15,2 | 18,2 | Стратегия №1 | 14,0 | 18,2 | 20,9 | ||
| Стратегия №2 | 10,5 | 14,8 | 20,5 | Стратегия №2 | 11,6 | 17,8 | 23,6 | ||
| Стратегия №3 | 9,6 | 16,8 | 17,5 | Стратегия №3 | 10,6 | 20,2 | 20,1 | ||
| Стратегия №4 | 13,1 | 16,2 | 18,1 | Стратегия №4 | 14,4 | 19,4 | 20,8 | ||
| Стратегия №5 | 10,2 | 16,8 | 20,0 | Стратегия №5 | 11,2 | 20,2 | 23,0 | ||
| Стратегия №1 | 8,0 | 16,2 | 22,2 | Стратегия №1 | 8,8 | 19,4 | 25,5 | ||
| Стратегия №2 | 14,2 | 14,8 | 15,5 | Стратегия №2 | 15,6 | 17,8 | 17,8 | ||
| Стратегия №3 | 13,8 | 15,5 | 20,3 | Стратегия №3 | 15,2 | 18,6 | 23,3 | ||
| Стратегия №4 | 15,2 | 18,2 | 21,2 | Стратегия №4 | 16,7 | 21,8 | 24,4 | ||
| Стратегия №5 | 10,2 | 12,3 | 20,0 | Стратегия №5 | 11,2 | 14,8 | 23,0 | ||
| Стратегия №1 | 10,4 | 15,7 | 20,2 | Стратегия №1 | 11,4 | 18,8 | 23,2 | ||
| Стратегия №2 | 12,4 | 14,8 | 18,0 | Стратегия №2 | 13,6 | 17,8 | 20,7 | ||
| Стратегия №3 | 11,7 | 16,2 | 18,9 | Стратегия №3 | 12,9 | 19,4 | 21,7 | ||
| Стратегия №4 | 14,2 | 17,2 | 19,7 | Стратегия №4 | 15,6 | 20,6 | 22,6 | ||
| Стратегия №5 | 10,2 | 14,6 | 20,0 | Стратегия №5 | 11,2 | 17,5 | 23,0 | ||
| Стратегия №1 | 9,2 | 16,0 | 21,2 | Стратегия №1 | 10,1 | 19,1 | 24,4 | ||
| Стратегия №2 | 13,3 | 14,8 | 16,8 | Стратегия №2 | 14,6 | 17,8 | 19,3 | ||
| Стратегия №3 | 12,8 | 15,9 | 19,6 | Стратегия №3 | 14,0 | 19,0 | 22,5 | ||
| Стратегия №4 | 16,2 | 17,7 | 20,5 | Стратегия №4 | 16,2 | 21,2 | 23,5 | ||
| Стратегия №5 | 11,2 | 13,5 | 20,0 | Стратегия №5 | 11,2 | 16,1 | 23,0 | ||
| Стратегия №1 | 9,8 | 17,4 | 20,7 | Стратегия №1 | 10,8 | 20,9 | 23,8 | ||
| Стратегия №2 | 12,9 | 16,3 | 17,4 | Стратегия №2 | 14,2 | 19,6 | 20,0 | ||
| Стратегия №3 | 12,3 | 17,7 | 19,3 | Стратегия №3 | 13,5 | 21,2 | 22,2 | ||
| Стратегия №4 | 16,7 | 17,5 | 20,1 | Стратегия №4 | 18,4 | 21,0 | 23,1 | ||
| Стратегия №5 | 11,8 | 14,1 | 20,0 | Стратегия №5 | 13,0 | 16,9 | 23,0 | ||
| Стратегия №1 | 12,4 | 16,7 | 21,0 | Стратегия №1 | 13,6 | 20,0 | 24,2 | ||
| Стратегия №2 | 17,0 | 15,6 | 17,1 | Стратегия №2 | 18,7 | 18,7 | 19,7 | ||
| Стратегия №3 | 16,3 | 16,8 | 19,5 | Стратегия №3 | 17,9 | 20,2 | 22,4 | ||
| Стратегия №4 | 16,5 | 17,6 | 20,3 | Стратегия №4 | 18,2 | 21,1 | 23,3 | ||
| Стратегия №5 | 11,5 | 13,8 | 20,0 | Стратегия №5 | 12,7 | 16,6 | 23,0 | ||
| Стратегия №1 | 11,1 | 17,1 | 20,9 | Стратегия №1 | 12,7 | 15,2 | 18,2 | ||
| Стратегия №2 | 15,0 | 16,0 | 17,3 | Стратегия №2 | 10,5 | 14,8 | 20,5 | ||
| Стратегия №3 | 14,3 | 17,3 | 19,4 | Стратегия №3 | 15,7 | 20,7 | 22,3 | ||
| Стратегия №4 | 16,6 | 17,6 | 20,2 | Стратегия №4 | 18,3 | 21,1 | 23,2 | ||
| Стратегия №5 | 11,7 | 14,0 | 20,0 | Стратегия №5 | 12,8 | 16,7 | 23,0 | ||
| Стратегия №1 | 11,8 | 16,9 | 25,1 | Стратегия №1 | 13,2 | 17,6 | 21,2 | ||
| Стратегия №2 | 16,0 | 15,8 | 20,6 | Стратегия №2 | 14,6 | 16,8 | 20,1 | ||
| Стратегия №3 | 15,3 | 17,1 | 23,3 | Стратегия №3 | 16,8 | 20,4 | 22,4 | ||
| Стратегия №4 | 16,6 | 17,6 | 24,3 | Стратегия №4 | 18,2 | 21,1 | 23,3 | ||
| Стратегия №5 | 11,6 | 13,9 | 20,0 | Стратегия №5 | 12,7 | 16,6 | 23,0 | ||
| Стратегия №1 | 11,5 | 17,0 | 23,0 | Стратегия №1 | 13,0 | 16,4 | 19,7 | ||
| Стратегия №2 | 15,5 | 15,9 | 19,0 | Стратегия №2 | 12,6 | 15,8 | 20,3 | ||
| Стратегия №3 | 14,8 | 17,2 | 21,4 | Стратегия №3 | 16,3 | 20,6 | 22,4 | ||
| Стратегия №4 | 16,6 | 17,6 | 22,3 | Стратегия №4 | 18,3 | 21,1 | 23,3 | ||
| Стратегия №5 | 11,7 | 14,0 | 20,0 | Стратегия №5 | 12,8 | 16,7 | 23,0 | ||
| Стратегия №1 | 11,7 | 17,0 | 24,1 | Стратегия №1 | 13,1 | 17,0 | 20,5 | ||
| Стратегия №2 | 15,8 | 15,9 | 19,8 | Стратегия №2 | 17,4 | 19,1 | 22,8 | ||
| Стратегия №3 | 15,1 | 17,2 | 22,4 | Стратегия №3 | 16,6 | 20,6 | 25,8 | ||
| Стратегия №4 | 16,6 | 17,6 | 23,3 | Стратегия №4 | 18,3 | 21,1 | 26,8 | ||
| Стратегия №5 | 11,7 | 14,0 | 20,0 | Стратегия №5 | 12,9 | 16,8 | 23,0 |
Вопросы для самоконтроля
1. Раскройте понятие риска и неопределенности.
2. Запишите формулу выбора стратегии по критерию Вальда.
3. Раскройте алгоритм выбора стратегии по критерию Вальда.
4. Запишите формулу выбора стратегии по критерию нейтрального игрока.
5. Раскройте алгоритм выбора стратегии по критерию нейтрального игрока.
6. Запишите формулу выбора стратегии по критерию азартного игрока.
7. Раскройте алгоритм выбора стратегии по критерию азартного игрока.
8. Запишите формулу выбора стратегии по критерию Сэвиджа.
9. Раскройте алгоритм выбора стратегии по критерию Сэвиджа.
10. Запишите формулу выбора стратегии по критерию Гурвица.
11. Раскройте алгоритм выбора стратегии по критерию Гурвица.