Пример: ряд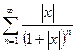 
является рядом геометрической прогрессии с первым членом 
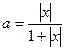и знаменателем 
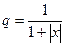. Если 
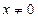, то 
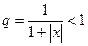и ряд в этих точках сходится. Сумма функционального ряда в этих точках будет равна: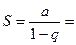 
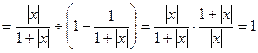. С другой стороны, если 
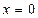, то соответствующий числовой ряд тоже сходится и его сумма будет равна 0. Т.о., получаем, что областью
сх-сти данного ряда является вся числовая ось, а его суммой – функция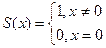 
. Эта функция в точке 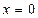терпит разрыв, хотя все функции 
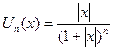в этой точке непрерывны.
Пусть дана некоторая пос-ть функций с общей обл.опр. Х: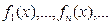 
(3).
Придавая переменной х значения х0 получим некоторую числовую пос-ть: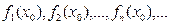 
(4). Мн-во D тех значений х0, для которых числовая пос-ть (4) сходится, называется областью сходимости функ-ной пос-ти (3). Ф-ю 
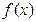, опред-ную в области D и принимающую в каждой точке х0 этой области значение 
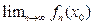назыв. пределом функциональной пос-ти (3).
Сумму функ-го ряда можно ввести иначе: как предел некоторой функ-ной пос-ти. Действительно, запишем пос-ть функций: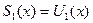 
, 
, 
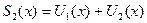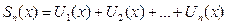. Придавая переменной х значение 
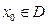, получим числовую пос-ть 
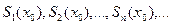. Это будет пос-ть частичных сумм числового ряда 
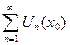. Пусть 
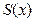- сумма ряда 
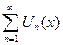. Тогда 
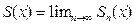, т.е. для любого 
, 
.
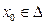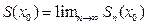По определению это означает, что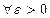 
.
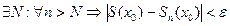В общем случае номер N зависит от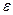 
и от х0
df: (равномерная сх-ть) Есл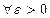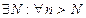и 
и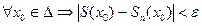 
, то говорят, что ряд 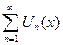сходится в области Δ равномерно.
th: (признак равномерной сходимости Вейерштрасса). Если найдется сходящийся числовой ряд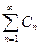 
такой, что 
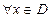выполняется н-во 
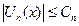, n =1,2,3,… (6), то функ. ряд 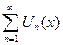сходится в области D равномерно.
Если для функ. ряда 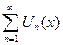в области D выполняется н-во (6), то говорят, что функ. ряд 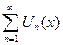мажорируется в области D числовым рядом 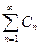. Ряд 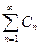называют при этом мажорирующим рядом (или мажорантой).
Замечание: признак Вейерштрасса достаточный, но не необходимый, т.е. существуют равномерно сходящиеся ряды, для которых не удается подобрать мажорирующего ряда. Равномерно сходящиеся ряды, для которых можно найти мажорирующий сходящийся ряд, часто называют правильно сходящимися.
Свойства равномерно сходящихся рядов:
1) Если ряд 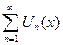сходится в области D равномерно и все члены ряда в этой области непрерывны, то сумма ряда 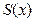тоже будет непрерывна в области D.
2) Если ряд 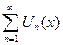сходится в области D равномерно и все члены ряда в этой области непрерывны, то 
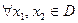ряд 
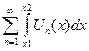сходится в области D равномерно, и справедливо неравенство: 
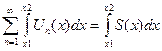(7), где 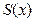- сумма ряда .
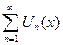Замечание: Так как 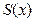- сумма ряда 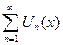, то можно записать 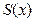= 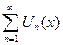. Но тогда неравенство (7) можно переписать в виде: 
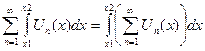, поэтому говорят, что равномерно сходящийся ряд непрерывных функций можно почленно интегрировать на любом отрезке 
.
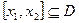3) Пусть ряд 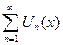сходится в области D и 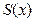- его сумма. Если все члены этого ряда в области D непрерывно дифференцируемы и ряд 
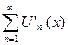сходится в D равномерно, то ряд 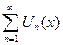тоже сходится в области D равномерно, и его сумма является функцией непрерывно дифференцируемой и имеет место равенство 
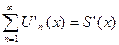(8).
Замечание: Равенство (8) можно записать в виде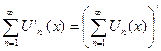 
. Поэтому говорят, что если ряд производных сходится в области D равномерно, то исходный ряд тоже сходится в D равномерно и его можно почленно дифференцировать.
4) Пусть ряд 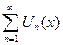сходится в области D равномерно. Если 
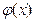- ограниченная в области D функция, то ряд 
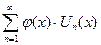тоже будет сходиться в области D равномерно
Степенной ряд.
df: (определение)Степенным рядом по степени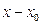 
называют функциональный ряд вида 
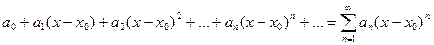, (1) где 
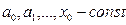, а - коэфф. степенного ряда. Если 
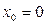, то 
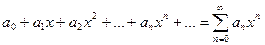(2)
Ряд называется степенным рядом по степени х.