ОГЛАВЛЕНИЕ
| Введение…..………………………………….………………………….… | ||
| 1. | Матричная алгебра…… ………...………………………………………... | |
| 1.1. | Матрицы……………………….…………..……………………………… | |
| 1.2. | Действия над матрицами……….………….……………………………... | |
| 1.3. | Определители…….………………………..……………………………… | |
| 1.4. | Свойства определителей…………………….…………………………… | |
| 1.5. | Обратная матрица…………………………..…………………………….. | |
| 2. | Системы линейных уравнений………….…………………………….…. | |
| 2.1. | Решение систем линейных уравнений……..………...……………….…. | |
| 2.2. | Модель Леонтьева многоотраслевой экономики…….……………….… | |
| Задания для контрольной работы…….……………………………….…. | ||
| Правила выполнения и оформления контрольных работ………………. | ||
| Библиографический список…………………………..……………….….. |
ВВЕДЕНИЕ
Современная концепция высшего экономического образования достаточно полно реализует специфику изучения математических дисциплин. Цикл математических дисциплин для бакалавриата согласно Государственному стандарту высшего профессионального образования состоит из ряда взаимосвязанных разделов с иллюстрацией их применения в экономике. К ним относится линейная алгебра и ее приложения в задачах оптимизации.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов, так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное компактной форме. Один из важнейших разделов линейной алгебры – системы линейных уравнений – являются одним из основных инструментов математического моделирования экономических процессов.
Математика является не только мощным средством для решения прикладных задач и универсальным языком науки, но и элементом общей культуры. В связи с этим математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного экономиста.
МАТРИЧНАЯ АЛГЕБРА
Матрицы
Прямоугольная таблица чисел, содержащая 
строк и 
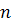столбцов, называется матрицей 
:
,
где 
– действительные числа 
, называемые элементами матрицы, 
и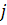 
– соответственно индексы строки и столбца.
Две матрицы называются равными, если числа их строк и столбцов равны и если равны элементы, расположенные на соответствующих местах этих матриц. Матрица называется нулевой, если все ее элементы равны нулю.
Если число столбцов матрицы 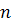равно числу ее строк, то матрицу называют квадратной матрицей порядка 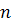. Элементы 
квадратной матрицы порядка 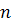образуют ее главную диагональ. Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю. Диагональная матрица называется единичной, если все ее элементы, расположенные на главной диагонали, равны единицы. Например,
соответственно квадратная, диагональная и единичная матрицы третьего порядка.
Действия над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичные операциям над числами, а некоторые – специфические.
Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число. Например,
.
Суммой матриц 
и 
одинаковых размерностей называется матрица, элементы которой равны сумме элементов матриц А и В, расположенных на соответствующих местах. Например,
.
Пример 1. В некоторой отрасли 4 завода выпускают 3 вида продукции. Матрица задает объемы продукции на каждом заводе в первом квартале, матрица – во втором; 
– объемы продукции -го типа на -ом заводе в первом и втором кварталах соответственно: 
.
Найти: а) объемы продукции; б) прирост объемов производства во втором квартале по сравнению с первым по видам продукции и заводам.
Решение. а) Объемы продукции за полугодие определяются суммой матриц А и В, т.е. 
, где 
– объемы продукции -го типа, произведенный за полугодие -ым заводом.
б) Прирост во втором квартале по сравнению с первым определяется разностью матриц 
.
Отрицательные элементы 
матрицы 
показывают, что на данном заводе объем производства -го продукта уменьшился; положительные – увеличился; нулевые – не изменился.
Умножение матрицы на матрицу определено, когда число первой равно числу строк второй. При этом произведением матрицы А порядка 
на матрицу В порядка 
называется матрица 
порядка , элементы 
которой вычисляются как сумма произведений элементов -ой строки матрицы и 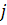-го столбца матрицы :
.
Пример 2. Вычислить произведение матриц А и В, где
.
Решение. По определению находим элементы матрицы 
как произведение соответствующих строки и столбца матриц и .
Пример 3. Предприятие производит 3 типа продукции, объемы выпуска заданы матрицей . Цена реализации единицы -го типа продукции в 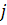-ом регионе задана матрицей . Число регионов, в которых реализуется продукция равно 4. Найти матрицу выручки по регионам, если
.
Решение. Выручка определяется матрицей 
, причем 
– это выручка предприятия в -ом регионе:
.
Пример 4. Предприятие производит 3 типа продукции, используя 4 вида ресурсов. Нормы затрат ресурса -го вида на производство единицы продукции 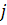-го типа заданы матрицей затрат . Значения стоимости каждого вида ресурса в расчете на единицу заданы матрицей 
. Пусть за определенный промежуток времени предприятие выпустило количество продукции каждого типа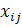 
, заданное матрицей 
.
Определить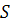 
– матрицу полных затрат ресурсов каждого вида на производство всей продукции за данный период времени и полную стоимость всех затраченных ресурсов, если
.
Решение. Матрица полных затрат ресурсов 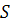определяется как произведение матриц и , т.е. 
.
Согласно условию задачи
,
т.е. за данный период времени будет израсходовано 930 ед. ресурса первого вида, 960 ед. ресурса второго вида, 450 ед. ресурса третьего вида и 630 ед. ресурса четвертого вида.
Стоимость всех затраченных ресурсов определяется как произведение матриц 
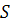и , или 
.
В данном случае 
Переход от матрицы к матрице 
, в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированием матрицы . Матрица называется транспонированной относительно матрицы . Например,
.
Определители
Определителем матрицы второго порядка называется число
.
Определителем матрицы третьего порядка называется число
.
Знаки, с которыми слагаемые входят в данную формулу, легко запомнить, пользуясь правилом треугольника. Определитель квадратной матрицы обозначается 
или det 
.
Пример 5. Вычислить определитель матрицы 
.
Решение. 
.
Введем понятие определителя произвольного порядка 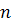. Для этого понадобятся следующие определения.
Минором 
элемента определителя -го порядка называется определитель 
-го порядка, который получается вычеркиванием в данном определителе строки и столбца, содержащих элемент . Алгебраическим дополнением 
элемента называется его минор, умноженный на 
:
.
Если например, 
,
то 
, 
.
Известно, что каждый определитель равен сумме произведений любой его строки или столбца на их алгебраические дополнения, то есть
= 
,
= 
.
Эти равенства называются соответственно разложениями определителя матрицы по элементам -ой строки и 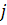-го столбца. Данные формулы применяются для вычисления определителей матриц.
Пример 6. Вычислить определитель матрицы 
.
Решение. Разложим данный определитель по элементам его третьего столбца.
= 
.
Свойства определителей
Вычисление определителя с помощью разложения по строке или столбцу – достаточно трудоемкое дело. Используя свойства определителя, можно значительно упростить его вычисление.
1) При транспонировании матрицы ее определитель не меняется, то есть 
.
2) Общий множитель всех элементов строки или столбца определителя можно вынести за знак определителя. Например,
.
3) Если элементы какой-нибудь строки (столбца) определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. Например,
.
4) Определитель, содержащий две одинаковые строки или столбца, равен нулю.
5) Определитель не изменится, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число. Например,
.
6) Определитель произведения двух квадратных матриц равен произведению их определителей: 
.
Если в определителе порядка 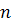имеется столбец (строка), все элементы которого, кроме одного, равны нулю, то, разложив определитель по этому столбцу (строке) мы сведем его к вычислению определителя порядка . Если же столбца (строки) нет, то, используя свойство 5) определителей, можно, не меняя значения данного определителя, преобразовать его так, чтобы в выбранном столбце (строке) все элементы, кроме одного, обратились в нуль.
Пример 7. Вычислить определитель матрицы 
.
Решение. Преобразуем матрицу так, чтобы все элементы третьей строки, кроме одного, обратились в нуль. Для этого домножим третий столбец на -4 и добавим к первому, а затем домножим третий столбец на 2 и добавим ко второму.
.
Обнулим в полученном определителе третьего порядка все элементы второй строки, кроме одного. Для этого домножим третий столбец нового определителя на -13 и 4 и добавим соответственно к первому и второму столбцам.
.
Обратная матрица
Матрица 
называется обратной для квадратной матрицы , если 
.
Квадратная матрица имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Такие матрицы называются невырожденными. Невырожденная матрица имеет единственную обратную
,
где 
– алгебраическое дополнение элемента матрицы .
Пример 8. Найти матрицу, обратную к матрице 
.
Решение. Вычислим определитель матрицы :
. Значит матрица невырожденная и имеет обратную. Находим
.
Для проверки правильности вычислений полезно убедиться, что для найденной матрицы верно равенство 
.
СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ