Занятие № 11.Тема.Наибольшее и наименьшее значение функции.
Мотивация.
«Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.
И я очень надеюсь, что каждый из вас вспомнит этот урок, когда столкнется с задачей на оптимизацию и навыки, полученные сегодня, Вам обязательно пригодятся.
Цели урока:
Образовательная – проверить степень усвоения студентами материала прошлого урока, вывести алгоритм нахождения наибольшего и наименьшего значений функции, формировать умения решать задачи на отыскание наибольших и наименьших значений функции.
Развивающая – развивать познавательный интерес студентов к дисциплине, умение исследовать, выделять главное, сравнивать, анализировать, делать выводы.
Воспитательная – воспитывать умения планировать свою деятельность; бережно относиться к материальным ценностям; содержать в порядке рабочее место. Формировать опыт совместной деятельности, умение соблюдать элементарные правила и нормы устанавливаемой дисциплины и культуры общения.
Средства обучения: Алимов Ш А, Колягин Ю М и др. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений/ М.: Просвещение, 2017.
|
|
Изучение нового материала:
Пусть функция 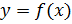 непрерывна на отрезке
непрерывна на отрезке 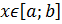 .
.
По теореме Вейерштрасса: если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
 Эти значения функция может принимать либо во внутренней точке
Эти значения функция может принимать либо во внутренней точке 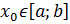 , либо на границе отрезка, т.е при
, либо на границе отрезка, т.е при 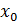 =
= 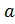 или
или 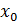 =
= 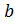 .
.
Если 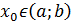 , то точку
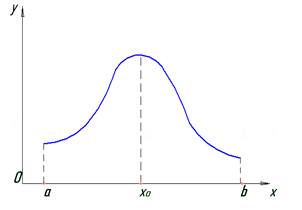
, то точку 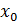 следует искать среди критических точек данной функции (точек, где производная равна нулю или не существует) (см. рис.1).
следует искать среди критических точек данной функции (точек, где производная равна нулю или не существует) (см. рис.1).
Рис.1
Правило нахождения наибольшего и наименьшего
значений функции на 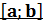 (записать в опорный конспект)
(записать в опорный конспект)
Найти критические точки функции, принадлежащие данному отрезку.
2. Вычислить значения функции в найденных критических точках и на концах отрезка, т.е. в точках 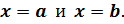
Сравнить все полученные значения функции и выбрать из них наименьшее и наибольшее.
Замечание 1. Если функция 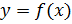 на отрезке
на отрезке 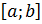 имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
На рисунке 1 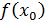 = fнаиб = fmax (наиб – наибольшее, max - максимальное).
= fнаиб = fmax (наиб – наибольшее, max - максимальное).
Замечание 2. Если функция 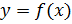 на отрезке
на отрезке 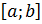 не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее на другом.
не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее на другом.
Замечание 3. Если 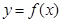 - периодическая непрерывная на интервале
- периодическая непрерывная на интервале 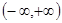 функция, то она достигает своего наибольшего значения в бесконечном числе точек максимума и наименьшего значения в бесконечном числе точек минимума.
функция, то она достигает своего наибольшего значения в бесконечном числе точек максимума и наименьшего значения в бесконечном числе точек минимума.
|
|