LECTURE 1
Matrices. Operations over matrices.
Definition of a numerical matrix. Classification of matrices.
A numerical matrix of dimension m ´ n is a rectangular table of numbers consisting of «m »horizontal lines (rows) and «n » vertical lines (columns).
It has the following form:
The numbers 
(i = 1, 2, …, m; j= 1, 2, …, n) are called elements of the matrix.
The index «i » denotes the number of a matrix row, the index «j » – the number of a matrix column.
In general, objects of an arbitrary nature can be elements of a matrix.
Examples: A(3; 2) = 
; A(2; 4) = 
.
If n = 1, a matrix А(m; 1) is called a column matrix (or a matrix-column).
It has the following form:
А(m; 1) = 
. For example, А(3;1) = 
.
If m = 1, a matrixА(1; n) is called a row matrix (or a matrix-row).
It has the following form: 
For example, 
If we replace all the rows by columns and vice versa in a matrix А(m; n) then the changed matrix is called the transposed matrix to the matrix А and it is denoted by 
:
.
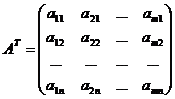If m = n, then a matrix А(n; n) is called a square matrix of the n- th order.
It has the following form: А (n; n) = 
In particular, for n = 2:
А(2; 2) = 
for n = 3: A(3; 3) = 
– square matrices of the second and the third order respectively.
The main diagonal of a square matrix A(n; n) is the diagonal consisting ofthe elements
, 
, 
, …, 
.
A diagonal matrix is a square matrix D (n; n) of which all the elements non-lying on the main diagonal are equal to zero.
It has the following form:
D(n; n) = 
.
An identity matrix is a diagonal matrix of which all the diagonal elements are equal to 1 (unity).
It has the following form:
E (n; n) = 
.
For example, E(2; 2) = 
; E(3; 3) = 
.
A zero matrix is a matrix of which all the elements are equal to zero.
It has the following form:
0 = 
.
A symmetric matrix is a square matrix of which the elements located symmetrically according to the main diagonal are equal each other, i.e.
а 
= а 
(i = 1, 2,…, n; k = 1, 2, …, n).
It has the following form:
С(n; n) =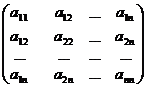 
.
In particular, С(2; 2) = 
.
Two matrices А(m; n) and B(m; n) of the same dimension are equal if all their corresponding elements are equal, i.e. 
= 
(i = 1, 2, …, m; k = 1, 2,…, n).
Matrices of different dimensions aren’t compared among themselves.
Operations over matrices
Linear operations over matrices are addition, subtraction of matrices and multiplication of matrices on a number.
a) Addition and subtraction of matrices are only defined for matrices of the same dimension, i.e. for matrices of the form:
А(m; n) = 
and В(m; n) = 
.
The sum (difference) of two matrices is a matrix С(m; n) = 
of which elements c are equal to the sum (difference) of the corresponding elements 
and , i.e. 
= 
(i = 1, 2, …, m; k = 1, 2, …, n). The sum (difference) of matrices is denoted by А 
В, i.e. С(m; n) = A(m; n) B(m; n), or in a developed form:
C (m; n) = 
= = 
.
Thus, the sum (difference) of two matrices is determined elementwise.
Example: 
+ 
= 
.
b) The product of a matrix А(m; n) on a number 
is the matrix obtained from the matrix А(m; n) by multiplying all its elements on l, i.e. the elements of the matrix B(m; n) are determined by the following formula: 
(i = 1, 2,…, m; k = 1, 2,…, n).
The product of a matrix А(m; n) on a number l is denoted by l А.
Thus: В(m; n) = l × A(m; n) or in a developed form:
= l 
= 
.
Example: 5 
= 
Multiplication of matrices
As against the operations of addition (subtraction) the operation of multiplication of a matrix on a matrix is determined by more complicated way.
We can speak on product of rectangular matrices A and B only if the number of columns of the first matrix A is equal to the number of rows of the second matrix B, and the number of rows of the matrix А×В is equal to the number of rows of the matrix A, the number of columns of the matrix А×В is equal to the number of columns of the matrix В.
The rule of multiplication of matrices can be formulated as follows: to receive an element standing in the i -th row and the k -th column of the product of two matrices, it is necessary the elements of the i -th row of the first matrix multiply on the corresponding elements of the k -th column of the second matrix and add the obtained products.
Let А(m; n) = ; B(n; k) = 
×
Then C(m; k) = A(m; n)×B(n; k) =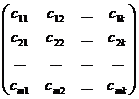 
, where cij are defined as follows:
… … … … … … … … … …
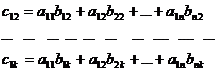
Examples:
1) 
× 
= 
= 
; 
2) 
× 
= 
= 
; 
3) 
= 
=
= 
The product of two matrices, generally speaking, depends on the order of multiplicands. It can even happen that the product of two matrices taken in one order will have sense, and the product of the same matrices taken in the opposite order will not have any sense.
Examples:
1) 
2) 
.
The identity matrix Е doesn’t change any elements of a matrix A by multiplying on the matrix A (if this multiplication is possible), i.e. А× Е = А or Е × А = А. If a matrix А is square and has the same dimension with Е then А × Е = Е × А = А.
Examples:
1) 
2) 
It is convenient to write down some economic dependencies by using matrices.
| Resources | Branches of economy | |
| the industry | Agriculture | |
| Electric power | 5,3 | 4,1 |
| Manpower | 2,8 | 2,1 |
| Water resources | 4,8 | 5,1 |
For example, the table of distribution of resources on separate branches of economy (in standard units) can be written down in the compact form as the matrix of distribution of resources on branches: 
In this record, for example, the matrix element a11 = 5,3 shows the consumption of electric power by the industry, and the element a22 = 2,1 – the consumption of manpower by the agriculture.
Example. An enterprise produces three kinds of production: P1, P2, P3 and uses a raw material of two types: S1 and S2. The norms of expense of the raw material are characterized by the matrix 
where each element aij (i = 1, 2, 3; j = 1, 2) shows the volume of units of the raw material of the j -th type spent for manufacturing a unit of production of the i -th kind. The plan of output is set by the matrix-row C = (100 80 130), the cost of the unit of each type of the raw material (monetary units) – by the matrix-column 
Determine the expenses of the raw material necessary for planned output and the total cost of the raw material.
Solution: The expenses of the first raw material make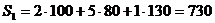 
units and of the second raw material – 
units, therefore the matrix-row of the expenses of the raw material S can be written down as the product 
Then the total cost of the raw material 
monetary units can be written in the matrix record: 
Glossary
matrix (plural – matrices) – матрица; numerical – числовой; row – строка; column – столбец
dimension – размерность; rectangular – прямоугольный; element – элемент
transposed matrix – транспонированная матрица; square matrix – квадратная матрица
main diagonal – главная диагональ; diagonal matrix – диагональная матрица
identity matrix – единичная матрица; zero matrix – нулевая матрица
symmetric matrix – симметрическая матрица; addition – сложение; subtraction – вычитание
to obtain – получать; manpower – трудовые (людские) ресурсы; raw material – сырье; expenses – затраты
output – выпуск продукции; total cost – общая стоимость
Exercises for Seminar 1
1.1. Let 
Find C = 3A + 2B and D = 4B – 5A.
1.2. Let 
Find AB and BA if possible.
1.3. Find A3 if 
1.4. Let 
Find AB and BA if possible.
1.5. Compute: a) 
b) 
c) 
d) 
e) 
1.6. Find the matrix X for which A + 2X = 3B if
1.7. Show that the matrix 
is a root of the following polynomial:
P(X) = X 3 – 6X 2 + 8X – 9.
1.8. Multiply the following matrices:
a)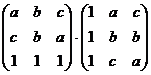 
; b) 
.
1.9. Find the following matrices: a) 
; b) 
.
1.10. Compute 
where 
, and is the matrix transposed to 
.