Задача №3
Обработка статистических данных проката колёсных пар электрического подвижного состава.
Вариант 11
Используя данные задания, построить зависимость плотности распределения проката и выполнить расчеты:
1) Среднего значения проката колёсных пар.
2) Дисперсии проката.
3) Среднеквадратичного отклонения проката.
Среднее значение проката колесных пар определяется выражением:
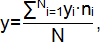
где yi-результаты i-го измерения проката колёсной пары при данном пробеге локомотива;
ni- количество замеров проката с результатом yi.
N-общее число замеров проката при данном пробеге локомотива.
Дисперсия проката определяется по формуле:
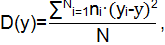
Среднеквадратичное отклонение проката определяется выражением:
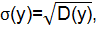
Плотность распределения проката определяется следующим образом:
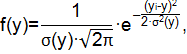
Результаты расчетов сведены в таблицу 1.
Результаты расчетов
Таблица 1
| № п/п | Прокат, мм | Число измерений | Среднее значение проката К.П. | Дисперсия проката | Среднеквадра-тичное отклонение проката | Плотность распределения проката |
| yi | ni |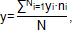 
| 
| 
| 
| |
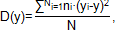
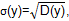
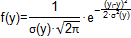
| 2,6 | 3,072 | 0,091 | 0,302 | 0,391 | ||
| 2,8 | 0,88 | |||||
| 2,9 | 1,122 | |||||
| 1,282 | ||||||
| 3,3 | 0,993 | |||||
| 3,4 | 0,733 | |||||
| 3,5 | 0,485 |
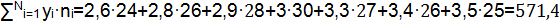
N=24+26+28+30+27+26+25=186;
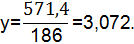
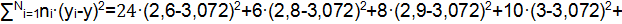
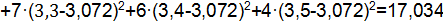
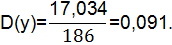
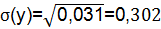
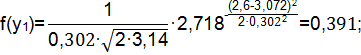
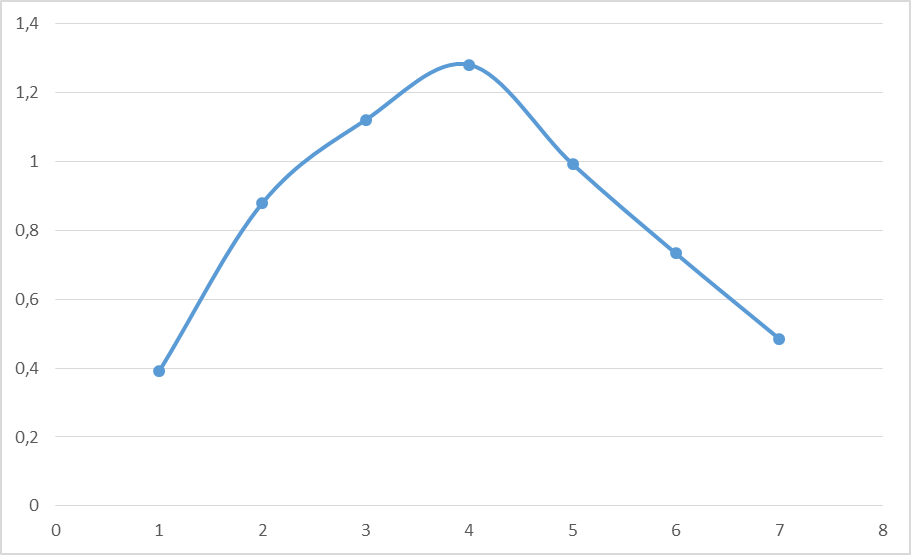
Результаты расчетов сведены в таблицу 1 и представлены в виде графика зависимости плотности распределения проката колеса (см. рис. 1).
f(y)
y, мм
Рис.1- График зависимости плотности распределения проката колеса.
Задача №4
Определение параметра потока отказов
Вариант 11
Используя данные задания выполнить расчет параметра потока отказов и построить зависимость ωi(ΔL).
Оценка параметра потока отказов рассчитывается при группировке отказов в интервалах наработки:
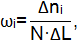
где i=1,2,3,4,5…k- номер интервала;
Δni- число отказов в интервале наработки;
N- число наблюдаемых объектов, N=1800;
ΔL- пробег, на котором велось наблюдение за объектами.
Результаты расчетов
Таблица 2
| Пробег, на котором велось наблюдение за объектами | Число отказов в интервале наработки | Параметр потока отказов |
| ΔL, км | Δni |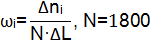 
|
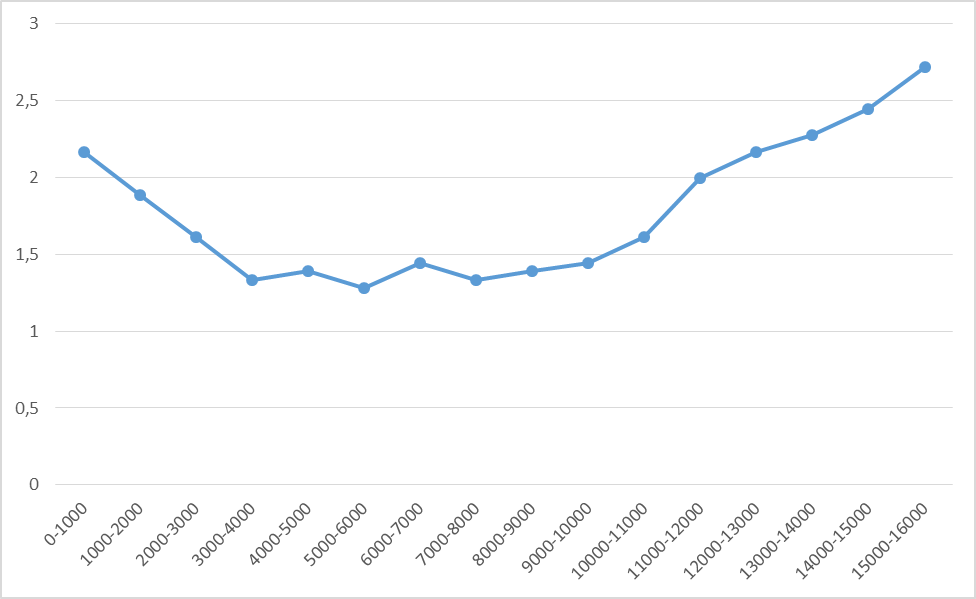
| 0-1000 | 2,167 | |
| 1000-2000 | 1,889 | |
| 2000-3000 | 1,611 | |
| 3000-4000 | 1,333 | |
| 4000-5000 | 1,389 | |
| 5000-6000 | 1,278 | |
| 6000-7000 | 1,444 | |
| 7000-8000 | 1,333 | |
| 8000-9000 | 1,389 | |
| 9000-10000 | 1,444 | |
| 10000-11000 | 1,611 | |
| 11000-12000 | ||
| 12000-13000 | 2,167 | |
| 13000-14000 | 2,278 | |
| 14000-15000 | 2,444 | |
| 15000-16000 | 2,722 |
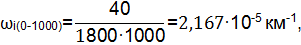
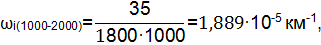
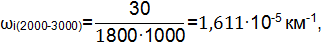
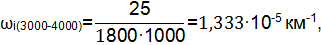
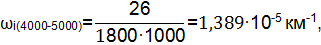
Результаты расчетов сведены в таблицу №2 и отражены в виде графика (см. рис. 2.).
ωiх10-5
ΔL, км.
Рис. 2 - График зависимости параметров потока отказов от пробега, на котором велось наблюдение за объектами ωi(ΔL).
Задание №5
Расчет зависимости числовых характеристик контролируемых параметров от пробега
Вариант 11
Используя данные задания определить аналитическую зависимость изменения контрольного параметра y от пробега l.
В результате распределения и расчета закона числовых характеристик контролируемого параметра для значений пробегов, при которых производились замеры, получаем зависимость числовых характеристик от пробега. Для номинального закона распределения это зависимость среднего контролируемого параметра от наработки и зависимость среднеквадратичного отклонения контролируемого параметра от наработки.
С помощью аналитической зависимости прогнозируется процесс изнашивания. График изменения контролируемого параметра y от пробега l имеет три периода.
Замеры контролируемого параметра производятся в период нормальной эксплуатации, в котором зависимость y(l) линейная. Поэтому предполагают, что зависимость числовых характеристик от пробега в интервале от первого до последнего замера также имеет линейный вид. Аппроксимацию экспериментальных данных осуществляют теоретической функцией так, чтобы свести к минимуму сумму квадратов отклонений эмпирических точек от искомой теоретической зависимости.
Исходные данные
Таблица 3
| № п/п | Пробег l, тыс. км. | Прокат y, мм. |
| 1,2 | ||
| 2,2 | ||
| 3,2 | ||
| 4,2 |
Цель: определить значения «а» и «b» уравнения y=а·l+b.
Математическое ожидание величины l:
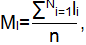
Математическое ожидание величины y:
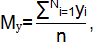
Второй смешанный момент:
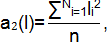
Второй смешанный начальный момент:
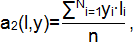
b=Мy-a·Ml,
Расчеты:
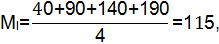
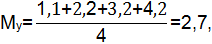
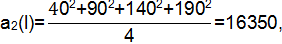
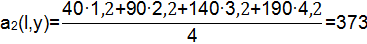
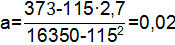
b=2,7-0,02·115=0,4
Тогда уравнение примет вид:
y=0,02·l-0,4.
Откуда находим:
y1=0,02·40-0,4=0,4
y2=0,02·90-0,4=1,4
y3=0,02·140-0,4=2,4
y4=0,02·190-0,4=3,4
Результаты расчетов наглядно отражены графически (см. рис. 3).
y,мм
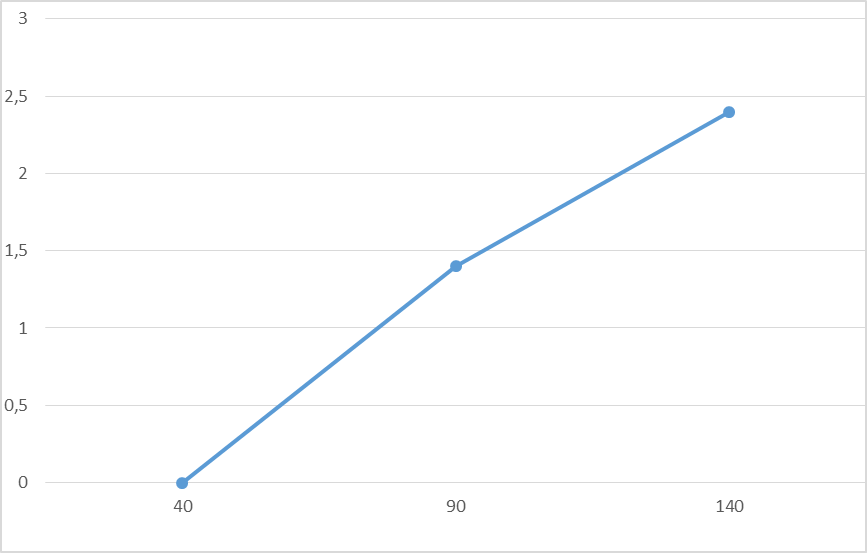
l, тыс. км.
Рис. 3 - Тренд диагностического параметра от пробега.
Задание №6
Проверка согласованности теоретического и статистического распределения
Вариант 11
Используя данные задания рассчитать статистическую вероятность события. Результаты расчетов свести в таблицу.
Рассчитать статистические значения вероятности отказа Q̅(t) и вероятность безотказной работы P ̅(t)=1-Q̅(t).
Рассчитать значения теоретической функции вероятности безотказной работы P̅(t).
Рассчитать значения Q̅(t), P̅(t) и P(t). Свести данные в таблицу
Построить P̅(t) и P(t) на графике.
Проверить возможность аппроксимации P̅(t) функцией P(t) по кривой согласия К. Пирсона.
Исходные данные для расчета
Таблица 4
| Количество систем, N | Δti, ч | n(Δti) |
| 0-5 | ||
| 5-10 | ||
| 10-15 | ||
| 15-20 | ||
| 20-25 | ||
| 25-30 | ||
| 30-35 | ||
| 35-40 | ||
| 40-45 | ||
| 45-50 | ||
| 50-55 | ||
| 55-60 | ||
| 60-65 | ||
| 65-70 | ||
| 70-75 | ||
| 75-80 |
Считать, что для рассматриваемых систем управления справедлив экспоненциальный закон надежности.
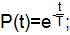
где Т=17,1 ч.
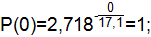
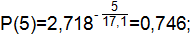
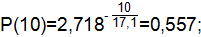
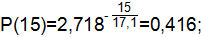
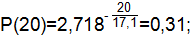
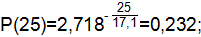
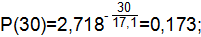
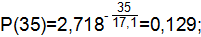
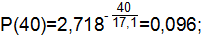
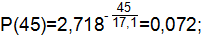
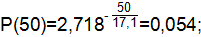
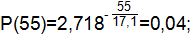
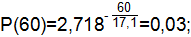
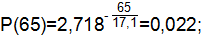
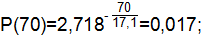
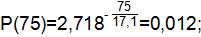
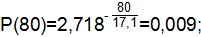
Статистическая вероятность событий определяется по формуле:
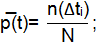
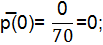
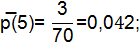
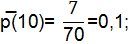
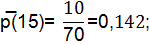
P ̅(t)=1-Q̅(t).
Отсюда:
Q̅(t)=1-P ̅(t);
Q̅(0)=1-0=1;
Q̅(5)=1-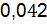 
=0,957;
Q̅(10)=1-0,1=0,9;
Q̅(15)=1-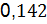 
=0,857;
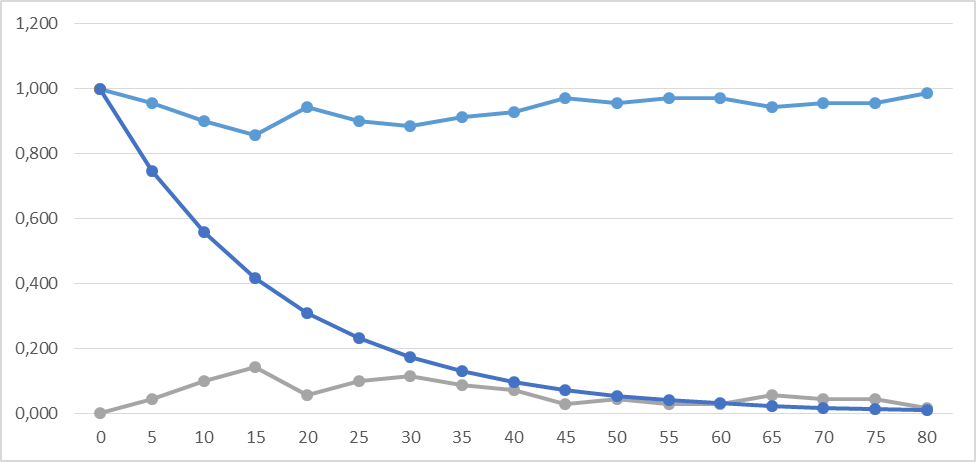
Результаты расчетов сведены в таблицу 5 и представлены в виде графиков (см рис. 4).
Результаты расчетов значений вероятностей отказов Q̅(t), статистических вероятностей событий Р̅(t) и кривой согласия К. Пирсона Р(t)
Таблица 5
| t | n(Δti) | Q̅ | Р̅ | P |
| 0,000 | ||||
| 0,957 | 0,043 | 0,746 | ||
| 0,900 | 0,100 | 0,557 | ||
| 0,857 | 0,143 | 0,416 | ||
| 0,943 | 0,057 | 0,31 | ||
| 0,900 | 0,100 | 0,232 | ||
| 0,886 | 0,114 | 0,173 | ||
| 0,914 | 0,086 | 0,129 | ||
| 0,929 | 0,071 | 0,096 | ||
| 0,971 | 0,029 | 0,072 | ||
| 0,957 | 0,043 | 0,054 | ||
| 0,971 | 0,029 | 0,04 | ||
| 0,971 | 0,029 | 0,03 | ||
| 0,943 | 0,057 | 0,022 | ||
| 0,957 | 0,043 | 0,017 | ||
| 0,957 | 0,043 | 0,012 | ||
| 0,986 | 0,014 | 0,009 |
Результаты расчетов представлены в виде графиков, показанных на рисунке 4.
t
Рис. 4.- График зависимости Q̅(t), Р̅(t), Р(t).
Проверяя согласованность теоретического и статистического распределений, исходят из расхождений между теоретическими вероятностями pi и статистическими вероятностями событий p̅i. При этом мера расхождения обозначается Х2.
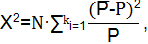
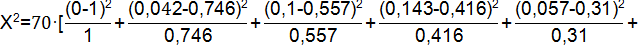
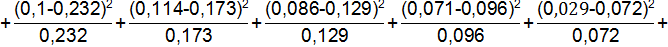
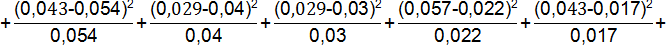
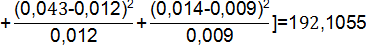
Число степеней свободы определяется по формуле:
r=k-s
где r - число степеней свободы;
k - число разрядов;
s – число независимых условий («связей»).
r=16-3=13
Используя таблицу значений мер расхождений Х2 получим, что величина, имеющая распределение Х2 с r степенями свободы превзойдет данное значение Х2 с вероятностью 0,001. Следовательно, гипотеза применяется как неправдоподобная.
Задача №7