Центром тяжести твердого тела называется геометрическая точка, являющаяся центром параллельных сил тяжести, действующих на все частицы тела. Для абсолютно твердого тела положение центра тяжести относительно тела является неизменным.
Равнодействующую сил тяжести р1,р2,...,рп, действующих на все частицы данного тела, обозначим Р. Модуль этой силы называется весом тела и определяется равенством
Координаты центра тяжести, как центра параллельных сил, определяются формулами (5.3):
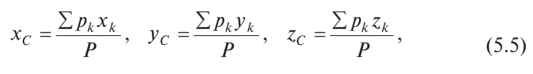
где хк, ук, zk — координаты точек приложения сил тяжести рк, действующих на к-е частицы тела.
Если тело является однородным, то вес рк любой его части пропорционален объему vk этой части тела: рк = yvk, где у — вес единицы объема. Подставив эти значения в формулы (5.5), после сокращения на у получим координаты точки С, называемой центром тяжести объема V:
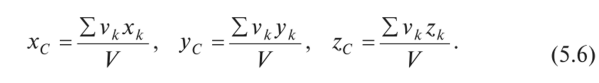
Аналогичные рассуждения можно провести для тела, представляющего собой однородную плоскую пластину, площадь которой равна S, и определить координаты ее центра тяжести:
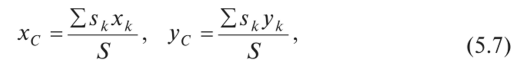
где S — площадь всей пластины; sk — площади частей, из которых состоит пластина; хк, ук — координаты центров тяжести площади к -й части пластины.
Точно так же получаются координаты центра тяжести линии:
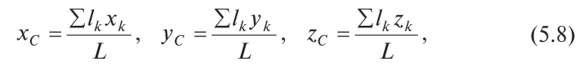
где L — длина всей линии; 1к — длина ее к-х частей.
Анализируя формулы (5.6) — (5.8), приходим к выводу, что центр тяжести однородного тела зависит только от его геометрической формы. Исходя из структуры расчетных формул, можно обосновать: если однородное тело имеет плоскость, ось или центр симметрии, тоa его центр тяжести расположен соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.
Действительно, если однородное тело имеет плоскость симметрии, то этой плоскостью оно разбивается на две такие части, веса которых /?) и р2 равны друг другу, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Тогда, направив, например, ось х перпендикулярно плоскости симметрии и выбрав начало отсчета координаты х в точке пересечения оси х и плоскости симметрии, будем иметь для двух симметричных частей тела соотношения р{ — р2, х, = — х2. Подставив их в первую из формул (5.5), получим хс= 0, т. е. центр тяжести всего тела расположен в плоскости симметрии тела.
|
|
На основе изложенного можно легко установить, что:
· 1) центр тяжести отрезка прямой лежит в его середине;
· 2) центры тяжести окружности, площади крута, однородного круглого кольца, поверхности и объема шара находятся в их геометрических центрах;
· 3) центры тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения диагоналей соответствующих фигур.
Методика определения центра тяжести тел состоит в следующем. Тело разбивается на конечное число таких частей, для каждой из которых положение центра тяжести известно или может быть предварительно определено. Далее центр тяжести всего тела вычисляют по общим формулам (5.5) — (5.8), подставляя в них соответствующие параметры тех частей, на которые было разбито тело.
Таким образом, исследуемое тело рассматривается в качестве суммы простейших тел. Иногда его можно представить как разность тел (большего с вычетом меньшего). Тогда при расчетах вес (объем, площадь) большего тела считают положительным, а вес (объем, площадь) меньшего тела, как вычитаемого, считают отрицательным; так поступают для тел, имеющих вырезы, отверстия.
|
|
Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то его разбивают на бесконечное число элементарных частей, и тогда стоящие в формулах (5.5) — (5.8) суммы обращаются в интегралы.
Центр параллельных сил
Рассмотрим две параллельные, направленные в одну сторону силы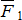 
, и 
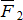, приложенные к телу в точках А 1 и А 2 (рис.6.1). Эта система сил имеет равнодействующую 
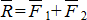, линия действия которой проходит через некоторую точку С. Положение точки С можно найти с помощью теоремы Вариньона:
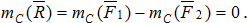
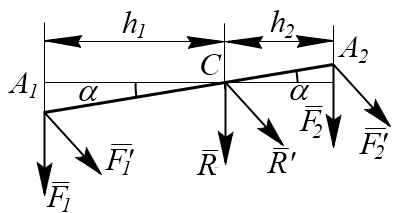
Рис.6.1
Если повернуть силы 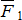и 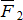около точек А 1 и А 2 в одну сторону и на один и тот же угол, то получим новую систему параллельных сал, имеющих те же модули. При этом их равнодействующая будет также проходить через точку С. Такая точка называется центром параллельных сил.
Рассмотрим систему параллельных и одинаково направленных сил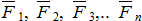 
, приложенных к твердому телу в точках 
.
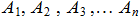Эта система имеет равнодействующую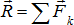 
.
Если каждую силу системы повернуть около точек их приложения в одну и ту же сторону и на один и тот же угол, то получатся новые системы одинаково направленных параллельных сил с теми же модулями и точками приложения. Равнодействующая таких систем будет иметь тот же модуль R, но всякий раз другое направление. Сложив силы F 1 и F 2 найдем что их равнодействующая R 1, которая всегда будет проходить через точку С 1, положение которой определяется равенством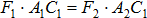 
.
|
|
Сложив далее R 1 и F 3, найдем их равнодействующую, которая всегда будет проходить через точку С 2, лежащую на прямой А 3 С 2. Доведя процесс сложения сил до конца придем к выводу, что равнодействующая всех сил действительно всегда будет проходить через одну и ту же точку С, положение которой по отношению к точкам 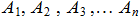будет неизменным.
Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол называется центром параллельных сил (рис. 6.2).
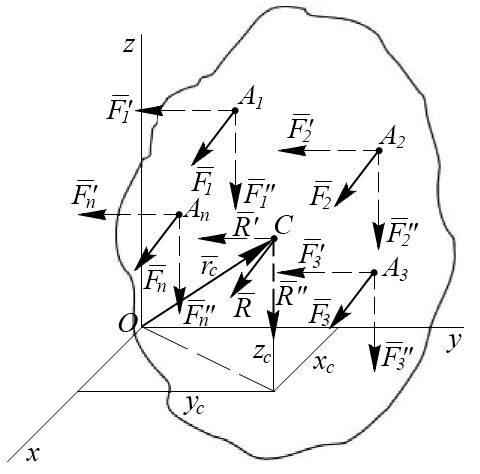
Рис.6.2
Определим координаты центра параллельных сил. Поскольку положение точки С по отношению к телу является неизменным, то ее координаты от выбора системы координат не зависят. Повернем все силы около их приложения так, чтобы они стали параллельны оси Оу и применим к повернутым силам теорему Вариньона. Так как R' является равнодействующей этих сил, то, согласно теореме Вариньона, имеем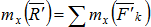 
, т.к. 
, 
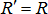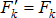, получим
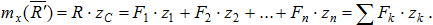
Отсюда находим координату центра параллельных сил zc:
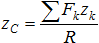
Для определения координаты xc составим выражение момента сил относительно оси Oz.
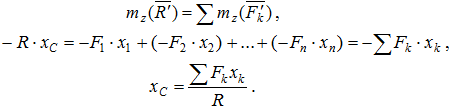
Для определения координаты yc повернем все силы, чтобы они стали параллельны оси Oz.
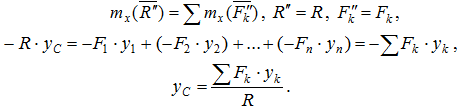
Положение центра параллельных сил относительно начала координат (рис. 6.2) можно определить его радиусом-вектором:
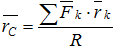
Домашнее задание:
1. Прочитайте конспект
2. Запишите определение координат центра параллельных сил