« Прикладная математика (без профиля)»
Разработано:
Ст. преподавателем Мирошниковой Е.Н.
Утверждено
на заседании кафедры
«___»____________ 20г.
Москва - 2015г.
1. Целью выполнения лабораторной работы является:
Закрепление теоретических сведений о математическом описании систем автоматического управления. Применение теоретических сведений о формах и способах описания систем на практике с помощью программы Mathcad, построение динамических характеристик в программе Mathcad.
2. Теория и методические указания
2.1 Математическое описание линейных систем
Для описания линейных систем могут применяться несколько способов:
- дифференциальные уравнения;
- модели в пространстве состояний;
- передаточные функции;
- модели вида «нули-полюса».
Первые два способа называются временными, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только вход-выходные свойства (то есть, описывают динамику не полностью).
Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры.
Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений. Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения.
При описании рассматривается система автоматического управления (САУ), описываемая линейным (линеаризованным) дифференциальным уравнением вида:
(2.1)
где u (t) – входной процесс, y (t) – выходной процесс, ai, bj, (
) – постоянные коэффициенты, n, m – постоянные числа. В операторной форме выражение (2.1) может быть записано –
.
Здесь D – оператор дифференцирования 
. Отсюда преобразование “вход-выход” системы –
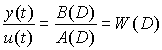, (2.2)
где W (D) называется операторной передаточной функцией.
Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:
, (2.3)
которая получается путем применения преобразования Лапласа к (2.2) при начальных нулевых условиях. Здесь s -комплексная переменная. Связь между операторной (2.2) и комплексной (2.3) передаточными функциями можно записать в виде
.
Комплексные числа, являющиеся корнями многочлена В (s), называются нулями передаточной функции, а корни многочлена A (s) – полюсами.
Явный вид связи входа и выхода определяется выражением:
, (2.4)
где w (t) – оригинал (т.е. полученный с помощью обратного преобразования Лапласа) комплексной передаточной функции W (s).
Линейное уравнение 
можно записать в операторной форме
или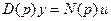 
где 
– входной сигнал, 
– сигнал выхода, 
– оператор дифференцирования, 
и 
– операторные полиномы.
Передаточная функция 
линейной стационарной системы от комплексной переменной 
определяется как отношение преобразования Лапласа выхода к преобразованию Лапласа входа при нулевых начальных условиях:
2.2 Временные и частотные характеристики звенев и систем
2.2.1 Временные характеристики звеньев и систем
Динамические свойства линейных звеньев и систем автоматического управления в целом могут быть описаны дифференциальными уравнениями и передаточными функциями, а также с помощью временных и частотных характеристик.
Временная характеристика представляет собой функцию времени, описывающую выходной сигнал звена (или системы) при подаче на вход звена определенного тестирующего сигнала. Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.
Указанные характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Переходные и частотные характеристики однозначно связаны с дифференциальным уравнением звена и его передаточной функцией и наряду с ними являются исчерпывающим описанием динамических свойств звена.
К числу основных временных характеристик звена или системы относятся переходная функция и функция веса.
Переходная функция звена представляет собой сигнал на выходе звена (реакцию звена), вызванный подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция, функция Хевисайда) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным (рисунок 2.2. 1).
Рисунок 2.2.1- Единичное ступенчатое воздействие
Единичное ступенчатое воздействие обозначается 
и может быть описано следующим выражением:
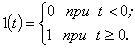(2.2.1)
Переходная функция обычно обозначается 
. Следовательно, – это выражение для 
при 
= .
Наряду с переходной функцией при описании звеньев и систем применяется функция веса, общепринятое обозначение которой 
. Эта временная характеристика представляет собой реакцию звена на дельта-функцию (единичную импульсную функцию, иглу Дирака). Дельта-функция, которая обозначается 
, – это математическая идеализация предельно короткого импульсного сигнала бесконечно большой амплитуды. Математически дельта-функцию можно описать следующим образом:
(2.2.2)
При этом согласно определению дельта-функции
. (2.2.3)
Таким образом, - это 
при = .
Поскольку дельта-функция равна производной по времени от единичного ступенчатого воздействия, то и между переходной функцией, и функцией веса линейных звеньев существует аналогичная связь:
. (2.2.4)
И наоборот
Зная переходную и функцию веса, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:
; (2.2.5)
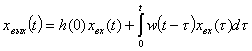, (2.2.6)
где 
, 
– значения 
и при t = 0;
Выражения (2.2.5) и (2.2.6) легко получаются друг из друга, являясь вариантами интеграла Дюамеля или интеграла свертки.
У реальных инерционных звеньев и систем h (0) = 0, так как реакция на их выходе всегда отстает от входного воздействия. Поэтому в дальнейшем выражения (2.2.5) и (2.2.6) приводятся без первого слагаемого.
Временные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразований Лапласа.
Поскольку 
, в случае, когда входное воздействие 
(t) представляет собой единичный импульс 
, и с учетом того, что его изображение по Лапласу 
, получим следующее выражение для изображения функции веса звена:
w(p) =W(p) или 
, т.е.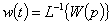 
(2.2.7)
Таким образом, функция веса определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.
В случае, когда (t) = 1(t), учитывая, что L 
= 1/ p, получаем следующее выражение для изображения переходной характеристики:
Следовательно, переходная характеристика звена равна:
2.2.2 Частотные характеристики звеньев и систем
При рассмотрении частотных характеристик считаем, что на входе системы действует гармонический сигнал с амплитудой 
и частотой 
:
. (2.2.8)
По окончании переходного процесса на выходе линейной системы будут существовать гармонические колебания с той же частотой, что и у входного сигнала, но в общем случае отличающиеся от него по амплитуде и фазе, т.е. в установившемся режиме выходная величина звена равна:
, (2.2.9)
где 
– амплитуда установившихся выходных колебаний; 
– фазовый сдвиг между входными и выходными синусоидальными колебаниями.
При изменении частоты изменяется, как соотношение между амплитудами входных и выходных колебаний, так и фазовый сдвиг между ними. При этом зависимость от частоты отношения амплитуд называется амплитудно-частотной характеристикой (АЧХ) (рисунок 2.2.2), т.е.
.
Зависимость величины фазового сдвига от частоты 
называется фазо-частотной характеристикой (ФЧХ).
Определив амплитудно- и фазо-частотную характеристики системы, например, получив их экспериментально, можно построить еще одну частотную характеристику – амплитудно-фазовую (АФЧХ).
Амплитудно-фазовую характеристику, используя 
в качестве полярных координат, строят на комплексной плоскости по следующим правилам. Задаются значением частоты ωi, для которого по графику ФЧХ определяют величину фазового сдвига φ(ωi), а по графику АЧХ – величину A(ωi).
Рисунок 2.2.2 – Примерный вид частотных характеристик инерционной САУ: а) амплитудно-частотная, б) фазово-частотная
Из начала координат комплексной плоскости проводится луч под углом φ(ωi) к положительной действительной полуоси. Угол откладывается против часовой стрелки, если φ(ωi) > 0, т.е. когда выходной гармонический сигнал опережает входной, и в противоположном направлении, если φ(ωi) < 0.Из начала координат по этому лучу откладывается отрезок, длина которого в выбранном масштабе равна A(ωi) (рисунок 2.2.3).
Рисунок 2.2.3 – Примерный вид амплитудно-фазовой частотной характеристики инерционной САУ
Каждая точка амплитудно-фазовой частотной характеристики соответствует определенному значению частоты. Значения для конечного количества точек характеристики наносятся вдоль характеристики и указывают направление возрастания частоты ω.
Очевидно, что возможно и решение обратной задачи:по годографу амплитудно-фазовую частотную характеристику можно построить характеристик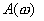и 
и 
. На рисунке 2.2.2 приведен примерный вид этих характеристик для инерционной системы.
Как показано на этих рисунках, у таких звеньев в силу их инерционности амплитудная частотная характеристика по мере увеличения частоты в конце концов спадает до нуля. При этом, чем менее инерционно звено, тем шире его амплитудная частотная характеристика, т.е. тем больше полоса пропускаемых звеном частот, или просто его полоса пропускания.
Теоретически частотная характеристика продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором отношение амплитуд окончательно становится меньше определенного, достаточно малого конечного значения. Это значение обычно берут равным 0,05 (на этой частоте амплитуда выходных колебаний падает до 5 % амплитуды входных колебаний). Наличие максимума у амплитудной частотной характеристики говорит о резонансных свойствах звена.
Частота, соответствующая максимуму амплитудной характеристики, называется резонансной( 
).
Фазовая характеристика у обычных инерционных звеньев (рисунок 2.2.2, б) отрицательна ( (ω)< 0), т.е. выходные колебания отстают по фазе от входных, и это отставание растет с частотой.
Используя символическую форму записи гармонических сигналов xвх(t) и xвых(t), получим аналитические выражения для рассмотренных характеристик, их зависимость между собой и с передаточной функцией системы.
Символическая запись сигналов (2.2.8) и (2.2.9):
, 
.
Определим амплитудно-фазовую характеристику системы, как отношение выходного сигнала системы к входному, выраженное в комплексной форме:
. (2.2.10)
Из выражения (3.2.10) следует, что амплитудно-частотная и фазо-частотная характеристики является соответственно модулем и фазой (аргументом) амплидудно-фазовой характеристики:
A(ω) = |W(jω)| и φ(ω) = argW(jω). (2.2.11)
Очевидно, что на приведенных зависимостях между характеристиками основывалась рассмотренная методика построении W(jω) по A(ω) и φ(ω).
Комплексное выражение для W(jω) может быть представлено, как в форме (2.2.10), так и в виде:
W(jω) = P(ω) + jQ(ω), (2.2.12)
где P(ω), Q(ω) – соответственно вещественная и мнимая частотные характеристики системы.
Таким образом, получаем всего пять частотных характеристик: амплитудно-фазовую W(jω), амплитудно-частотную A(ω), фазо-частотную φ(ω), вещественную частотную P(ω) и мнимую частотную Q(ω). Между этими характеристиками, кроме зависимостей (3.2.11) – (3.2.12), имеются следующие очевидные связи:
; (2.2.13)
(2.2.14)
. (2.2.15)
Частотные характеристики системы не зависят от времени. В этом их принципиальное отличие от временных характеристик. Если временные характеристики определяют поведение системы в переходном процессе при различных типовых входных воздействиях, то частотные выражают зависимость параметров установившихся выходных синусоидальных колебаний от тех же параметров входных колебаний при различных частотах.
Частотные характеристики широко используются в инженерной практике при анализе и синтезе САУ. Особым их достоинством является то, что они могут быть получены экспериментальным путем, что особенно важно для систем, аналитические уравнения которых не представляется возможным получить из-за их сложности или малоизученности технологического процесса.
Несмотря на то, что частотные характеристики, например W(jω), отображают только установившиеся процессы в системе, они в полной мере определяет и ее динамические свойства.
Подставляя производные сигналов 
(t) и 
равные
…. 
…. 
,
в дифференциальное уравнение
получим:
= [ 
] 
.
Из полученного выражения определяем АФХ системы:
. (2.2.16)
Выражение для АФЧХ W(jω) системы может быть получено по ее передаточной функции W (p), в которой достаточно переменную p заменить на jω:
W(jω) = 
. (2.2.17)
Если в выражении 
осуществить аналогичную замену p на jω, получим:
, (2.2.18)
где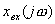 
и 
– изображения Фурье входного и выходного сигналов.
На основании выражения (2.2.18) амплитудно-фазовую частотную характеристику 
можно определить как отношение изображений Фурье выходного и входного сигналов системы при нулевых начальных условиях:
.
Выражению (2.2.5), связывающему с помощью преобразования Лапласа передаточную функцию системы с ее временной характеристикой – функцией веса , соответствуют следующие зависимости для амплитудно-фазовой частотной характеристики:
(2.2.19)
и
(2.2.20)
Первое выражение определяет амплитудно-фазовую частотную характеристику, характеристики системы по его весовой функции, а второе, наоборот, – весовую функцию по . По частотным характеристикам САУ можно непосредственно определить ее реакцию не только на импульсное воздействие, но и на входное воздействие любого вида.
Преобразуя выражение (2.2.16), в котором приняты следующие обозначения:
A(jω)= 
;
B(jω) = 
получим:
, (2.2.21)
где индексами 
и 
отмечены действительные (U)и мнимые (V) части соответствующих комплексных величин в числителе и знаменателе.
Преобразуя (3.2.21), окончательно имеем:
,
где:
Для инженерных расчетов особенно широко используются частотные характеристики, построенные в логарифмическом масштабе, в том числе логарифмическая амплитудно-частотная L(ω), связанная с АЧХ системы зависимостью:
L(ω) = 20lg A(ω). (2.2.22)
Смысл приведенного выражения заключается в следующем. Определим усиление системой мощности сигнала, в виде отношения мощности на выходе Рвых к мощности на входе Рвх. Этот показатель, для удобства оцениваемый в логарифмическом масштабе, с учетом того, что мощность сигнала пропорциональна квадрату его амплитуды, записывается в виде:
.
В качестве единицы усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство принят Бел (по имени американского изобретателя А. Белла). Но поскольку 1 Бел является слишком крупной единицей (ей соответствует изменение мощности в десять раз), в теории автоматического регулирования за единицу измерения принят децибел 1 дБ = 0,1 Б.
С учетом этого можно записать:
,
где величина L(ω) выражена в децибелах.
Используемая совместно с L(ω) фазо-частотная характеристика 
строится в полулогарифмическом масштабе: по оси ординат откладывается значение фазы в градусах или радианах, а по оси абсцисс – 
. При этом единицей измерения частоты является декада. Декадойназывается частотный интервал, граничные значения которого соотносятся в десять раз. В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную единице.
При решении практических задач на оси абсцисс указываются не значения lg ω, а, что более удобно, значения самой частоты ω. Очевидно, что при использовании логарифмического масштаба точка на оси абсцисс, соответствующая ω = 0, находится слева в бесконечности, т.е. логарифмические характеристики строятся не от нулевой частоты, а от некоторого значения, которое определяется данными конкретной задачи.
В дальнейшем для краткости будем в названии различных частотных характеристик опускать слово «частотная», говоря просто о логарифмической амплитудной характеристике L(ω) (ЛАХ), амплитудно-фазовой характеристике W(jω) (АФХ) и т.п.
Для типовых звеньев динамические характеристики представлены в приложении А.
2.3 Краткое описание системы Mathcad
Пакет программ Mathcad фирмы MathSoft относится к программным системам компьютерной математики. Он имеет простой и удобный интерфейс, сочетающийся с мощными средствами для выполнения сложных математических расчетов. Широко используются версии Mathcad 8, Mathcad 10 и Mathcad 2014. Несмотря на различные требования к аппаратным ресурсам, они имеют схожий интерфейс и обеспечивают одинаковый базисный набор математических вычислений. Запуск системы производится следующими способами:
- выполнив клик мышью по ярлыку Mathcad на Рабочем столе Windows;
- нажав кнопку “Пуск” и выбрав Стартового меню Windows раздел “ Программы”/”MachSoft Apps/Mathcad 7 (8 или 2014).
Основное окно пакета, которое для версии 7.0 имеет вид (рисунок 2.3.1):
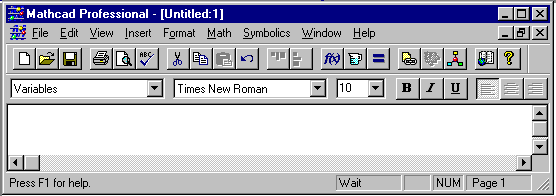
Рисунок 2.3.1 – Основное окно пакета Mathcad
Вверху окна располагается заголовок с именем документа. Ниже располагается строка Главного меню. За ним расположена панель кнопок инструментов, которые дублируют наиболее важные команды Главного меню. Набор кнопок на экране определяется с помощью соответствующих опций раздела View меню. Обычно используются две панели кнопок: панель инструментов (дублирующая ряд наиболее распространенных команд и операций) и панель форматирования (четвертая строка) для выбора типа и размера шрифтов и способа выравнивания текстовых комментариев. Над рабочей областью документа может располагаться строка кнопок вызовов экранных панелей, которые ускоряют работу по вводу операторов, функций, греческих символов, а также вызывают встроенный калькулятор. Далее находится рабочая область документа, в которой вводят математические выражения на языке Mathcad и текстовые комментарии. В низу окна находится строка статуса системы.
Документы системы Mathcad являются файлами с расширением.mcd.
Состав Главного меню Mathcad включает разделы:
- File (Файл) — работа с файлами, Internet и электронной почтой;
- Edit (Правка) — редактирование документов;
- View (Обзор) — настройка интерфейса и средств обзора;
- Insert (Вставка) — установка вставок объектов, шаблонов, графиков;
- Format (Формат) — изменение формата различных объектов;
- Math (Математика) — управление процессом вычислений;
- Graphics (Графика) — работа с графическим редактором;
- Symbolic (Символика) — выбор операций символьного процессора;
- Window (Окно) — управление окнами документов системы;
- Books (Книги) — работа с электронными книгами;
- Help (Помощь) — работа со справочной системой Mathcad.
2.3.1 Формирование документов Mathcad
Электронные документы Mathcad могут включать следующие элементы:
1) математические выражения (Math Region), которые формируются на входном языке и описывают расчетную часть с помощью редактора формул;
2) текстовую часть (Text Region) с пояснениями и комментариями, формируемую встроенным текстовым редактором;
3) визуальные графические зависимости между переменными редактируются встроенным графическим редактором;
4) прочие OLE объекты Windows (рисунки, электронные таблицы и др.).
При работе в документе Mathcad курсор принимает одну из трех форм:
1) красный крестообразный визир (+) служит для указания места для новых блоков на свободном месте документа;
2) красная вертикальная черта маркера ввода (|) служит для обозначения текущей позиции редактирования в текстовом блоке;
3) курсор в виде синих уголков разного размера (ë или û) используется в математических блоках для указания места вставки или удаления отдельных символов, выделяющих части выражения или выражение целиком. Вид курсора зависит от направления ввода. Нажатие клавиши Ins (или клавиш и ® перемещения курсора) меняет направление ввода.
При начале ввода информации с клавиатуры система по умолчанию автоматически пытается интерпретировать как математическое выражение, создавая новое математическое выражение. Однако если синтаксис выражения не соответствует входному языку Mathcad, тогда оно преобразует введенные данные в текстовую область. Математические выражения должны располагаться сверху вниз или слева направо в соответствии с алгоритмом выполняемого расчета.
Для записи текстовой информации в определенном месте mcd-документа необходимо сначала создать Text Region, введя символ кавычек (“). При этом черным прямоугольником обозначатся границы текстовой области, внутри которой вводится текст, поясняющий используемые математические выражения.
Конструирование математических выражений упрощается выделением отдельных фрагментов формул. Выделенная уголком курсора (ë или û) область является операндом для следующего вводимого оператора. Некоторые операторы (возведения в степень, извлечения корня и деления) являются "цепкими": после их ввода все, что набирается следом, считается их операндом (показателем степени, подкоренным выражением или знаменателем). Для отмены ввода операнда нужно нажать клавишу Space.
Ниже приводятся комбинации клавиш редактирования mcd-документов:
- Shift + F5 – замена одной подстроки на другую;
- Enter или Ctrl + F9 – вставка пустой строки;
- Backspace или Ctrl + FlO – удаление пустой строки;
- Alt + Bksp – отмена последней операции редактирования;
- Ctrl + Ins – копирование (Copy) выделенного объекта в буфер обмена;
- Shift + Del – перенос (Cut) выделенного объекта в буфер обмена;
- Shift + Ins – копирование объекта из буфера обмена в окно;
- Ins – включение режима вставки (Insert).
Клавиши управления документами и окнами:
- Ctrl + F4 – закрытие документа;
- Ctrl + F6 – активизация следующего окна;
- Ctrl +P – печать активного документа;
- Alt + F4 – завершение работы с системой (команда Quit);
- F1 – открытие окна помощи (Help);
- F3 – удаление отмеченного объекта с переносом в буфер обмена;
- F4 – вывод объекта из буфера обмена в текущее окно;
- F5 – вызов окна загрузки файлов документов;
- F6 – запись файла текущего документа на диск;
- F7 – подготовка к созданию нового документа;
- F9 – запуск вычислений.
Клавиши (символы) для создания различных объектов документа:
- @ – создание шаблона двумерной графики (2D-графики);
- Ctrl + ® – создание шаблона трехмерной графики (ЗD- графики);
- Ctrl + G – замена символа латинской буквы на греческую;
- Ctrl + M – задание шаблона вектора или матрицы;
- Ctrl + Shift + P – ввод греческой буквы p;
- Ctrl + Z – ввод математического символа бесконечности.
Задание в формулах значений переменных выполняется с помощью оператора присваивания (:=), для ввода которого достаточно нажать клавишу “:”.
Отображение результатов расчета производится с помощью символа равенства (=), в левой части которого записывается имя переменной или выражение.
2.3.2 Определение корней характеристического уравнения системы
Выражение передаточной функции САР удобно представить как отношения полиномов числителя и знаменателя:
, (2.3.1)
где a3, …, a0 – коэффициенты полинома числителя;
b3, …, b0 – коэффициенты полинома знаменателя.
Для определения нулей передаточной функции необходимо с помощью Mathcad решить уравнение, полученное из полинома числителя вида
a3×p3+a2×p2+a1×p+a0=0. (2.3.2)
Полюса получают из характеристического уравнения системы
b4×p4+b3×p3+b2×p2+b1×p+b0=0. (2.3.3)
В Mathcad для определения корней уравнений (2.3.2) и (2.3.3) задаются вектора коэффициентов полиномов числителя и знаменателя. При задании векторов матрицей следует следить, чтобы номер индекса вектора соответствовал степени при операторе Лапласа. Номер индекса вводится с помощью символа “[“.
Корни алгебраического уравнения определяются Mathcad с помощью функции polyroots(<вектор>), аргументом которой является вектор (матрица-столбец) коэффициентов полиномов уравнения.
Пример определения корней для полиномов передаточной функции вида
. (2.3.4)
Получены корни полинома числителя: p1=–10, p2=–2,213×10-8+10i, p3=–10i.
Получены корни: p1=–97,698, p2= –2,08, p3,4= –0,111±4,959i
Здесь использовалось два способа задания исходных значений полиномов: поэлементно (для a) и вектором (для b). При определении элемента вектора сначала набирается имя переменной вектора, а затем нажимается клавиша «[» и вводится индекс элемента вектора. Для ввода значений вектора следует нажать Ctrl+M и в раскрывшемся диалоговом окне указать в поле Rows порядок полинома, а в Columns – ввести 1. В шаблоне вектора на месте черных точек вводятся значения элементов вектора, начиная с верхней позиции, которая соответствует коэффициенту полинома при р=0.
С помощью переменной i или j (мнимых единиц) в Mathcad обозначаются мнимые части комплексных корней.
3.4 Расчет частотных характеристик системы с помощью Mathcad
Для получения частотных характеристик следует задать ранжированную переменную, определяющую расчетный диапазон частот в формате
<имя переменной частоты>:=<первое значение>,<второе>.. <последнее>.
Здесь диапазон.. вводится при нажатии клавиши “;”.
Далее определяется комплексная переменная p(w):=i×w. Здесь i – мнимая единица, считается известной в Mathcad (возможно задать ее значение i:=). Квадратный корень задается в шаблоне, который вызывается символом “\”. Затем вводится выражение передаточной функции как переменной, зависящей от р.
Пример задания частоты от 0.025 до 100 с шагом 0.025 с-1 для (2.4).
Далее в виде функции с помощью оператора присваивания задаются расчетные выражения полиномов или передаточной функции с использованием определенной переменной р. В левой части оператора в скобках после имени функции, указывается имя ранжированной переменной-аргумента. Например,
Затем определяются выражения различных частотных характеристик. При этом используются следующие встроенные функции Mathcad:
Re (<выражение>) – выделение действительной части выражения;
Im (<выражение>) – выражение мнимой части выражения;
|<выражение>| – взятие модуля выражения;
arg (<выражение>) – взятие аргумента выражения в радианах.
Пример определения выражений частотных характеристик в Mathcad.
Двухмерные графики в декартовой системе координат строятся в Mathcad с помощью шаблона, вызываемого символом @.
 |
максимум Y
Зона графика
переменная Y
минимум Y
минимум X максимум
Рисунок 2.3.2 – Шаблон двухмерного графика 2D XY Plot
При заполнении шаблона сначала указываются переменные (или расчетные выражения), значения которых отображаются в осях X и Y. При этом следует указывать в скобках полную структуру ранжированной переменной. Можно не указывать диапазон