Тема: Понятие правильного многогранника.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава III, § 3, п. 36), решить задачи самостоятельной работы и ответить письменно на вопросы кроссворда.
Теоретический минимум и задачи
«Правильных многогранников вызывающе мало, – написал когда-то Л.Кэрролл, – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».
Определение: Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Существует 5 типов правильных многогранников:
Правильный тетраэдр
| 
Правильный октаэдр
| 
Правильный додекаэдр
| 
Правильный гексаэдр
| 
Правильный икосаэдр
|
Правильный тетраэдр
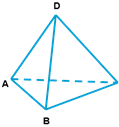В переводе с греческого «тетраэдр» - четырёхгранник. У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра.
Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
Правильный гексаэдр
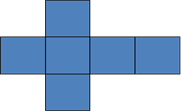
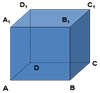Гексаэдр - шестигранник.
У правильного гексаэдра (куба) все грани -квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными рёбрами.
Правильный октаэдр
Октаэдр - восьмигранник.
У октаэдра грани – правильные треугольники, но в отличие от тетраэдра, в каждой вершине сходится по четыре ребра.
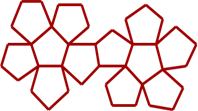
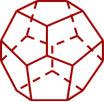Правильный додекаэдр
Додекаэдр - двенадцатигранник.
У додекаэдра грани – правильные пятиугольники.
В каждой вершине сходится по три ребра.
Правильный икосаэдр
Икосаэдр - двадцатигранник.
У икосаэдра грани – правильные треугольники.
В каждой вершине сходится по пять рёбер.
Историческая справка
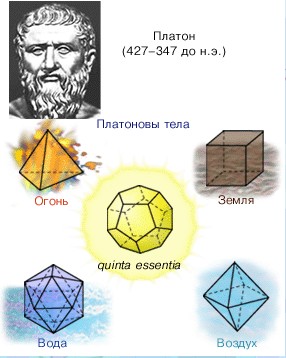О существовании всего лишь пяти правильных многогранников знали еще в Древней Греции. Великий древнегреческий мыслитель Платон считал, что четыре из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа») или «пятая сущность». Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков.
Применение в кристаллографии
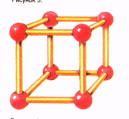Тела Платона нашли широкое применение в кристаллографии, так как многие кристаллы имеют форму правильных многогранников. Например, куб - монокристалл поваренной соли (NaCl), октаэдр - монокристалл алюмокалиевых квасцов, одна из форм кристаллов алмаза – октаэдр Скелет одноклеточного организма феодарии представляет собой икосаэдр.Молекулы воды имеют форму тетраэдра.Кристаллы пирита имеют форму додекаэдра.Минерал куприт образует кристаллы в форме октаэдров.
Правильные многогранники издавна нашли применение в искусстве, архитектуре и многих других сферах человеческой деятельности.
Самостоятельная работа
Решить задачи № 1-2, используя план решения
Задача №1. Найдите высоту правильного тетраэдра с ребром 10 см.
Дано: ABCД – правильный тетраэдр, AВ = 10 см
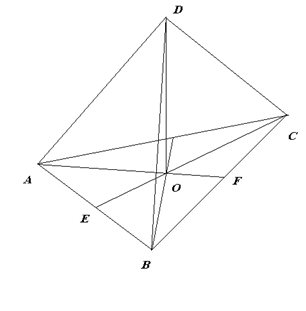Найти: высоту тетраэдра
Решение.
1) AF – медиана ΔABС, значит ВF = ______
2) Из ΔABF по теореме _______ найдем АF
AF2 = AB2 – BF2: AF=________
3) О делит отрезок AF в отношении 2:1, поэтому АО = _____________________
4) Из ΔADO по теореме Пифагора найдем DO
DO2 = ____________; DO = ____________
Ответ: ______см
Задача №2.
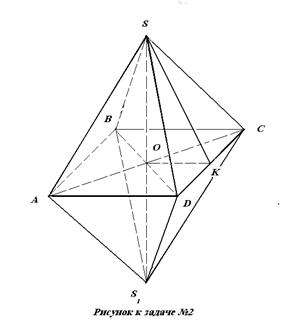
Кристалл имеет форму октаэдра, состоящего из двух правильных пирамид с общим основанием, ребро основания пирамиды 6 см. Высота октаэдра 14 см. Найдите площадь боковой поверхности кристалла.
Решение.
1) Sбок = 2 Sпир = p ∙ SK (где SK – апофема, p – полупериметр ABCD)
2) Находим ОК _________________________
3) Находим SO ________________________
4) Находим SK ________________________
5) Вычисляем Sбок ______________________
Ответ:
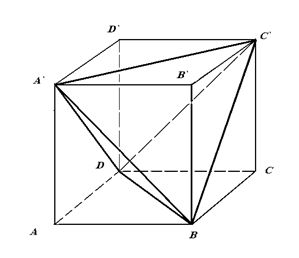
№3. Докажите, что концы двух непараллельных диагоналей противолежащих граней куба являются вершинами тетраэдра.
| Кроссворд «Многогранники» | |||||||||||||||||||||
| 1 | |||||||||||||||||||||
| 2 | 3 | ||||||||||||||||||||
| 4 | |||||||||||||||||||||
| 5 | 6 | ||||||||||||||||||||
| 7 | |||||||||||||||||||||
| 8 | |||||||||||||||||||||
| 9 | 10 | ||||||||||||||||||||
| 11 | |||||||||||||||||||||
| 12 | |||||||||||||||||||||
По горизонтали:
2. Правильный шестигранник. 4. Плоские многоугольники, из которых состоит поверхность многогранника. 5. Высота боковой грани правильной пирамиды. 7. Правильный двадцатигранник. 8. Правильный двенадцатигранник. 10. Основание правильной четырёхугольной пирамиды. 11. Древнегреческий философ, подробно описавший правильные многогранники. 12. Призма, основанием которой служит параллелограмм.
По вертикали:
1. Треугольная пирамида. 3. Сторона грани многогранника. 6. Тело, поверхность которого состоит из конечного числа плоских многоугольников. 9. Автор теоремы (формулы) В+Г=Р+2, показывающей зависимость между вершинами, гранями и рёбрами выпуклого многогранника.