Основным и наиболее известным, понятным считается временн о е представление сигналов, т. е. зависимость изменения значения сигнала от времени.
Существует другое представление тех же сигналов — спектральное.
Рассмотрим простейший периодический непрерывный сигнал – гармоническое колебание
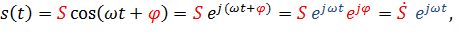 (1.1)
(1.1)
где S, ω и φ — амплитуда, угловая частота и начальная фаза колебания,
 – комплексная амплитуда.
– комплексная амплитуда.
Пусть для упрощения рассуждений начальная фаза φ = – π/2, а частота ω1:
s(t) = S cos(ω1 t – π/2) = S sin(ω1 t). (1.2)
Колебание (1.2) заданной частоты, амплитуды и начальной фазы можно представить в виде двух графиков, независимой переменной в которых будет угловая частота: на одном из них на частоте ω1 изобразить линию высотой, равной амплитуде сигнала S, на другом – линию, равную по величине значению фазы φ = – π/2.
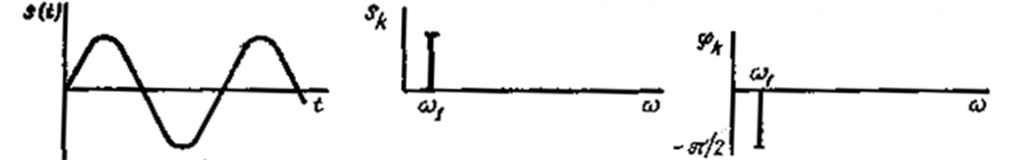
Если рассмотреть сигнал s(t), состоящий из суммы двух гармонических колебаний, например первой и третьей гармоник
 , (1.3)
, (1.3)
то возможно его представление в форме рис. 1.5,г, где отложены амплитуды и фазы этих гармоник

А если рассмотреть сигнал s(t), состоящий из суммы трех гармонических колебаний: первой, третьей и пятой гармоник
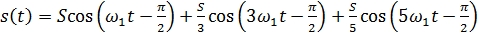 (1.4)
(1.4)
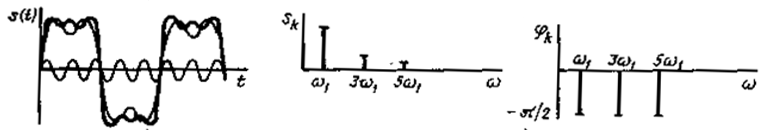
Диаграммы распределения амплитуд и фаз гармонических колебаний по частоте называются спектральными диаграммами сигнала, а линии, соответствующие амплитудам и фазам гармоник, — спектральными линиями. Закон распределения амплитуд Sk составляющих периодического сигнала по частоте называется спектром амплитуд этого сигнала, а закон распределения фаз φk — спектром фаз.
Если нас интересуют не значения амплитуд и начальных фаз гармоник, входящих в состав сложного колебания, а только частоты, то говорят о спектре частот сигнала.
Продолжаем.
Суммируя бесконечное количество нечетных гармоник
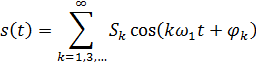
| (1.5) |
где Sk=S/k, φk = – π/2, а индекс k принимает нечетные значения, получаем сигнал в форме последовательности прямоугольных импульсов с амплитудой πS/4.
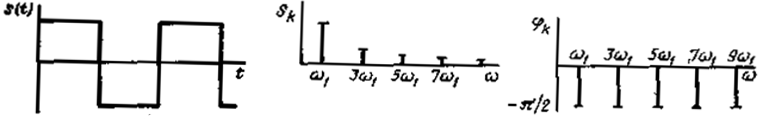
Или в общем виде
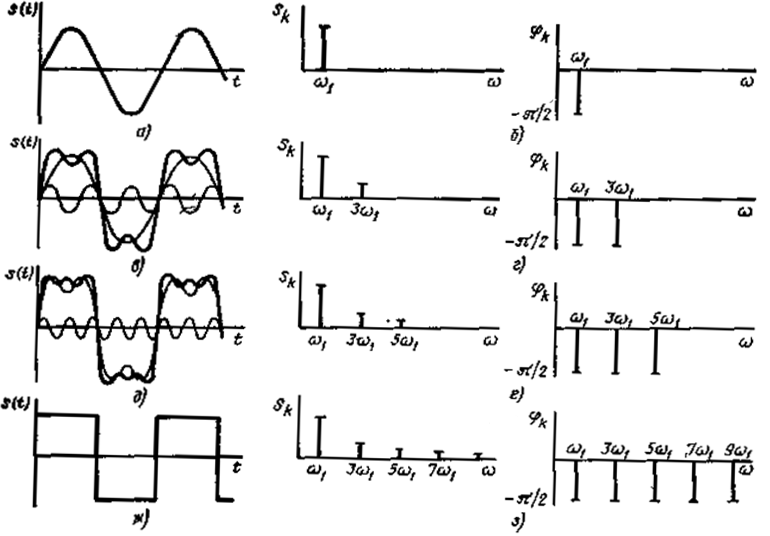
Рис. 1.1. Временное и спектральное представление сигналов: синусоидального (а и б), суммы первой и третьей гармоник (в и г), суммы первой, третьей и пятой гармоник (д и е), последовательности прямоугольных импульсов (ж и з)
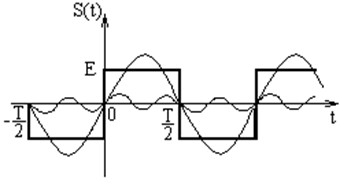
Обратить внимание: амплитуда импульсов меньше амплитуды первой гармоники, 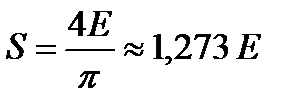 .
.
Периодический сигнал любой формы может быть представлен в виде суммы (в общем случае бесконечной) гармонических колебаний – тригонометрический ряд, ряд Фурье.
В эту сумму могут входить как четные, так и нечетные гармоники, а амплитуды Sk а начальные фазы φk принимают конкретные значения в зависимости от формы сигнала:
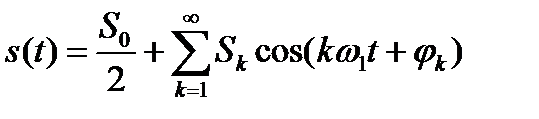 (1.6)
(1.6)
Значения Sk и φk – комплексную амплитуду  k–той гармоники (включая S0) вычисляются по формуле
k–той гармоники (включая S0) вычисляются по формуле
 (1.7)
(1.7)
где Т – период колебаний, а 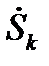 – комплексная амплитуда.
– комплексная амплитуда.
Для постоянной составляющей S0 /2: k = 0
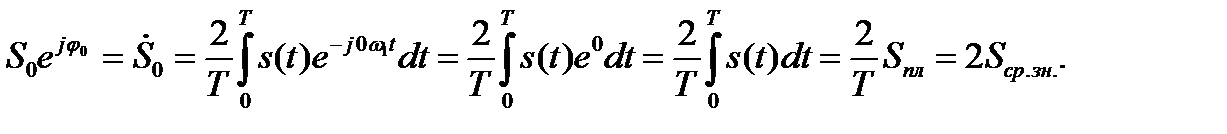
Периодический сигнал может быть представлен суммой гармонических колебаний с начальными фазами, равными нулю: " k φk = 0
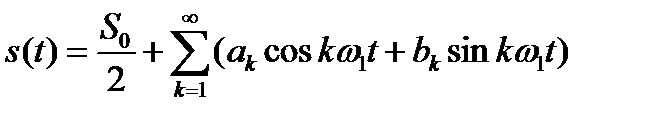 . (1.8)
. (1.8)
Тогда
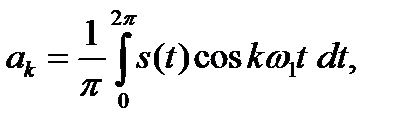
 (1.9)
(1.9)
Обратно: из (1.6), (1.7) и (1.1) получим
 . (1.10)
. (1.10)
Выражения (1.7) и (1.10) называют парой преобразований Фурье.
Первое позволяет по зависимости s (t) рассчитать спектральные составляющие сигнала, а второе по спектральным составляющим – восстановить сигнал s (t).
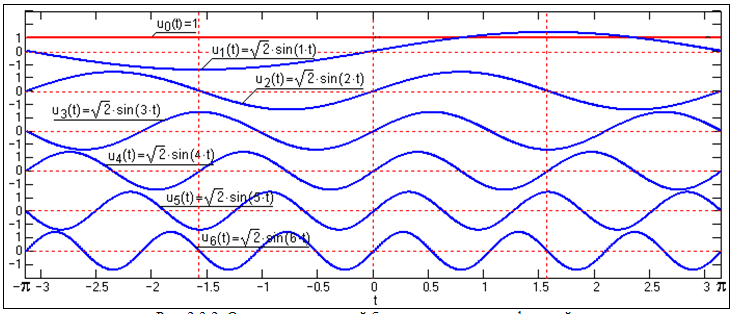
Пример: ортонормированный базис гармонических функций
Пример 2:
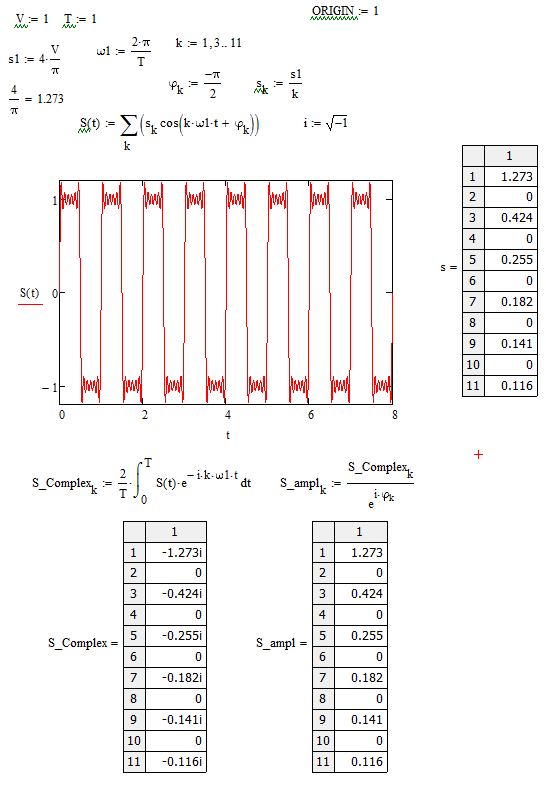
Пример 3:
