Расчет геометрических и электродинамических характеристик облучателей.

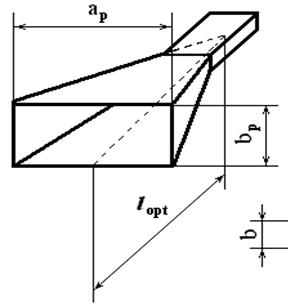
Рупор пирамидальный

Расчет сводится к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва, и диаграммы направленности облучателя.

Диаграммы направленности рупорной антенны рассчитываются по формулам:

В плоскости H

В плоскости E

где ,

Ширина луча оптимального пирамидального рупора на уровне 0.5 по мощности (рад) определяется по формулам:

В плоскости H

В плоскости E

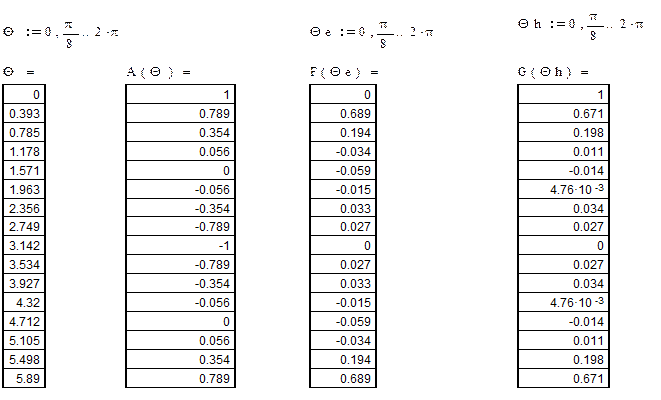
где значения определяются по аппроксимированной диаграмме направленности . Для этого построим ее в прямоугольной системе координат (рисунок 5).

Рисунок 5 – Аппроксимированная нормированная ДН облучателя

Найдем поперечные размеры рупора:

,

Построим ДН рупорной антенны в плоскости E и в плоскости H (рисунок 7).

Аппроксимированная функция: где n = 6.

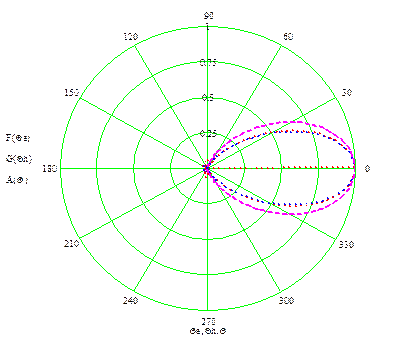
Рисунок 7 - ДН рупорной антенны в плоскости E и Н

Для оптимального рупора (наибольший КНД) продольные и поперечные размеры связаны между собой соотношениями:

в плоскости E

в плоскости H

где - длины рупора в соответствующих плоскостях.

Распределение поля в апертуре зеркала

Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам.

где - диаграмма направленности облучателя,

- угол раскрыва,

φ- текущий угол.

Распределение поля в апертуре зеркала в плоскости E:

Распределение поля в апертуре зеркала в плоскости H:

Таблица 3

φ, град	ρ			φ, град	ρ
0.01	0.0034			0.43	0.15	0.677	0.623
0.03	0.01	0.998	0.998	0.45	0.158	0.652	0.596
0.05	0.017	0.995	0.994	0.47	0.165	0.627	0.569
0.07	0.24	0.99	0.987	0.49	0.172	0.602	0.542
0.09	0.031	0.983	0.979	0.51	0.179	0.577	0.515
0.11	0.038	0.975	0.969	0.53	0.187	0.552	0.488
0.13	0.045	0.965	0.957	0.55	0.194	0.527	0.462
0.15	0.052	0.954	0.944	0.57	0.202	0.503	0.437
0.17	0.059	0.941	0.928	0.59	0.209	0.479	0.412
0.19	0.066	0.927	0.911	0.61	0.217	0.455	0.388
0.21	0.073	0.911	0.893	0.63	0.224	0.431	0.364
0.23	0.08	0.894	0.873	0.65	0.232	0.408	0.341
0.25	0.086	0.876	0.852	0.67	0.24	0.386	0.319
0.27	0.093	0.857	0.829	0.69	0.247	0.364	0.298
0.29	0.101	0.837	0.806	0.71	0.255	0.343	0.278
0.31	0.108	0.816	0.782	0.73	0.263	0.322	0.258
0.33	0.115	0.795	0.756	0.75	0.271	0.302	0.24
0.35	0.122	0.772	0.731	0.77	0.279	0.283	0.222
0.37	0.129	0.749	0.704	0.79	0.287	0.264	0.205
0.39	0.136	0.725	0.677	0.81	0.295	0.246	0.189
0.41	0.143	0.701	0.65

На рисунке 8 представлен график распределения поля в апертуре зеркала.

Рисунок 8 – Распределение поля в апертуре зеркала

Расчет пространственной диаграммы направленности и определение параметров параболической антенны.

Инженерный расчёт пространственной ДН параболической антенны часто сводится к определению ДН идеально круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:

где J₁ и J₂ – цилиндрические функции Бесселя первого и второго порядка;

k₁=Е_кр/Е_max=cos(φ₀/2)F_обл(φ₀) – коэффициент, показывающий во сколько раз амплитуда возбуждающего поля, на краю раскрыва меньше амплитуды в центре раскрыва, в соответствующей плоскости с учётом различий расстояний от облучателя до центра и края зеркала.

Нормированная ДН зеркальной параболической антенны в плоскости E (рисунок 9):

Рисунок 9 - Нормированная ДН зеркальной параболической антенны в плоскости E

Нормированная ДН зеркальной параболической антенны в плоскости H (рисунок 10):

Рисунок 10 - Нормированная ДН зеркальной параболической антенны в плоскости H

По диаграмме направленности параболической антенны определим уровень боковых лепестков: УБЛ = -20log(E₀/E₁) = 18 дБ