Если множества X и Y совпадают, X = Y, то говорят не о соответствии, а об отношении между элементами множества X.
Бинарные соответствия между X и X называют бинарными отношениями на множестве X.
Например, если X – множество людей, то соответствия «Человек х – друг человека у», «х живет в одном доме с у», «Человек х – отец человека у» являются отношениями между людьми.
Отношение на множестве X задано, если указано множество Г, являющееся подмножеством декартова произведения Х×Х.
Отношения, как и соответствия, принято обозначать буквами R, S, T, Q и др. и писать xRy, xSy и т. д.
Множество X называют областью задания отношения R, а множество Г – графиком отношения R.
Рассмотрим, например, на множестве Х={1; 2; 3; 4} отношение «х>у». График этого отношения – множество Г={(2; 1); (3; 1); (3; 2); (4; 1); (4; 2); (4; 3)}, состоящее из всех тех пар (х; у), х?Х, у?Х, для которых х>у.
Способы задания отношения:
1. Перечисление упорядочных пар или графиком Г,
2. Словесным описанием,
3. Ориентированным графом,
4. Графиком в ПДСК (только для числовых множеств),
5. Таблицей (например, график дежурства – задает соответствие между учениками и днями недели),
6. Аналитически или формулой (например, у=х+5).
Чтобы наглядно представить отношение R в множестве X, изобразим точками элементы этого множества, а затем проведем стрелки от х к у для всех пар точек (х; у) таких, что xRy. Полученный чертеж называют графом отношения R, а точки, изображающие элементы множества X, вершинами графа
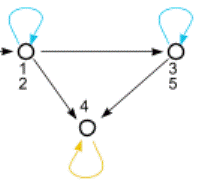
Построим, например, граф отношения R: «х≤у», заданного на множестве
Х= { 1/2; 3/5;4}. Для этого рисуем диаграмму множества X, изобразив элементы этого множества точками. Затем проводим стрелки от х к у для всех пар (x; у) таких, что х меньше или равент у. Получаем граф отношения «х≤у», заданного на множестве Х= {1/2; 3/5;4}.
Каждое из этих чисел равно самому себе, поэтому для каждой точки х, изображающей элемент множества X, рисуем стрелку, начало и конец которой совпадают с х. Стрелку на графе, у которой начало и конец совпадают, называют петлей. Следовательно, граф отношения R в каждой вершине имеет петли.
Свойства отношений
Пусть на множестве X задано некоторое отношение R
1. Отношение R называется рефлексивным, если для любого х из множества X истинно xRx. Другими словами, отношение R на множестве X рефлексивно, если каждый элемент х £ X находится в отношении R с самим собой.
 Так, рефлексивно отношение конгруэнтности на множестве геометрических фигур, поскольку каждая фигура конгруэнтна самой себе.
Так, рефлексивно отношение конгруэнтности на множестве геометрических фигур, поскольку каждая фигура конгруэнтна самой себе.
2. Отношение R называется антирефлексивным, если ни один элемент х из множества X не находится в отношении R с самим собой.
Например, отношение «Прямая х перпендикулярна прямой у» на множестве прямых плоскости антирефлексивно, так как ни одна прямая не перпендикулярна самой себе.
Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «Точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны самим себе, а точки, не лежащие на прямой l, себе не симметричны.
3. Отношение R называется симметричным, если для любых элементов х и у из множества X из xRy следует yRx.
Так, симметрично отношение параллельности на множестве прямых плоскости: если прямая х параллельна прямой у, то и прямая у параллельна прямой х.
4. Отношение R называется асимметричным если ни для каких элементов х и у из множества X не может случиться, что одновременно и xRy, и yRx.
Примером асимметричного отношения является отношение <y», заданное на множестве действительных чисел, так как ни про какую пару чисел х и у нельзя сказать, что одновременно и х<у, и у<х.
5. Отношение R антисимметрично, если xRy и yRx одновременно выполняются в том и только в том случае, когда х=у. Антисимметричное отношение – объединение асимметричного отношения с отношением тождества.
6. Отношение R называется транзитивным, если для любых элементов х, у и z из множества X из того, что xRy и yRz, следует, что xRz.
Например, транзитивно отношение «Отрезок х длиннее отрезка у» в множестве отрезков: если отрезок х длиннее отрезка у и отрезок у длиннее отрезка z, то отрезок х длиннее отрезка г.
Свойства рефлексивности, симметричности и транзитивности наглядно иллюстрируются при изображении отношений графами. Если отношение R в множестве X рефлексивно, то граф этого отношения в каждой вершине имеет петлю.
Если отношение R симметрично, то граф вместе с каждой стрелкой, идущей из точки х в точку у, должен содержать стрелку, соединяющую те же точки, но идущую в обратном направлении.
Граф транзитивного отношения вместе со стрелками, идущими от х к у и от у к z, должен содержать и стрелку, идущую от х к z.
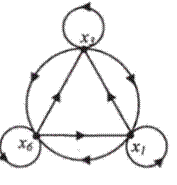
Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы (классификацией).
Множество X всех студентов пединститута можно разбить на подмножества, состоящие из студентов, обучающихся на одном и том же курсе. Если обучение длится четыре года, то получаем четыре подмножества: студентов первого курса, студентов второго курса, студентов третьего курса и студентов четвертого курса. Никакие два из этих множеств не имеют общих элементов (студент не может сразу учиться и на втором, и на третьем курсе), а объединением этих множеств является множество X всех студентов. Говорят, что X разбито на четыре попарно непересекающихся подмножества Х1 Х2, Х3, Х4. То же множество X можно разбить на непересекающиеся подмножества и другими способами, например, на юношей и девушек, по возрасту, на комсомольцев и не комсомольцев и т. д.
Вообще, можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:
1. Все подмножества, образующие разбиение, непусты.
2. Любые два таких подмножества не пересекаются.
3. Объединение всех подмножеств есть данное множество.
Так, множество натуральных чисел можно разбить на три подмножества – множество простых чисел, множество составных чисел и множество, состоящее из единицы. Это же множество можно разбить и на два класса – класс четных и класс нечетных натуральных чисел.
Разбиение множества на попарно-непересекающиеся подмножества лежит в основе всевозможных классификаций. Понятие «класс» и его синонимы «тип», «семейство», «род», «вид», «сорт» широко применяются во всех областях человеческой деятельности. Так, в биологии все живые организмы распределяют на типы, в сельском хозяйстве сортируют по размеру или весу фрукты, слова в словарях разбивают на подмножества, располагая их в алфавитном порядке, и т. д.
Разбиение множества на попарно-непересекающиеся подмножества часто производят по некоторому свойству, которое может принимать различные значения. Например, можно производить разбиение на классы по цвету, объединяя в один класс предметы одного и того же цвета. При этом красные предметы попадут в один класс зеленые – в другой, черные – в третий и т. д. Можно сказать, что разбиение производится на основе отношения «х имеет тот же цвет, что и у». Точно так же разбиение студентов по курсам производится на основе отношения «х учится на том же курсе, что и у».
Но не всякое отношение R между элементами множества дает возможность разбить это множество на классы. Нельзя, например, разбить на попарно-непересекающиеся подмножества множество студентов некоторого института при помощи отношения «Студент х знаком со студентом у». Действительно, если х знаком с у, то х и у окажутся в одном подмножестве. Если у знаком с г, то z должен находиться в одном подмножестве с у и, следовательно, с х. Но может случиться, что х не знаком с z. Тогда окажется, что в одном подмножестве есть люди, которые друг с другом не знакомы, а этого не должно быть при разбиении множества по указанному отношению.
С другой стороны, такие отношения, как «быть однокурсником» в множестве студентов некоторого института, «родиться в одном и том же году» в множестве людей, «иметь один и тот же остаток при делении на данное число» в множестве натуральных чисел, дают возможность разбить множество, в котором они рассматриваются, на классы. Далее мы рассмотрим, какими должны быть свойства отношения, чтобы с его помощью можно было разбить множество на классы.
Если отношение R в множестве X обладает свойствами рефлексивности, симметричности и транзитивности, то его называют отношением эквивалентности.
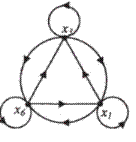
Выше представлен граф отношения эквивалентности.
Примерами отношений эквивалентности являются отношения, рассмотренные нами раньше: «быть однокурсником» (на множестве студентов некоторого института), «иметь один и тот же корень» (на множестве слов) и др.
С каждым таким отношением связано разбиение множества на непересекающиеся подмножества. И это не случайно. Имеет место следующая теорема Для того чтобы отношение R позволяло разбить множество X на классы, необходимо и достаточно, чтобы R было отношением эквивалентности.
Рассмотрим несколько примеров отношений эквивалентности.
1. Отношение «Выражения х и у имеют одинаковые числовые значения» на множестве числовых выражений является отношением эквивалентности, поскольку оно
а) рефлексивно: значение выражения х совпадает со значением выражения х;
б) симметрично: если значение выражения х совпадает со значением выражения у, то и значение выражения у совпадает со значением выражения х;
в) транзитивно: если значение выражения х совпадает со значением выражения у, а значение выражения у совпадает со значением выражения z, то значение выражения х совпадает со значением выражения z.
Множество всех числовых выражений разбивается этим отношением на классы, в каждом из которых находятся выражения, значения которых попарно совпадают. Так, выражения 5+3, 23, 2+2+2+2 находятся в одном классе (их значения равны восьми), а выражения 7–3,22, 16: 4 – в другом (их значения равны четырем).
2. Во множестве прямых на плоскости отношение параллельности является отношением эквивалентности. Прямые х и у, лежащие в одной плоскости, параллельны, если они либо не пересекаются, либо совпадают. Поэтому отношение параллельности
а) рефлексивно: х\\х для любой прямой х;
б) симметрично: если х\\у, то у\\х;
в) транзитивно: если х\\у и y\\z, то x\\z.
Отношением параллельности множество всех прямых плоскости разбивается на классы, состоящие из параллельных друг другу прямых. Такие классы называют пучками параллельных прямых.
В начальном курсе математики также встречаются отношения эквивалентности, например отношение «Выражения х и у имеют одинаковые числовые значения» в множестве числовых выражений. Выражения, принадлежащие одному и тому же классу эквивалентности, называют равными.
Отношение порядка
Отношением порядка называют антисимметричное и транзитивное отношение.
Если отношению порядка присуще еще свойство рефлексивности, то порядок нестрогий.
Если ему присуще свойство антирефлексивности, то порядок строгий.
Свойством транзитивности и асимметричности и антирефлексивности обладают многие отношения, например, отношение «больше» на множестве натуральных чисел или отношение «выше» на множестве людей, сравниваемых по росту. Это отношения строгого порядка. Об отношениях «следует за», «больше», «выше» также говорят, что они являются отношениями строгого порядка.
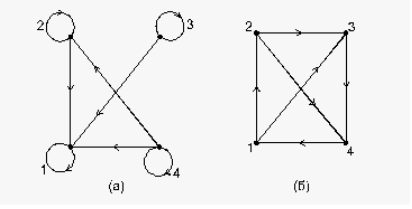
Выясним особенности графа отношения строгого порядка. Отметим, что граф отношения строгого порядка не имеет петель, нет обратных стрелок. Если из х идет стрелка в у, а из у – в z, то из х идет стрелка в z.
Наряду с отношением «х<y» («x>y») в математике рассматривают отношения «х≤y» («х≥у»), представляющие собой объединение отношений «х<y» и «х= у» («х>y» и «х=y»).
Говорят, что «х≤у» является отношением нестрогого порядка.
К нестрогому порядку также принадлежат, например, такие отношения: «не выше» (на множестве людей, сравниваемых по росту); «не больше» (на множестве действительных чисел); «быть делителем» (на множестве натуральных чисел).
Если на множестве рассмотреть отношение нестрогого порядка, то граф этого отношения в каждой вершине будет иметь петли (в остальном он похож на предыдущий граф).
Множество X, на котором задано отношение порядка R (строгого или нестрогого), называется частично упорядоченным множеством. Часто говорят также, что в этом случае множество X упорядочено отношением R.
Примером такого множества является множество натуральных чисел по отношению меньше или больше.