Тема: Сечения пирамиды.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава I, § 4, п. 14), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
Напомним основные положения о сечениях многогранников.
Определение. Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела с плоскостью.
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
a) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
b) параллельные грани плоскость сечения пересекает по параллельным прямым.
Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.
Рассмотрим примеры построения сечений пирамиды.
| M |
| N |
| C |
| D |
| B |
| A |
| S |
Решение:
| C |
| D |
| K |
| M |
| N |
| B |
| A |
| S |
|
|
Пример 2: Построить сечение четырёхугольной пирамиды плоскостью, проходящей через сторону основания и точку на боковом ребре. АВСD – не параллелограмм. Сечение проходит через AB и точку M.
Решение:
Т. к. DC не параллельна AB, то они пересекутся в точке K. Точка K принадлежит секущей плоскости и грани SDC, следовательно MK – линия пересечения грани SDC и секущей плоскости. MK пересечёт SD в точке N. Соединим точки A N B M. Получим искомое сечение. Задача имеет 1 решение.
Пример 3: Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
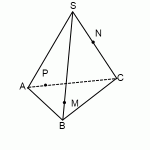Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
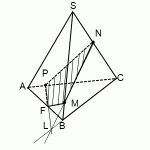Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
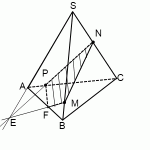Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат в одной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
|
|
Пример 4: 
– правильная треугольная пирамида со стороной основания 
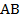равной 
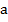и высотой 
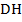равной 
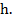Постройте сечение пирамиды плоскостью, проходящей через точки 
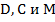, где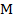 
– середина стороны 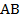, и найдите его площадь
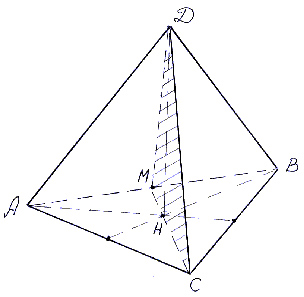Решение.
Сечением пирамиды является треугольник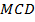 
. Найдем его площадь.
Так как основание пирамиды – равносторонний треугольник и точка 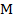– середина стороны, то 
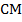является высотой и тогда, 
.
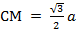Площадь треугольника можно найти:
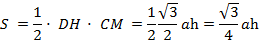
Самостоятельная работа
Задача № 1: Построй те сечение в треугольной пирамиде, все рёбра которой равны 5 см, через сторону основания и середину противоположного ребра. Найдите периметр сечения.
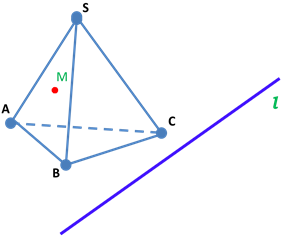
Задача № 2: Точка М принадлежит грани АBS. Прямая l лежит в плоскости основания. Построить сечение, проходящее через след- прямую l.
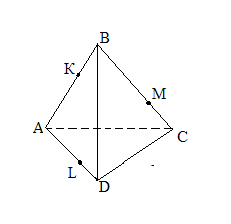
Задача № 3: Построить сечение пирамиды АВСD плоскостью, проходящей через точки К, L, M.
Контрольные вопросы:
1. Что мы называем сечением многогранника?
2. Какие правила нужно соблюдать при построении сечения?
3. На какие фигуры разобьётся пирамида при построении сечения пирамиды плоскостью, параллельной основанию? Какая фигура получится в сечении?
4. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, что вы скажите о линии пересечения плоскостей?