Разложение многочлена на множители.

Показательная функция с комплексным показателем и ее свойства.

 

Пусть , если X и Y-действительные переменные, то Z называется комплексным переменным. Каждому значению комплексного переменного Z на плоскости XOY (плоскости комплексного переменного) соответствует определенная точка.

 

Опр. Если каждому значению комплексного переменного Z из некоторой области комплексных значений соответствует определенное значение другой комплексной величины , то есть функция комплексного переменного Z.

 

вводится понятие предела производной, интеграла и т.д.

Рассмотрим одну функцию комплексного переменного:

показательную функцию.

 

причем определяется так:

Свойства показательной функции:

 

1. Если 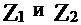– комплексные числа, то:

= и

3. Если m целое, то:

 

4. Справедливо тождество:

5. Рассмотрим комплексную величину: ,

где u(x) и v(x) – действительные функции действительного аргумента.

Тогда называется комплексной функцией действительного пере­менного.

Рассмотрим показательную функцию вида:

ее можно представить в виде: .

Формула Эйлера.

Если в формуле: положить х=0, то получим формулу Эйлера:

при у = -у будем иметь:

Формула Эйлера выражает показательную функцию, через тригонометрические функции. Складывая и вычитая эти равенства, получим:

Получим показательную форму комплексного числа:

Запишем комплексное число в тригонометрической форме . Применим формулу Эйлера . - показательная форма комплексного числа.

Теорема Безу

Определение. Функция , где n - целое число называется многочленом (полиномом) или целой рациональной функцией числа х. Здесь n – степень многочлена. Корнем многочлена называется такое значение х при котором многочлен обращается в нуль. Здесь коэффициенты могут быть действительными или комплексными числами, а переменная х также может принимать действительные или комплексные значения.

Теорема 1. (Теорема Безу) При делении многочлена на разность получается остаток равный .

Доказательство. При делении на частным будет многочлен степень которого на единицу ниже степени , остатком будет постоянное число т. е.

. (1)

Это равенство справедливо для всех . Пусть . Тогда предел левой части , а правой,

Так как функции и равны между собой, то равны и их пределы: .

Следствие. Если а есть корень многочлена, т. е. , то делится без остатка на т.е. .

Пример: Показать, что многочлен делится без остатка на .

Решение:

Разложение многочлена на множители.

Рассмотрим уравнение с одним неизвестным.

Определение. Всякое число (действительное или комплексное) которое, будучи подставлено в уравнение вместо х, обращает уравнение в тождество, называется корнем уравнения.

Пример. Найти корни уравнения . Решение: уравнение с одним неизвестным. Корнями являются числа:

; ;

Определение. Если уравнение имеет вид , где - многочлен степени n, то уравнение называется алгебраическим уравнением степени n. Из определения следует, что корни алгебраического уравнения те же, что и многочлена .

Возникает вопрос – всякое ли уравнение имеет корни?

В случае если уравнение не алгебраическое, то оно может не иметь ни одного корня, ни действительного, ни комплексного, например: .

Но в случае алгебраического уравнения ответ дает основная теорема алгебры.

Теорема 2. (Основная теорема алгебры) Всякая целая рациональная функция имеет, по крайней мере, один корень действительный или комплексный.

Доказательство в курсе высшей алгебры, но пользуясь этой теоремой можно доказать следующую теорему:

Теорема 3. Всякий многочлен n –й степени разлагается на n линейных множителей вида и множитель равный коэффициенту при .

Доказательство: Пусть - многочлен степени n.

В силу основной теоремы этот многочлен имеет хотя бы один корень, обозначим его через .Тогда в силу следствия теоремы Безу

,

где - многочлен - й степени; - также имеет корень, обозначим его через , тогда

,

- многочлен - й степени, который также имеет корень и т.д. Получим: , где - многочлен нулевой степени, - коэффициент при , получим:

.

Замечание. Многочлен n – й степени не может иметь более чем n различных корней.

Пример. Разложить на множители многочлен .

Решение: Найдем корни путем подбора.

Поделим заданный многочлен на .

5. Кратные корни многочлена.

Если в разложении многочлена n – й степени на линейные множители некоторые окажутся одинаковыми, то их можно объединить и тогда разложение будет иметь вид:

при этом и корень называется корнем кратности ; корень называется корнем кратности , и т.д.

Пример. Многочлен имеет корень кратности 2, второй корень - кратности 1.

Замечание. Все, что говорилось о корнях многочлена

можно сформулировать в терминах корней алгебраического уравнения .

 

 

6. Разложение многочлена на множители в случае комплексных корней.

 

Теорема. Если многочлен с действительными коэффициентами имеет комплексный корень , то он имеет и сопряженный корень .

Вывод. В разложении комплексные корни входят попарно-сопряженными.

Перемножив линейные множители, соответствующие паре комплексно-сопряженных корней получим трехчлен второй степени с действительными коэффициентами

,

где и действительные числа.

Например:

Если число является корнем кратности k, то сопряженное число должно являться корнем той же кратности k.

при этом .