Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки u &. В математической статистике, которая лежит в основе всех расчётов показателей выборочных совокупностей, доказывается, что значения средней ошибки выборки определяются по формуле:
где: 
m - средняя ошибка выборки;
s 2 генеральная дисперсия;
n - численность единиц выборочной совокупности.
Использование данной формулы предполагает, что известна генеральная дисперсия. Но при проведении выборочных исследований эти показатели, как правило, неизвестны. Применение выборочного метода как раз и предполагает определение характеристик генеральной совокупности.
На практике для определения средней ошибки выборки обычно используются дисперсии выборочной совокупности. Эта замена основана на том, что при соблюдении принципа случайного отбора дисперсия достаточно большого объёма выборки стремиться отобразить дисперсию в генеральной совокупности.
В математической статистике доказано следующее соотношение между дисперсиями в генеральной и выборочной совокупностях:

Из приведённой формулы видно, что дисперсия выборочной совокупности меньше дисперсии в генеральной совокупности на величину определяемую отношением:

Если n достаточно велико, то данное отношение близко к единице.
Например, при n = 100 оно равно 1,01, а при n = 500 оно равно 1,002. Поэтому с определённой долей погрешности формулу расчёта средней ошибки выборки можно представить в следующем виде.
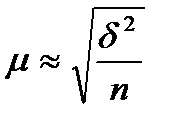
Однако следует иметь в виду, что данная формула применяется для определения средней ошибки выборки лишь при повторном отборе. Поскольку при бесповторном отборе численность генеральной совокупности N в ходе выборки сокращается, то в формулу для расчёта n средней ошибки выборки включают дополнительный множитель. Формула средней ошибки выборки принимает следующий вид:

Для практики выборочных обследований важно, что средняя ошибка выборки применяется для установления предела отклонений характеристик выборки из соответствующих показателей генеральной совокупности. Лишь с определённой степенью вероятности можно утверждать, что эти отклонения не превысят величины t u, которая в статистике называется предельной ошибкой выборки.
Предельная ошибка выборки связана со средней ошибкой выборки u отношением:

При этом t как коэффициент кратности средней ошибки выборки зависит от вероятности, с которой гарантируется величина предельной ошибки выборки. Обычно в практике экономических исследований обычно ограничиваются значением t не превышающим двух трёх единиц.
Задача 61
Темпы роста объема продукции текстильной промышленности в области за 1993 – 1997 годы характеризуются следующими данными (в процентах к предыдущему году):
| 106,3 | 105,2 | 106,1 | 106,3 | 105,5 |
Определите среднегодовой темп роста и прироста объема продукции за пятилетие (1993 – 1997 гг.)
| год | Продук. | ∆ | Тр, % | Тпр, % | |%| | |||
| ц | б | ц | б | ц | б | |||
| 106,3 | - | - | - | 100,0 | - | - | - | |
| 105,2 | -1,1 | -1,1 | 98,9 | 98,9 | -1,8 | -1,8 | 1,063 | |
| 106,1 | 0,9 | -0,2 | 100,8 | 99,8 | 0,8 | -0,2 | 1,052 | |
| 106,3 | 0,2 | 100,2 | 100,0 | 0,2 | - | 1,061 | ||
| 105,5 | -0,8 | -0,8 | 99,2 | 99,2 | -0,8 | -0,8 | 1,063 |
За базу взят показатель 1993 г. - 106,3
∆iц = yi – yi-1 Тр =  * 100%
* 100%
∆iб = yi – y0 Тпр =  * 100%
* 100%
Тпрiц(б) = Трiц(б) – 100%
Прирост объема продукции за пятилетие:
6,3 + 5,2 + 6,1 + 6,3 + 5,5 = 29,4
Среднегодовой темп роста за пятилетие:
29,4: 5 = 5,88
Задача 32
Определите среднюю длину пробега автофургона торговопосреднической фирмы и вычислите все показатели, если известны:
| Длина пробега за 1 рейс, км x | Число рейсов за квартал f | Xср | Xf |
| 30 – 50 | |||
| 50 – 70 | |||
| 70 – 90 | |||
| 90 – 110 | |||
| 110 – 130 | |||
| 130 – 150 | |||
| Всего: |
Xср = 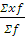 =
=  = 77,6087 км.
= 77,6087 км.
Задача 38
Автобус прошел путь в одном направлении со скоростью 68 км/ч, а в обратном со скоростью 52 км/ч. Определить среднюю скорость движения автобуса.
Xср =  = 60 км/ч
= 60 км/ч