Правило счета
Целые числа в любой системе счисления порождаются с помощью правила счета: Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Пример 1. Применяя правило счета, запишем первые десять целых чисел:
· в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
· в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
· в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
· в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Алгоритмы перевода чисел из одной позиционной системы исчисление в другую
Чтобы перевести целое десятичное число в двоичную (восьмеричную, шестнадцатеричную) систему счисления, нужно последовательно делить с остатком это число, а затем получаемые частные на основание новой системы счисления до тех пор, пока частное не станет меньше основания. При переводе запись двоичного (восьмеричного, шестнадцатеричного) числа следует начинать со старшего значащего разряда, а заканчивать записью младшего значащего разряда (см. пример 2).
Для перевода правильной дроби из десятичной системы счисления в двоичную (восьмеричную, шестнадцатеричную) нужно умножить исходную дробь и дробные части получающихся произведений на основание, представленное в десятичной системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в двоичной (восьмеричной, шестнадцатеричной) системе счисления (см. пример 3).
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Пример 2. Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Пример 3. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Обратный перевод числа в десятичную систему осуществляется по формуле:
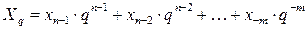
где:  – i -я цифра числа;
– i -я цифра числа; 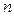 – количество цифр в целой части числа;
– количество цифр в целой части числа;  – количество цифр в дробной части числа;
– количество цифр в дробной части числа;  – основание системы счисления.
– основание системы счисления.
Пример 4. Выполним перевод числа  из двоичной системы счисления в десятичную.
из двоичной системы счисления в десятичную.
Имеем:  .
.
Чтобы перевести восьмеричное (шестнадцатеричное) число в двоичную систему, нужно заменить каждую цифру восьмеричного (шестнадцатеричного) числа соответствующим трехразрядным (четырехразрядным) двоичным числом. Затем необходимо удалить крайние нули слева, а при наличии точки – и крайние нули справа.
Пример 5.

Чтобы перевести двоичное число в восьмеричную (шестнадцатеричную) систему счисления нужно двигаясь от точки влево, а затем вправо, разбить двоичное число на группы по три (четыре) разряда, дополняя, при необходимости, нулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов следует заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (см. таблица 1).
Пример 6.
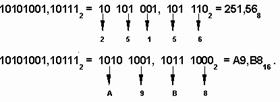
Таблица 1
Первые 16 натуральных чисел записанных в десятичной,
двоичной, восьмеричной и шестнадцатеричной системах счисления
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Операция сложения в позиционных системах счисления
Рассмотрим операцию сложения. Правила выполнения этой операций в десятичной системе хорошо известны – это сложение столбиком. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения надо пользоваться особыми для каждой системы.
Таблицы сложения легко составить, используя правило счета:
1) Сложение в двоичной системе

2) Сложение в восьмеричной системе

3) Сложение в шестнадцатеричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 7. Сложим числа 15 и 6 в различных системах счисления.

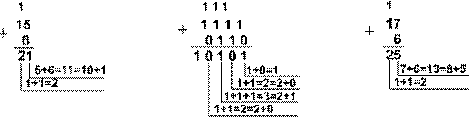
Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516.
Проверка. Преобразуем полученные суммы к десятичному виду:
101012 = 24 + 22 + 20 = 16+4+1=21,
258 = 2. 81 + 5. 80 = 16 + 5 = 21,
1516 = 1. 161 + 5. 160 = 16+5 = 21.