МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра высшей математики
УТВЕРЖДАЮ:
Первый проректор −
проректор по учебной работе
_____________ Е.А.Кудряшов
«____»___________2011г.
Аналитическая геометрия
Индивидуальные задания и методические указания
по выполнению модуля
Курск 2011
УДК 510 (083)
Составители: Е.В. Журавлева, А.В. Бойков
Рецензент
Кандидат физ.-мат. наук, доцент кафедры
высшей математики В.И. Дмитриев
Аналитическая геометрия: Индивидуальные задания и методические указания по выполнению модуля 13 / Юго-Зап. гос. ун-т; сост.: Е.В.Журавлева, А.В.Бойков. Курск, 2011. с. табл. 1. Библиогр.: с.50.
Методическая разработка содержит теоретические упражнения и практические задания по теме «Аналитическая геометрия». Индивидуальные задания разбиты на три уровня сложности. Представлены примеры решения наиболее сложных задач.
Предназначен для студентов технических и экономических специальностей.
Текст печатается в авторской редакции
Подписано в печать _______. Формат 60х84 1/16.
Усл. печ. л.. Уч.-изд. л..Тираж 50 экз. Заказ. Бесплатно.
Юго-Западный государственный университет.
305040 Курск, ул. 50 лет Октября, 94.
Содержание
Введение……………………………………………………………..4
1. Индивидуальные задания………………………………………..6
1.1. Теоретические упражнения.……………………………....6
1.2. Практические задания……………………………………10
1.2.1. Задание 1……………………………………………10
1.2.2. Задание 2…………………………………………....10
1.2.3. Задание 3………………………………………..…..14
1.2.4. Задание 4…………………………………………....26
1.2.5. Задание 5………………………………………..…..27
1.2.6. Задание 6……………………………………………27
1.2.7. Задание 7…………………………………………....35
1.2.8. Задание 8……………………………………………35
1.2.9. Задание 9……………………………………………37
2. Образцы выполнения некоторых заданий…………………….42
3. Контрольные вопросы…………………………………….…….50
Библиографический список ……………………………………52
Введение
Для аналитической геометрии определяющим является не предмет, а метод. Сущность этого метода заключается в том, что геометрическим объектам сопоставляются некоторым стандартным способом уравнения (системы уравнений) так, что геометрические отношения фигур выражаются в свойствах их уравнений.
В предлагаемых методических указаниях приводятся задания к типовому расчету по курсу “Аналитическая геометрия”, которые содержат теоретические и практические упражнения, контрольные вопросы. В разделе 2 приведены образцы выполнения наиболее сложных заданий, рекомендуемая структура отчета по типовому расчету и замечания по его оформлению.
Предусмотрены три уровня сложности заданий типового расчета. Номера заданий определяются по номеру варианта n (1≤ n ≤100).
Студенты, выбравшие задания первого уровня, выполняют теоретические упражнения с номером (n-1)(mod 18)+1 и практические упражнения 1; 2 (а-д); 3; 4 (а-е, и-л); 5; 6; 9.
Студенты, выбравшие задания первого уровня, выполняют теоретические упражнения с номерами (n-1) (mod 18)+1, (n+5) (mod 18)+1 и практические упражнения 1-3; 4 (кроме м); 5; 6; 7; 9.
Студенты, выбравшие задания третьего уровня, выполняют теоретические упражнения с номерами (n-1)(mod 18)+1, (n+5)(mod 18)+1, (n+12)(mod 18)+1 и все практические упражнения.
При выполнении задания рекомендуется использовать следующую литературу:
Теоретические упражнения
№1. [1; §7], [3; гл. 1; §3; п.3], [7; гл.1; §1.1].
№2. [1; §7], [3; гл. 1; §3; п.3].
№3. [3; гл. 5, §1; §2; п.5; Доп. к гл.1; п.8].
№4. [3; гл. 2, §3; пп.3,6; Доп. к гл.1; п.8].
№5. [3; гл. 5, §3; п.4; Доп. к гл.1; п.4].
№6. [3; гл. 5, §5; п.10].
№7. [3; гл. 5, §5].
№8. [3; гл. 5, §5; п.8].
№9. [3; гл. 5, §4; п.5; 5; п.9].
№10. [3; гл. 5, §4; п.5].
№11. [3; гл. 5, §4; п.1].
№12. [3; гл. 2, §3; пп.3,6; Доп. к гл.1, п.4].
№13. [3; гл. 2, §3; п.3].
№14. [3; гл. 2, §3; п.4].
№15. [3; гл. 4, §1], [5; гл. 2, §3; п.1; §4; п.1 ].
№16. [1; §24], [7; гл. 1, §1.7].
№17. [1; §24], [7; гл. 1, §1.7].
№18. [1; §25], [3; гл. 6, §3].
Практические упражнения:
№1. [1; §7], [3; гл.1; § 0; п.3], [2; гл.1; §1], [7; гл.1; §1.1].
№2. [1; §7-8], [3; гл.5; § 1-2], [2; гл.1; §1-2], [7; гл.1; §1.3].
№3. [1; §7-8], [3; гл.5; § 1-2], [2; гл.1; §1-2], [7; гл.1; §1.1-1.3].
№4. [1; §9-10], [3; гл.5; § 3-5], [2; гл.3; §1], [7; гл.4; §4.1-4.3].
№5. [1; §9-10], [3; гл.5; § 3-5], [2; гл.3; §1], [7; гл.4; §4.1-4.3].
№6. [1; §24], [3; гл.6; § 1-3], [2; гл.1; §3], [7; гл.1; §1.4].
№7. [1; §24], [3; гл.6; § 1-3], [2; гл.1; §3-4], [7; гл.1; §1.2, 1.4].
№8. [1; §24], [3; гл.6; § 3; п.5], [2; гл.1; §1, 3-4], [7; гл.1;
§1.4-1.6].
№9. [1; §25], [3; гл.7; § 1-3], [2; гл.3; §2], [7; гл.4; §4.4-4.5].
Контрольные вопросы:
[1; §5, 7-10, 24-25], [3; гл.1-7], [9; гл.1-00].
Индивидуальные задания
Теоретические упражнения
1. Доказать, что координаты точки A(x; y; z), делящей отрезок A1A2 в отношении λ1:λ2, выражаются формулами:
,
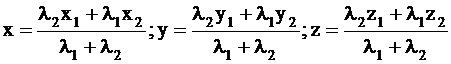где A1(x1;y1;z1) и A2(x2;y2;z2); λ1>0; λ2>0.
2. Центром тяжести двух масс m1, m2, расположенных в точках A1(x1;y1;z1) и A2(x2;y2;z2), называется точка А, делящая отрезок A1A2 в отношении m1:m2.
Найти координаты центра тяжести масс m1, m2. Найти координаты центра тяжести n масс mi, расположенных в точках A1(x1;y1;z1), 1=1,2,…,n.
3. Доказать, что три попарно непараллельные прямые
а1х + b1y + c1 = 0; a3x + b3y + c3 = 0;
a2x + b2y + c2 = 0,
имеют общую точку тогда и только тогда, когда
4. Доказать, что три точки А1(x1;y1), A2(x2;y2), A3(x3;y3) лежат на одной прямой тогда и только тогда, когда
5. Доказать, что плоскость, проходящая через три данные точки А1(x1;y1;z1), 1=1,2,3, задается уравнением
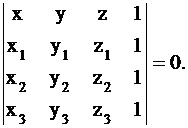
6. Доказать, что уравнение плоскости, проходящей через точки А1(x1;y1;z1) и А2(x2;y2;z2) перпендикулярно плоскости Ax + By + Cz + D = 0, можно записать в виде
7. Доказать, что плоскость, проходящая через точку А0(x0;y0;z0) и перпендикулярная плоскостям
A1x+B1y+C1z+D1=0; A2x+B2y+C2z+D2=0,
задается уравнением
8. Доказать, что плоскость, проходящая через прямую
и точку А0(x0;y0;z0), не лежащую на этой прямой, задается уравнением
9. Доказать, что уравнение плоскости, проходящей через пересекающиеся прямые
можно записать в виде
10. Доказать, что необходимым и достаточным условием принадлежности двух прямых
одной плоскости является выполнение равенства
11. Доказать, что уравнение прямой, проходящей через точку А0(x0;y0;z0) параллельно плоскостям A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 можно записать в виде
.
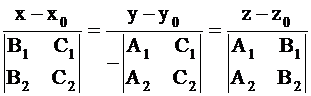12. Дан треугольник АВС, где А(x1;y1), В(x2;y2), С(x3;y3). Доказать, что площадь треугольника определяется формулой
13. Доказать, что расстояние от точки А до прямой, проходящей через точку В и имеющей направляющей вектор 
, определяется формулой
.
14. Даны две скрещивающиеся прямые, проходящие соответственно через точки А и В. Их направляющие векторы 
, 
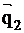известны. Доказать, что расстояние между прямыми определяется формулой
.
15. Доказать, что линия, задаваемая уравнением вида
x2+y2+2ax+2by+c=0,
где a2+b2-d >0, есть окружность. Найти координаты ее центра и радиус. Аналогично доказать, что поверхность, задаваемая уравнением вида
x2+y2+z2+2ax+2by+2cz+d=0,
где a2+b2+с2-d >0, есть сфера. Найти координаты ее центра и радиус.
16. Доказать, что эллипс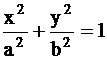 
допускает параметрическое задание
17. Доказать, что гипербола 
допускает параметрическое задание
(правая ветвь)
(−∞ < t < +∞)
(левая ветвь)
18. На плоскости задана прямая D и точка F, не лежащая на прямой D. Множество Ф точек М плоскости обладает тем свойством, что отношение е расстояния r от точки М до точки F к расстоянию d от точки М до прямой D постоянно и отлично от нуля. Доказать, что:
1) если е < 1, то фигура Ф-эллипс;
2) если е = 1, то фигура Ф-парабола;
3) если е > 1, то фигура Ф-гипербола.
Какой геометрический смысл имеют для этих кривых: точка F; прямая D; расстояния r,d; число е?
Практические задания
Индивидуальные условия заданий приведены в таблицах раздела 1 и определяются по номеру варианта n, а также с помощью параметров:
; 
; 
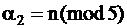, где
р(mod q) – остаток от деления p на q.
Задание 1
На плоскости даны точки 
и 
Найти:
а) точку С(x1;y1) – середину отрезка АВ;
б) точку D(x2;y2), которая делит отрезок АВ в отношении p:q. Параметры p,q приведены в табл.1.1.
Таблица 1.1
Параметры p,q к заданию 1
| n(mod 10) | p | q | n(mod 10) | p | q |
Задание 2
На плоскости даны точки А(x1;y1), В(x2;y2) и С(x3;y3). Сделайте чертеж треугольника АВС и найдите:
а) длину и уравнение стороны ВС (записать общее уравнение, каноническое, параметрическое и с угловым коэффициентом);
б) косинус угла А и угол А (в градусах);
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведенную к стороне ВС, и ее уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) уравнение биссектрисы угла А;
ж) координаты центра и радиус вписанной окружности;
з) координаты центра и радиус описанной окружности;
и) площадь треугольника;
к) координаты центра (тяжести) треугольника.
Таблица 1.2
Координаты точек А, В, С к заданию 2
| n | x1 | y1 | x2 | y2 | x3 | y3 |
| -1 -7 -1 -5 -1 -5 -2 -3 -3 -9 -7 -2 -1 -7 | -1 -2 -1 -2 -6 -6 -11 -7 -4 -9 -1 -3 -6 -1 | -1 -3 -1 -5 -5 -9 -7 -2 -7 | -1 -2 -2 -2 -5 -4 | -5 -5 -4 -3 -7 -3 -7 -1 -11 -14 -9 -2 -8 | -1 -2 -1 -3 -3 -5 -1 -4 |
Продолжение табл.1.2
| -6 -5 -5 -1 -3 -7 -1 -3 -7 -5 -2 -4 -3 -2 -6 -1 -5 -3 -3 | -1 -3 -8 -4 -1 -1 -9 -3 -8 -5 -2 -6 -9 -2 | -14 -7 -1 -9 -8 -4 -7 -8 -7 -1 -7 -2 -6 -2 -5 -11 -11 | -2 -1 -4 -6 -9 -7 -1 -1 -1 -1 -3 -1 -3 -6 -2 -1 | -6 -1 -3 -3 -3 -4 -1 -7 -1 -7 -5 -14 -1 -8 -11 | -8 -2 -3 -7 -1 -3 -1 -6 -6 -3 -5 -8 -9 -2 |
Продолжение табл.1.2
| -4 -1 -1 -2 -3 -8 -3 -11 -14 -1 -6 -9 -7 -7 -3 -7 -3 -3 -8 | -6 -3 -2 -3 -6 -3 -1 -7 -1 -5 -1 -5 | -3 -7 -1 -3 -7 -3 -7 -5 -4 -8 -6 -6 -3 -3 -3 -3 -5 -5 -1 | -3 -7 -6 -1 -6 -10 -5 -6 -1 -6 -9 -8 -8 -8 -1 -1 -7 -5 -11 -1 -4 -1 -1 | -3 -2 -5 -8 -6 -7 -3 -1 -2 -11 -1 -5 | -11 -7 -3 -7 -1 -1 -18 -4 -5 -6 -1 -9 -3 -6 -1 -4 -2 | |||
| ||||||||
| -7 -13 -3 -8 | -2 | -1 -1 | -4 -1 -4 -3 | -7 -7 -3 | -2 |
Задание 3
Решить планиметрическую задачу (см. табл. 1.3)
Таблица 1.3
Задачи к заданию 3
| n | Условие задачи |
На прямой 2x + y + 11 = 0 найти точку, равноудаленную от двух данных точек А(1;1), В(3;0)
Найти координаты точки, симметричной точке (2; -4) относительно прямой 4x + 3y +1 = 0.
Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x + y – 1 = 0 и y + 1 = 0, если известно, что диагонали параллелограмма пересекаются в точке Р(-1;0).
Составить уравнение прямой, проходящей через точку А(2;6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед.
Составить уравнение прямой, проходящей через точку А(-1;2) так, что середина ее отрезка, заключенного между параллельными прямыми x + 2y + 1 = 0 и x + 2y – 3 = 0, лежит на прямой x – y – 6 =0.
Даны уравнения двух сторон треугольника 4x – 5y + 9 = 0 и  . Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1)
|
Продолжение табл.1.3
| Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2x – y + 4 = 0 и 2x – y + 10 = 0 и уравнение одной из его диагоналей х + y + 2 = 0 Составить уравнения сторон треугольника, если А(-5;5), В(3;1) – две его вершины, а D(2;5) – точка пересечения его высот Дано уравнение одной из сторон квадрата x + 3y – 7 = 0 и точка пересечения его диагоналей Р(0; -1). Найти уравнения трех остальных сторон этого квадрата Даны уравнения одной из сторон ромба x – 3y + 10 = 0 и одной из его диагоналей x + 4y – 4 = 0. Диагонали ромба пересекаются в точке Р(0;1). Найти уравнения трех остальных сторон ромба Уравнения двух сторон параллелограмма x + 2y + 2 = 0 и x + y – 4 = 0,а уравнение одной из диагоналей х – 2 = 0. Найти координаты вершин Даны вершины А(-3; -2) и В(8; -4) трапеции ABCD (AD||BC). Известно, что диагонали трапеции равны и точка пересечения диагоналей О(0;2). Найти координаты вершин С и D этой трапеции Даны вершины А(2; -2) и В(3; -1) и точка Р(1;0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину С Даны уравнения двух высот треугольника 3x + 2y – 34 = 0 и x + y – 1 = 0 и одна из вершин А(6;5). Составить уравнения сторон Даны уравнения двух медиан 2x – 11y + 28 = 0 и 5x + 7y – 22 = 0 и одна из вершин (-2; -2) треугольника. Составить уравнения сторон |
Продолжение табл.1.3
| Две стороны треугольника заданы уравнениями 2x + y – 1 = 0 и x – 3y + 14 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны Даны уравнения сторон треугольника: (АВ) 7x – 2y + 32 = 0; (АС) x + y + 2 = 0; (ВС) 4x + y + 1 = 0. Найти точку пересечения его высот Составьте уравнения катетов прямоугольного равнобедренного треугольника, если уравнение гипотенузы 3x – y + 11 = 0 и С(4;3) – вершина прямого угла В равнобедренном треугольнике известны: уравнение основания 5x + 3y – 53 = 0, уравнение одной из боковых сторон x + 4y – 14 = 0 и точка на второй боковой стороне (3;7). Найдите уравнение второй боковой стороны Одна из сторон квадрата лежит на прямой x – 5y + 32 = 0, а одна из вершин находится в точке (8;1). Найдите уравнения остальных сторон квадрата Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4x – 7y + 28 = 0, концы которого лежат на осях координат Точки К(1;3) и L(-1;1) являются серединами оснований равнобедренной трапеции, а точки Р(3;0) и Q(-3;5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции Даны стороны треугольника: (АС) 2x – 15y – 55 = 0; (AB) 4x – 3y + 25 = 0; (BC) 14x + 3y – 61 = 0. Составить уравнение прямой, проходящей через вершину С и через точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4 Точки В(7;1) и D(9; -3) являются противоположными вершинами квадрата. Определить координаты двух других вершин |
Продолжение табл.1.3
| В треугольнике известны уравнения высоты x + y – 3 = 0 и медианы 11x – 4y + 10 = 0, проведенных из различных вершин. Написать уравнения сторон треугольника, зная одну его вершину (8;9). Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты 11x – 9y + 75 = 0 и биссектрисы 11x – 13y + 79 = 0, проведенных из одной вершины Точка А(2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой x + y – 1 =0. Составить уравнения двух других сторон Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в точке М(1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба Точка А(1;2) является серединой одного из оснований прямоугольной трапеции, а точка В(3; -1) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x – 3y + 10 = 0. Составить уравнения остальных сторон трапеции Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы x + y – 5 =0 и медианы x – y = 0, проведенных из различных вершин Даны координаты двух вершин треугольника А(-1;3), В(2;5) и ортоцентр – точка Н(1;4). Найти координаты третьей вершины треугольника. (Ортоцентром треугольника называется точка пересечения его высот) Точка Н(-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2x – y = 0 и x + y – 3 =0. Составить уравнение третьей стороны |
Продолжение табл.1.3
| Найти радиус и координаты центра окружности, проходящей через точку А(-1;3) и касающейся прямых 7x + y = 0 и x – y + 8 = 0 Окружность проходит через точки М(1;0) и N(2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5x – y – 4 = 0 Точки В(1;2) и С(3; -6) симметричны относительно некоторой прямой. Составить уравнение этой прямой Диагонали параллелограмма пересекаются в точке К(-2;4). Составить уравнение диагонали, не проходящую через точку пересечения сторон 4x – y + 4 = 0 и 4x +3y +20 = 0 Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку А (-4;8) Составить уравнение прямой L1, параллельной прямой L2: 2x + 3y – 23 = 0, если середина отрезка прямой L3: 5x +2y +3 = 0, заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 5x – y + 24 = 0 Составить уравнение стороны треугольника, в котором известны точка пересечения медиан (-1;7) и уравнения двух других сторон x + 4y – 37 = 0; 2x – y + 16 = 0 Даны две стороны x – y + 5 = 0 и x – y + 10 = 0 и диагональ 3x + y – 10 = 0 ромба. Найти вершины ромба В треугольнике известны две вершины А(-2;9), В(2; -3) и точка пересечения высот О(2;7). Написать уравнения сторон Точка А(3; -2) является вершиной квадрата, а точка М(1;1) – точкой пересечения его диагоналей. Составить уравнения сторон квадрата |
Продолжение табл.1.3
| Даны уравнения одной из сторон ромба x + y – 39 = 0 и одной из его диагоналей x – 3y + 11 = 0. Найти уравнения остальных сторон ромба Найти координаты вершин параллелограмма, в котором известны две стороны 2x – 5y – 5 = 0 и 2x + 5y – 15 = 0 и диагональ 6x + 5y – 35 = 0 Найти координаты точек С и D четырехугольника ABCD, в котором отрезки АВ и DC параллельны, BD и АС перпендикулярны друг другу и заданы вершины А(9; -1), В(5;5) Даны две вершины (3; -1), (1;4) и центр тяжести (0;2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон Даны уравнения двух высот треугольника 3x + 4y – 23 = 0 и 12x – 5y – 24 = 0 и одна из его вершин (1;1). Составить уравнения сторон Написать уравнения сторон треугольника, две медианы которого лежат на прямых x + y – 3 = 0 и 2x + 3y – 1 = 0, а точка А(1;1) является вершиной треугольника Две стороны треугольника заданы уравнениями, x + 3y – 21 = 0 и 7x + y + 13 = 0, а середина третьей стороны – точка (2;3). Составить уравнение третьей стороны Даны уравнения сторон треугольника: (MN) 3x – 5y + 17 = 0, (NP) 8x + 6y – 32 = 0, (МР) 5x + 11y + 9 = 0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот) |
Продолжение табл.1.3
Гипотенуза прямоугольного треугольника лежит на прямой 2x + y – 2 = 0, а точка С(3; -1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты
Основание равнобедренного треугольника лежит на прямой x + 2y – 2 = 0, а одна из боковых сторон – на прямой y + 2x – 1 =0. Составить уравнение другой боковой стороны треугольника, зная, что ее расстояние от точки пересечения данных прямых равно 
Составить уравнения сторон квадрата, в котором одна из вершин – точка (8;7) и одна из сторон лежит на прямой 5x + 2y + 4 = 0
Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2x + y – 8 = 0, концы которого лежат на окружности (х – 3)2 + y2 = 4
Точки М(3;7) и N(2;3) являются серединами оснований равнобедренной трапеции. Точки К(1;7) и Р(4;6,5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции
Даны стороны треугольника: (АВ) 4x + 3y – 10 = 0; (ВС) 3x + 2y – 8 = 0; (АС) 8x + 5y – 18 = 0. Составить уравнение прямой, проходящей через точку С и делящей сторону АВ в отношении 2:3 (считая от вершины А)
Противоположными вершинами квадрата являются точки
(-5;-3) и (3;17). Найти координаты двух других вершин
Написать уравнения сторон треугольника, зная одну его вершину (2;7), уравнения медианы 9x + y + 4 = 0 и высоты x + 5y – 11 = 0, проведенных из различных вершин
|
Продолжение табл.1.3
Написать уравнения сторон треугольника, зная одну его вершину (-5;4), уравнения высоты 6x + y – 61 = 0 и биссектрисы 4x – 3y + 7 = 0
Точка М(6;4) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой 3x – y + 2 = 0. Найти уравнения остальных сторон треугольника
Длина стороны ромба с тупым углом 120º равна  . Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке (-4;6). Составьте уравнения сторон ромба
Точка Р(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2;3) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x + 3y + 1 = 0. Составить уравнения сторон
Составьте уравнения трех сторон треугольника, в котором медиана 3x + 2y – 6 = 0 и биссектриса x – y = 0 проведены не из вершины (4;0), а из двух других вершин
Даны стороны треугольника: 4x – 3y + 26 = 0(АВ); x + 2y + 1 = 0(АС); 7x + 3y – 37 = 0(ВС). Найти точку пересечения медианы, проведенной из вершины В и высоты, проходящей через вершину С
Найти радиус и координаты центра окружности, проходящей через точку А(-1;8) и касающейся прямых х + 10 = 0 и 4x – 3y + 10 = 0
Точка отстоит на одинаковых расстояниях от точек Р(7;8) и Q(1;2). Найти координаты точки К, если известно, что она лежит на прямой 4x – 5y + 27 = 0
|
Продолжение табл.1.3
Найти координаты точки N, симметричной точке М относительно прямой x + y – 5 = 0. Точка М отстоит от прямой на расстоянии вдвое большем, чем точка К(-2;7) и находится с ней по одну сторону от прямой, причем отрезок КМ перпендикулярен прямой
В параллелограмме две стороны заданы уравнениями x – 5y + 7 = 0 и 5x – 3y – 9 = 0. Составить уравнение диагонали параллелограмма, не проходящей через точку пересечения этих сторон, если известно, что диагонали пересекаются в точке М(2;4)
Найти координаты вершин треугольника, симметричного треугольнику АВС относительно центра описанной около треугольника АВС окружности, если А(9; −1), В(5;1), С(0; −5)
Составить уравнение прямой, перпендикулярной прямой x + 3y – 13 = 0 и образующей с осями координат треугольник, площадь которого равна 6
Составить уравнение прямой, проходящей через точку А(1;2) так, что отрезок этой прямой, заключенный между прямыми 3x + y + 2 = 0 и 4x + y – 1 = 0, в точке А делится пополам
Центр тяжести треугольника – точка  . Уравнения двух его сторон 4x + y + 14 = 0 и x – 6y – 9 = 0. Составить уравнение третьей стороны
Известны уравнения двух сторон ромба 7x – 9y – 39 = 0 и 3x + 11y – 91 = 0 и одной из его диагоналей 5x + y – 13 = 0. Вычислить координаты вершин ромба
Составить уравнение третьей стороны треугольника, если известны уравнения двух его сторон 6x – y – 11 = 0 и 4x + 5y + 13 = 0 и ортоцентр – точка (−1;2)
|
Продолжение табл.1.3
Написать уравнения сторон квадрата, центр которого – точка (1; -3), а одна из вершин – точка (-4;7)
Написать уравнения сторон ромба, если известны диагональ x + y – 2 = 0, точка ее пересечения с другой диагональю (0;2) и одна из сторон 3x – y – 10 = 0
Вычислить координаты вершин параллелограмма, в котором две стороны лежат на прямых 2x – 5y – 5 = 0 и 2x + 5y – 15 = 0, а одна из диагоналей на прямой 6x + 5y – 35 = 0
Диагонали трапеции ABCD (AD||BC) перпендикулярны друг другу и заданы вершины А(4; -1) и В(13;6). Найти координаты вершин С и D трапеции
Составить уравнения сторон треугольника, в котором даны две вершины (-7;6) и (7;4) и точка пересечения отрезков, соединяющих эти вершины с серединами противоположных сторон (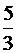 ; 4)
Даны уравнения двух высот треугольника x – 5y + 16 = 0 и 9x + 7y + 14 = 0 и одна из его вершин М(-5; -3). Написать уравнения сторон треугольника
Даны уравнения двух медиан x – 3y + 2 = 0 и 2x + 2y – 21 = 0 треугольника и одна из вершин (5; -1). Найти уравнения сторон треугольника
Середина одной из сторон треугольника – точка (0;3). Две другие стороны лежат на прямых x – 9y + 52 = 0 и x + y – 8 = 0. Составить уравнение третьей стороны
Найти точку пересечения высот треугольника, стороны которого лежат на прямых 6x + y – 23 = 0; 9x – 4y – 7 = 0; 3x – 5y – 17 = 0
|
Продолжение табл.1.3
Точка С(6;1) – вершина прямого угла в треугольнике, а гипотенуза лежит на прямой 2x – 3y + 5 = 0. Написать уравнения катетов, один из которых лежит на прямой, содержащей точку (-4; −25)
Точки А(1;2) и В(3;0) – вершины равнобедренного треугольника АВС, углы А и В при основании равны  . Найти координаты вершины С, зная, что она лежит по ту же сторону от прямой АВ, что и точка М(2;3)
Составить уравнения сторон квадрата по известному уравнению одной из сторон x + 8y – 17 = 0 и одной из вершин (2;9)
Даны уравнения сторон квадрата 4x + y – 9 = 0 и 4x + y + 36 = 0. Составить уравнения двух других его сторон при условии, что точка А(6;2) лежит на стороне этого квадрата
Точки М(5; -1) и N(-3;7) являются серединами оснований равнобедренной трапеции, а точки Р(-1; 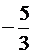 ) и К(4;6) лежат на боковых сторонах. Составить уравнения сторон трапеции
Даны стороны треугольника 9x – 2y – 51 = 0 (АС), 4x + 3y + 24 = 0 (АВ), x + 2y + 1 = 0 (ВС). Составить уравнение прямой, проходящей через вершину С и точку К на стороне АВ, делящую ее в отношении 3:7 (считая от вершины В)
Точки А(9;8) и D(-1;4) являются противоположными вершинами квадрата. Определить координаты других вершин
Известны одна из вершин треугольника (4; -5), уравнения высоты 7x – y + 17 = 0 и медианы 2x – 11y – 13 = 0. Составить уравнения сторон
|
Продолжение табл.1.3
Составить уравнения сторон треугольника, зная одну его вершину (4;1), уравнения высоты 2x – y + 11 = 0 и биссектрисы 7x – 8y + 25 = 0, проведенных из одной вершины
Стороны треугольника заданы уравнениями: 4x – 3y = 0 (АВ);
3x – 4y = 0 (ВС); 5x + 12y – 10 = 0 (АС). Найти радиус вписанной окружности
Известны уравнение одной из сторон правильного треугольника 5x – y + 1 = 0 и одна из вершин (5; -3). Составить уравнения двух других сторон треугольника
Диагонали ромба пересекаются в точке К(3; -7). Большая диагональ образует с осью ординат угол 45°, а со сторонами 30°. Длина стороны равна  . Составить уравнение сторон ромба
Точка М(6;1) является серединой одного из оснований прямоугольной трапеции, а точка N(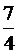 ; 1) – серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой x + 4y + 7 = 0. Составить уравнения остальных сторон трапеции
Из одной вершины треугольника проведена биссектриса 3x + y – 1 = 0, а из другой – медиана 11x – 5y – 25 = 0, а третья вершина – точка А(−3; −-2). Составить уравнения сторон треугольника
Ортоцентр треугольника – точка Q(-1;5). Составить уравнения сторон треугольника, если известны две его вершины А(2;1) и В(2;11)
Даны уравнения сторон треугольника x +2y+1 = 0; 2x–y–2 =0; 2x + у + 2 = 0. Найти точку пересечения высот
Найти координаты центра окружности, проходящей через точку А(-3;5) и касающейся прямых x – 3y – 2 = 0 и 13x – 7y + 102 = 0
|
Задание 4
В пространстве даны точки А(-2;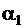 
;1), В(3; 
;-1), С(5; 
;1), S(1; 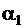;0). Сделать чертеж пирамиды SABC и найти:
а) длину и уравнение ребра АВ;
б) площадь и уравнение грани АВС;
в) высоту, проведенную из вершины S к грани АВС, и ее уравнение;
г) проекцию вершины S на плоскость АВС;
д) уравнение прямой, проходящей через вершину S параллельно ребру АВ;
е) уравнение плоскости, проходящей через вершину S параллельно грани АВС;
ж) уравнение плоскости, проходящей через ребро AS перпендикулярно грани АВС;
з) уравнение проекции ребра AS на грань АВС;
и) угол между ребрами АВ и AS;
к) угол между ребром AS и гранью АВС;
л) угол между гранями АВС и АВS;
м) координаты центра и радиус вписанной в пирамиду SABC сферы;
н) координаты центра и радиус описанной около пирамиды SABC сферы;
о) координаты центра (тяжести) пирамиды SABC;
п) объем пирамиды.
Задание 5
Дана точка М(1;0; -2). Найти:
а) точку М1(x1;y1;z1), симметричную точке М относительно точки 
;
б) точку М2(x2;y2;z2), симметричную точке М относительно прямой
;
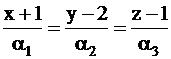в) точку М3(x3;y3;z3), симметричную точке М относительно плоскости 
.
Задание 6
Составить канонические уравнение кривой второго порядка (эллипса, гиперболы или параболы (см.табл.1.4), расположенной симметрично относительно декартовой системы координат, если … (доп. усл. см. табл.1.5). Построить кривую на чертеже и указать на нем фокусы и директрисы (для гиперболы еще и асимптоты) кривой.
Таблица 1.4
Индивидуальные условия к заданию 6
| MOD(n,3) | Кривая | Расположение кривой относительно декартовой прямоугольной системы координат |
| Эллипс Гипербола Парабола | Симметрично относительно начала координат. Фокусы лежат на оси Ох Симметрично относительно начала координат. Фокусы лежат на оси Ох Симметрично оси Оy. Фокусы лежат на оси Ох |
Таблица 1.5
Дополнительные условия к заданию 6
| n | Дополнительные условия |
большая полуось а = 3 и фокусы имеют координаты F( 2;0)
фокусы имеют координаты F( 5;0) и расстояние между директрисами равно 6
фокальный параметр равен 3,5 и парабола лежит в полуплоскости x >0
малая полуось b = 2 и уравнение директрис x = 4
фокальный параметр p = 5 и действительная полуось а = 6
уравнение директрисы x = -1,5
большая полуось а = 4 и фокальный параметр p = 6
действительная полуось а = 4 и расстояние между фокусами равно 10
точка М(-1;2) принадлежит кривой
фокальные радиусы вершин эллипса, лежащих на оси х, равны 1 и 11 (r1 = 1, r2 = 11)
фокусы имеют координаты F( 7;0) и уравнение директрис х = 4
фокус имеет координаты F( ;0)
малая полуось  и расстояние между фокусами равно 2
расстояние между фокусом и соответствующей ему директрисой p = 0,5 и фокусы имеют координаты F( 6;0)
уравнение директрисы x = 0,25
расстояние между фокусами равно 4 и расстояние между директрисами равно 6
действительная полуось равна 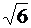 и эксцентриситет равен 
фокальный параметр p = 1,25 и парабола лежит в полуплоскости x <0
|
Продолжение табл.1.5
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-12 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |