При анализе временного ряда его изменчивость можно разделить на закономерную (детерминированную) и случайную составляющие. Для многих рядов в экономике причины, порождающие их закономерные составляющие не ясны. Тем не менее их совокупное влияние может быть устойчивым в течении достаточно длительных промежутков времени. Это обеспечивает возможность прогноза для подобных временных рядов.
Составная часть временного ряда, остающаяся после выделения из него закономерных (детерминированных) компонент, представляет собой случайную, нерегулярную компоненту. Она является обязательной составной частью любого временного ряда в экономике, так как случайные отклонения неизбежно сопутствуют любому экономическому явлению. Если систематические компоненты временного ряда определены правильно, что как раз и составляет одну из главных целей при разработке моделей временного ряда, то остающаяся после выделения из временного ряда этих компонент так называемая остаточная последовательность (ряд остатков) будет случайной компонентой ряда.
Случайная компонента ряда обладает следующими свойствами:
– случайностью колебаний уровней остаточной последовательности;
– соответствием распределения случайной компоненты нормальному закону распределения;
– равенством математического ожидания случайной компоненты нулю;
– независимостью значений уровней случайной последовательности, то есть отсутствием существенной автокорреляции.
Проверка адекватности моделей временных рядов основана на проверке выполняемости у остаточной последовательности указанных четырех свойств. Если не выполняется хотя бы одно из них, модель признается неадекватной; при выполнении всех четырех свойств модель адекватна. Данная проверка осуществляется с использованием ряда статистических критериев
|
|
Закономерную или детерминированную составляющую при анализе экономического временного ряда обычно разбивают на три составляющие: тренд,сезонную компонентуи циклическую компоненту.
Наличие первых двух составляющих временного ряда можно приблизительно определить визуально, построив график временного ряда. На рисунке 1.3 показаны различные виды временных рядов с трендом и сезонной составляющей.
Рисунок 1.3 – Различные виды временных рядов
На рисунке 1.3 введены следующие обозначения:
1 – временной ряд не содержит сезонной составляющей;
2 – временной ряд содержит аддитивную сезонную составляющую;
3 – временной ряд содержит мультипликативную сезонную составляющую;
А – временный ряд не содержит тренда;
В – временной ряд содержит аддитивный тренд;
С – временной ряд содержит мультипликативный тренд (при увеличении данных, увеличивается величина сезонных отклонений).
(Ниже в этом пункте будет рассмотрены понятия аддитивной и мультипликативной переменных временного ряда).
Циклическая компонента временного ряда описывает длительные периоды относительного подъёма и спада. Она состоит из циклов, которые меняются по амплитуде и протяженности. Выделение в экономических временных рядах циклической компоненты связано с тем, что экономическая активность не растет (или спадает) постоянными темпами. Она состоит из периодов относительных подъёмов и спадов. Считается, что причиной циклических изменений в экономических показателях является взаимодействие спроса и предложения. Играют роль и другие факторы: рост и истощение ресурсов, увеличение размеров капитала, используемого в бизнесе, продолжительно действующие неблагоприятные (либо благоприятные) для тех или иных отраслей сельского хозяйства погодные условия, изменения в правительственной финансовой и налоговой политике и т. п. Влияние всех этих факторов приводит к тому, что циклическую компоненту крайне трудно идентифицировать формальными методами, исходя только из данных изучаемого ряда. Поэтому для ее анализа обычно приходиться привлекать дополнительную информацию в виде других временных рядов, которые оказывают влияние на изучаемый ряд, например, учитывать информацию типа налоговых льгот, перенасыщенности рынка и т. п.
|
|
В ходе выполнения данной лабораторной работы необходимо будет учитывать влияние лишь двух составляющих: тренда и сезонной компоненты.
К сезонным относятся такие явления, которые обнаруживают в своем развитии определенные закономерности более или менее повторяющиеся из месяца в месяц, из квартала в квартал. Под сезонностью иногда понимают неравномерность производственной деятельности в отраслях промышленности, связанных с переработкой с/х сырья, поступления которого зависит от времени года. Кроме того, сезонность может возникать из-за сезонного характера спроса на товары, производимые промышленностью и т. д. Как бы ни проявлялась сезонность, она наносит большой ущерб народному хозяйству, который заключается в неравномерном использовании оборудования и рабочей силы, неравномерной постановке сырья и загрузке транспорта в отраслях, связанных с сезонным производством. Изучение сезонных колебаний необходимо для более ритмичной работы предприятий.
|
|
Статистическое исследование сезонности ставит следующие задачи: численно выразить проявление сезонных колебаний; выявить их силу и характер в условиях отдельных отраслей народного хозяйства; вскрыть факторы, вызывающие сезонные колебания; найти экономические последствия проявления сезонности. Известно несколько способов исследования сезонных колебаний: способ простых средних, способ относительных чисел, способ Персонса, способ расчета сезонных волн, базирующийся на определении тенденции (методом скользящей средней и методом наименьших квадратов).
Индексы сезонности являются показателями, характеризующими результаты сравнения фактических уровней данного месяца или квартала с уровнями, вычисленными при выявлении основной тенденции для того же месяца или квартала.
Расчет сезонного индекса может быть произведен следующим образом. Предположим, что рассматриваемый временной ряд x1, … xn может быть описан аддитивной моделью. Пусть p – период последовательности st. Для этого сначала мы должны оценить тренд 
. Затем для каждого сезона i, 1 
i p, необходимо рассмотреть все относящиеся к нему разности: xi – . Каждое из этих отклонений xi от можно рассматривать как результат влияния сезонных изменений. Усреднение этих разностей дает нам оценку сезонной компоненты si. В качестве простейшей оценки можно взять простое среднее, т.е.:
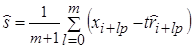для i = 1,…, p
Сезонный индекс для мультипликативной модели вычисляется по другой формуле.
Minitab производит классическую декомпозицию временного ряда, используя мультипликативную или аддитивную модели. С помощью этой процедуры временной ряд разделяется на три составляющие: тренд, сезонные колебания и ошибку.
Для работы с этим видом анализа необходимо набрать: Stat > Time Series > Decomposition. В результате выполнения этой процедуры на мониторе появится следующие диалоговое окно (рисунок 1.4).
Рисунок 1.4 – Вид диалогового окна "Анализ сезонной декомпозиции"
Диалоговое окно включает в себя следующие параметры:
Variable: выбирается столбец, содержащий исходный временной ряд.
Seasonal Length: Длина сезонного цикла. Вводится целое число большее 2.
Model Type: Выбирается тип модели:
– мультипликативная модель. Используется, если сезонные колебания зависят от уровня данных. В этом случае предполагается, что если данные увеличиваются, то увеличивается и величина сезонных отклонений. Многие временные ряды соответствуют этой модели. Модель имеет следующий вид
yt = Trend * Seasonal * Error
– аддитивная модель имеет следующий вид:
yt = Trend + Seasonal + Error
Model Components: Выбор компонентов присутствующих в модели:
– Trend plus seasonal: Отмечается, если исходные данные содержат тренд и сезонную составляющую.
– Seasonal only: Отмечается, если при анализе тренд не учитывается. Если данные содержат тренд, но это не указано, то оценки сезонных индексов могут быть не верными.
Initial seasonal period: По умолчанию Minitab считает, что исходные данные начинаются с первого периода – 1. Если исследуются месячные данные, и они начинаются с июня, то тогда указывается 6 месяц.
Generate forecasts: Отмечается, если необходимо сделать прогноз. Прогнозные значения отмечаются на графике красным цветом.
Number of forecasts: Вводится число прогнозных значений.
Starting from origin: Используется аналогично диалогу в анализе тренда.
Title: Можно ввести свое название графика.
Minitab при декомпозиции:
- оценивает линию тренда методом наименьших квадратов;
- удаляет тренд, деля на тренд или вычитая его из временного ряда в зависимости от используемой модели (соответственно мультипликативной или аддитивной);
- сглаживает преобразованные данные, используя метод скользящего среднего с параметром сглаживания равным длине сезонного цикла. Если сезонный цикл четный, то используется двухшаговая процедура сглаживания методом скользящего среднего;
- временной ряд без тренда делится или из него вычитается полученный сглаженный ряд, чтобы получить сезонную компоненту. С помощью полученных значений вычисляются сезонные индексы, которые позволяют оценить влияние сезонных колебаний.
Рассмотрим на примере производства молока процедуру декомпозиции временного ряда (данные представлены в таблице 1.2).
Таблица 1.2 – Производство молока в России за 1992–1996 гг. (тыс. тонн в месяц)
| Месяц \ год | 1992 г. | 1993 г. | 1994 г. | 1995 г. | 1996 г. |
| январь | |||||
| февраль | |||||
| март | |||||
| апрель | |||||
| май | |||||
| июнь | |||||
| июль | |||||
| август | |||||
| сентябрь | |||||
| октябрь | |||||
| ноябрь | |||||
| декабрь |
Заполним диалоговое окно, изображенное на рисунке 1.4, следующим образом:
Variable: 1992–96
Seasonal Length: 12
Model Type: мультипликативная модель (для выбора типа модели можно использовать рисунок 1.3. Из графика анализирующего временной ряд на наличие тренда (рисунок 1.5) видно, что величина сезонных колебаний пропорциональна среднему уровню производства. Поэтому для описания сезонных колебаний следует использовать мультипликативную модель).
Model Components: Trend plus seasonal (тренд и сезонная составляющая)
Initial seasonal period: 1 (данные начинаются с января)
Generate forecasts:
Number of forecasts: 6
В результате выполнения этой операции на экране появятся следующие графики и расчеты. В окне Session появятся результаты вычисления сезонных индексов и значения прогнозных показателей на полгода вперед, а также уравнение тренда и его точность:
Time Series Decomposition (Декомпозиция временного ряда)
Data 1992-96 (Название анализируемых данных)
Length 58.0000 (Длина временного ряда)
NMissing 0 (Количество ошибок в данных)
Trend Line Equation (Уравнение тренда)
Yt = 2841.10 - 23.6304*t
Seasonal Indices (Сезонные индексы)
| Period | Index |
| 0.654509 | |
| 0.678928 | |
| 0.909029 | |
| 1.02617 | |
| 1.27273 | |
| 1.58137 | |
| 1.54385 | |
| 1.35862 | |
| 1.02653 | |
| 0.777468 | |
| 0.570636 | |
| 0.600173 |
Accuracy of Model (Оценка точности полученного уравнения тренда)
MAPE: 4.1
MAD: 85.0
MSD: 10808.6
Forecasts (Прогнозные значения)
| Row | Period | Forecast |
| 826.68 | ||
| 855.31 | ||
| 917.31 | ||
| 935.52 | ||
| 1231.15 | ||
| 1365.59 |
При проведении декомпозиции Minitab также генерирует три набора графиков (рисунки 1.5 – 1.7).
На рисунке 1.5 изображены исходные данные, оцененная линия тренда, оцененная линия тренда с сезонными колебаниями (predicted) и прогнозные значения.
На рисунке 1.6 изображены отдельные графики для каждой компоненты: исходные данные, данные без тренда, данные без сезонных колебаний и график ошибки – данные без тренда и без сезонных колебаний.
Эта группа графиков показывает как сезонные колебания влияют на временной ряд. Сюда входят графики:
- сезонных индексов (Seasonal Indices),
- график процента дисперсии обусловленной сезонными колебаниями (Percent Variation, by Seasonal Period),
- график разброса исходных данных за рассматриваемый сезонный период (Original Data, by Seasonal Period),
- график разброса остатков за этот период (Residuals, by Seasonal Period).
Рисунок 1.5 – График временного ряда
Рисунок 1.6 – Результаты компонентного анализа при декомпозиции временного ряда.
Рисунок 1.7 – Результаты сезонного анализа при декомпозиции временного ряда
В результате проведенного анализа можно сделать следующие выводы:
1. Визуальный анализ графика ряда показывает, что производство молока имеет тенденцию к сокращению. Это может быть обусловлено сокращением поголовья молочного стада и общим снижением производства сельскохозяйственной продукции.
2. Временный ряд подвержен сильным сезонным колебаниям с максимумом производства в летние месяцы (апрель – сентябрь) и минимумом – в зимние (октябрь – март). При этом величина сезонных колебаний пропорциональна среднему уровню производства.
Следовательно, потребителю молочных продуктов необходимо быть готовым к сезонным изменениям уровня цен на продукцию: в летние месяцы — снижение цены, в зимние — возрастание.