ГЛАВА 4.ТРЕХФАЗНЫЕ ЦЕПИ
Трехфазные цепи при соединении звездой
Особенности трехфазных систем.
Трехфазная система переменного тока широко используется в силовых электротехнических и энергетических установках. Впервые такая система была продемонстрирована русским инженером М. О. Доливо-Добровольским в 1891 году при передаче энергии на электротехническую выставку во Франкфурте-на-Майне.
Трехфазная система переменного тока представляет собой совокупность трех отдельных цепей, объединенных в одну общую систему. Напряжения в такой системе имеют одинаковую амплитуду и сдвинуты между собой по фазе на 120°. При этом последовательность чередования фаз может быть прямой или обратной. При прямой последовательности напряжение каждой последующей фазы отстает от предыдущей на угол, равный 120°. При обратной последовательности напряжение каждой последующей фазы опережает предыдущую на угол, равный 120°.
В трехфазной системе используются специальные трехфазные генераторы. В энергетических установках применяются специальные трехфазные электромеханические генераторы, а в электротехнических установках - это различного рода статические инверторы.
Основными применениями трехфазных систем являются:
□ передача энергии на большие расстояния,
□ питание асинхронных трехфазных двигателей,
□ создание постоянных напряжений с малыми пульсациями,
□ питание электросварочного оборудования и т. д.
Трехфазные источники напряжения.
Трехфазные источники напряжения создают три напряжения, сдвинутые относительно друг друга на треть период (или угол, равный 2π/3). Форма этих напряжений может быть различной: синусоидальной, прямоугольной, многоступенчатой, импульсной с широтной модуляцией. Однако наибольшее распространение получили генераторы, которые создают три гармонических напряжения:
(4.1)
Схема такого генератора показана на рис. 4.1а. Генератор содержит три обмотки, в которых индуктируются три напряжения ЕА, ЕВ, ЕС, соединенные между собой в точке 0. Векторная диаграмма для прямого чередования фаз приведена на рис. 4.1 б, а для обратного - на рис. 4.1 е.
Рисунок 4.1
Мгновенные значения этих трех напряжений для прямого чередования фаз показаны на рис. 4.1 г.
Комплексные значения трех напряжений генератора в соответствии с (4.1) можно представить в виде
(4.2)
где Е - действующее значение напряжения генератора,
α = e2πj = еj120 - фазный множитель трехфазной системы (оператор поворота на 120°).
Очевидно, что умножение на α поворачивает вектор напряжения Е на угол, равный +120°. Аналогично, умножение на α-1 поворачивает вектор Е на угол -120°, что эквивалентно умножению на α2 = ej240. Сумма трех единичных векторов а0 + а] + а2 = 1 + а + а2 = 0.
Провода, соединяющие фазы генератора и приемника, называются линейными, а токи в них - линейными токами. Напряжения ЕА, Ев, Ес между началами и концами фаз генератора называются фазными Uф, а напряжения ЕВА, еас, Есв между началами фаз генератора - линейными Uл. Для симметричного трехфазного генератора Uл = √3Uф.
Соединение приемников звездой. Соединение приемников звездой представляет такое включение фаз приемника, при котором все начала (или концы) фаз соединены в один узел 0, называемый нулевой (или нейтральной)точкой приемника. На рис. 4.2, а показано соединение звездой фаз генератора ЕА, Ев, Ес, сопротивлений приемников ZA = rА + jxA, ZB = rB + JxB, Zc = rc+ jxc и сопротивления нулевого провода Z0 = r0 + jx0. Векторная диаграмма, cоответствующая такому включению, приведена на рис. 4.2, б.
Линейные и фазные напряжения приемника связаны между собой соотношениями:
(4.3)
Падение напряжения на сопротивлении Z0 нулевого провода определяется как напряжение между двумя узлами 0'-0.
(4.4)
где YA =1/ZA, YB =1/ZB, Yc= 1/ZC, У0 = 1/Z0 - проводимости фаз приемника и нулевого провода.
Если известны напряжения генератора и сопротивления фаз приемника,
Рисунок 4.2
то фазные напряжения определяются по формулам:
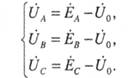(4.5)
Токи в фазах приемника IА,Iв,Iс имеют значения
(4.6)
Аналогично определяется ток в нулевом проводе
(4.6а)
При отсутствии нулевого провода следует принять Y0 = 0. Ток в нулевом проводе равен сумме фазных токов
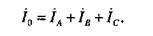(4.7)
Теперь перейдем к рассмотрению различных режимов работы трехфазной системы при соединении генераторов и приемников звездой с нулевым и нулевого провода.
Равномерная нагрузка фаз генератора. При равномерной нагрузке фаз генератора проводимости нагрузки YA = YB = Yc = Yn и, следовательно, из уравнений (25.6), (25.7) находим, что
(4.8)
Отсюда следует, что при равномерной нагрузке фаз напряжение между нулевыми точками генератора и нагрузки U0 = 0 при любом сопротивлении нулевого провода, в том числе и при его отсутствии.
Кроме того, фазные напряжения генератора равны фазным напряжениям приемника
Векторная диаграмма при равномерной нагрузке фаз генератора приведена на рис. 4.3, а. При симметричной системе напряжений генератора линейные и фазные напряжения приемника связаны соотношением Uл =√3Uф, а линейные токи равны фазным Iл =I ф.
Очевидно, что при равномерной нагрузке фаз нулевой провод можно исключить без изменения при этом токов и напряжений приемников.
Неравномерная нагрузка фаз генератора. При неравномерной нагрузке фаз генератора следует рассматривать два случая: при наличии или отсутствии нулевого провода. Если нулевой провод присутствует, то токи в нагрузках и нулевом проводе определяются по формулам (4.6). При этом напряжения на нагрузках можно определить по формулам (4.5), а напряжение на нулевом проводе - по формуле (4.4).
Если сопротивление нулевого провода принять равным нулю (Z0 = 0), то напряжение U {) = 0 и, следовательно, фазные напряжения приемника равны фазным напряжениям генератора
При этом ток в нулевом проводе определяется по формуле (4.7). Векторная диаграмма для этого случая приведена на рис. 4.3,б.
Если нулевой провод отсутствует (Y0 = 0), то нулевое напряжение определится по формуле
При этом фазные напряжения приемника не равны фазным напряжениям генератора и определяются выражениями (25.5). Векторная диаграмма для этого случая приведена на рис. 4.3, в.
Рисунок 4.3
Если известны линейные напряжения UAB,UBC,UCA, то фазные напряжения можно вычислить по формулам
(4.9)
Короткое замыкание фазы приемника. Короткое замыкание фазы приемника является по своей сути частным случаем неравномерной нагрузки фаз генератора. При наличии нулевого провода короткое замыкание любой фазы приводит к аварийной ситуации, так как ток в этой фазе резко увеличивается.
Короткое замыкание одной из фаз приемника при отсутствии нулевого провода не приводит к аварийной ситуации, так как линейные напряжения сети прикладываются в этом случае к двум другим фазам приемника.
Так, например, при коротком замыкании фазы А напряжение на ней становится равным нулю U А = 0, анапряжения двух других фаз становятся равными линейным напряжениямUв = -UAB,UC = UCA, т.е. увеличиваются в √3 раз. Соответственно во столько же раз увеличиваются и значения токов этих фаз. При этом фазный ток замкнутой фазы увеличивается и становится равным IA = - (IВ + Iс). Нулевое напряжение становится равным фазному напряжению генератора U0= ЕА. Векторная диаграмма для этого случая приведена на рис. 4.3, г.
Обрыв линейного провода. Если в трехфазной системе с нулевым проводом произойдет обрыв одного линейного провода, то это приведет к исчезновению тока и напряжения в этой фазе. Напряжения на неповрежденных фазах не изменятся. Так, например, при обрыве фазы А ток в этой фазе становится равным нулю [IA = 0). Ток в нулевом проводе будет равен I0 = (Iв+Iс). Векторная диаграмма для этого случая приведена на рис. 4.3, д.
При обрыве линейного провода в трехфазной системе без нулевого провоза неповрежденные фазы оказываются соединенными последовательно и подученными к одному линейному напряжению. Так, например, при обрыве фазы А неповрежденные фазы В и С оказываются включенными последовательно на напряжение UBC, т. е. U BC = UB-UC. При этом напряжения на фазах B и С распределяются пропорционально их сопротивлениям ZB, Zc. Векторная диаграмма для этого случая приведена на рис. 4.3, е.
Пример1. Требуется определить токи в фазах приемника, соединенного звездой без нулевого провода, если сопротивления нагрузок имеют значения ZA = 5 Ом,ZB=ZC=10 Ом, а фазное напряжение генератора Е = 100 В. Построить векторную диаграмму для токов в цепи.
Решение. Определим нулевое напряжение, пользуясь формулой (4.4). Поскольку два сопротивления нагрузки имеют одно и то же значение ZB=ZC, то формула (26.4) несколько упрощается. Учитывая, что а = еj120° =(-1 +j√3)/2 и а-1=е-j120° =(-1-j√3)/2, получим из формулы (4.4)
Найдем напряжения на фазах приемника
Определим токи в фазах приемника:
Векторная диаграмма, соответствующая полученному решению, приведена на рис. 4.4.
Рисунок 4.4