Трехфазные цепи при соединении треугольником

Особенности включения трехфазных систем треугольником. При соединении трехфазных систем треугольником также используются три гармо­нических напряжения (4.1), которые были рассмотрены в лекции 15. Однако соединение этих источников выполняется таким образом, что начало одной фазы соединяется с концом другой. На рис. 4.5 а показано такое включение трех обмоток генератора и соответствующее ему включение источников напряжения .

Векторная диаграмма для, соединения обмоток генератора по схеме треугольника приведена на рис. 4.5, б. На этой диаграмме полагается, что вектора напряжений генератора имеют значения

(4.1)

т. е. генератор считается симметричным с прямым чередованием фаз.

При соединении нагрузок треугольником фазные напряжения будут равны линейным, а линейные токи равны геометрической разности двух фазных токов, подходящих к вершине треугольника нагрузок, как показано на рис. 4.6. При этом для положительных направлений токов справедливы следующие соотношения, которые устанавливают связь между линейными и фазными токами

(4.2)

Фазные токи рассчитываются по известным линейным напряжениям и проводимостям Y_AB, Y_BC, Y_CA фаз приемников

(4.3)

Если падения напряжений на проводах линий передачи малы, то можно считать, что напряжения генератора равны соответствующим напряжениям приемника, т. е. .

Из уравнений (26.2) также следует, что при любых значениях фазных токов для линейных токов справедливо выражение

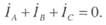(4.4)

Следует отметить, что включение нагрузок по схеме треугольника возможно при любом включении обмоток генератора, как по схеме треугольника, так и по схеме звезды. Однако, при включении генератора по схеме звезды фазные напряжения приемника будут равны линейным напряжениям генератора. При этом нулевая точка генератора не используется.

Рассмотрим некоторые частные режимы работы при включении нагрузок по схеме треугольника. К таким режимам относятся:

□ равномерная нагрузка фаз генератора;

□ неравномерная нагрузка фаз генератора;

□ обрыв одной фазы приемника;

□ обрыв двух фаз приемника;

□ обрыв линейного провода.

Короткое замыкание любой фазы приемника приводит к аварийному режиму, так как при этом замыкается накоротко одна из обмоток генератора, и поэтому недопустимо.

Рисунок 4.5

Рисунок 4.6

Равномерная нагрузка фаз генератора. При симметричной системе напряжений генератора, определяемых уравнениями (4.1) и одинаковой нагрузке фаз приемника (Y_AB = Y_BC = Y_CA = Y_n) действующие значения токов в фазах равны между собой, поэтому линейные токи связаны с фазными токами соотношением

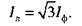(4.5)

Токи в фазах приемника определяются по формулам (4.3) и при равенстве проводимостей имеют значения

Векторная диаграмма для равномерной нагрузки фаз генератора приведена на рис. 4.7 а.

Неравномерная нагрузка фаз генератора. Неравномерная нагрузка фаз генератора является наиболее распространенным режимом работы трехфазной системы. Неравномерная нагрузка характеризуется различными значениями проводимостей, включенных в приемнике, т. е. Y_AB = Y_BC = Y_CA. Действующие значения токов в фазах приемника при неравномерной нагрузке и симметричном генераторе про­порциональны проводимостям нагрузки и определяются по формулам (26.3).

Векторная диаграмма для неравномерной нагрузки фаз генератора приве­дена на рис. 4.7 б. Линейные токи при неравномерной нагрузке фаз можно определить по формулам (4.2).

Обрыв одной фазы приемника. При обрыве одной фазы приемника ток в ней будет равен нулю. Токи в других фазах приемника не изменятся, так как не изменятся фазные напряжения.

В линейном проводе, не связанном с оборванной фазой, ток также не изменится. Линейные токи двух других фаз станут равными фазным токам.

Например, при обрыве фазы А-В приемника ток I_AВ = 0, а токи других фаз не изменятся. Линейные токи в этом случае будут иметь следующие значения

. (4.7)

Векторная диаграмма обрыва фазы А-В приведена на рис. 4.7, в.

Обрыв двух фаз приемника. При обрыве двух фаз приемника ток в них будет равен нулю. Ток в неповрежденной фазе не изменится, так как напряже­ние на ней сохранится неизменным.

Ток в линейном проводе, подходящем к оборванным фазам, будет равен нулю. Токи в других линейных проводах станут равны фазным токам.

Так, например, при обрыве фаз А-В и В-С фазные токи I_АВ = I_BC = 0, а линейные токи примут значения

(4.8)

Векторная диаграмма токов и напряжений при обрыве двух фаз приемник приведена на рис. 4.7, г.

Обрыв линейного провода. При обрыве линейного провода трехфазная система превращается в однофазную. При этом напряжение и ток в фазе, не связанной с оборванным линейным проводом, останутся без изменений.

Две другие фазы, связанные с оборванным линейным проводом, оказываются соединенными последовательно и подключенными параллельно первой фазе.

Так, например, при обрыве линейного провода А фазы А-В и В-С будут включены последовательно и подключены параллельно фазе В-С, напряжение на которой равно U_BC.

Токи в фазах определяются уравнениями

Векторная диаграмма токов и напряжений при обрыве линейного провода приведена на рис. 4.7, д.

Трехфазная система звезда - треугольник. Выше было сказано, что способ соединения обмоток генератора не предопределяет способ соединения нагрузок. Поэтому на практике к трехфазному генератору, включенному по схеме звезды, можно подключить нагрузку, соединенную по схеме треугольника. Схема подобного подключения приведена на рис. 4.8.

Рисунок 4.7

Рисунок 4.8

Из этой схемы следует, что каждое плечо треугольника оказывается включенным на линейное напряжение генератора; соединенного по схеме звезды. Поскольку линейное напряжение в 3 раза больше фазного, то токи в фазах симметричного приемника также вырастут в 3 раза. В общем случае их можно определить по формулам

(4.9)

При расчете от системы звезда-треугольник можно перейти к системе звезда-звезда. При таком преобразовании можно использовать эквивалентность схем звезды и треугольника, при которой сохраняются все напряжения и токи на внешних зажимах этих схем. Такое преобразование приводит в общем случае к эквивалентным сопротивлениям схемы звезды

(4.10)

Из уравнений (4.10) получим, что для симметричного треугольника с проводимостями Y_Δ можно найти сопротивления эквивалентной звезды

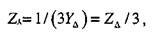(4.11)

откуда следует, что сопротивления эквивалентной звезды для симметричной схемы в три раза меньше сопротивлений треугольника.

Следует отметить, что хотя в результате такого преобразования получается система звезда-звезда, ввести в нее нулевой провод нельзя, так как в реальной схеме этого соединения нет и при введении нулевого провода получается схема, отличная от исходной.

Пример 2. Требуется определить линейные токи в нагрузке, соединенной треугольником, которая подключена к симметричному трехфазному генератору с линейным напряжением Е_л = 220 В. Сопротивления фаз приемника имеют значения: Z_AB = Z_BC = 50 Ом, Z_CA = (30 + j40) Ом. Схема соединений генератора t нагрузкой приведена на рис. 4.9, а.

Решение. Приемник с такими нагрузками относится к разряду схем с неравномерной нагрузкой фаз генератора. Для определения линейных токов в такой схеме можно воспользоваться уравнениями (4.2), в которые входят фазные токи, определяемые по уравнениям (4.3). В связи с этим, определим вначале фазные токи, пользуясь уравнениями (4.3)

Далее с помощью формул (4.2) определим линейные токи

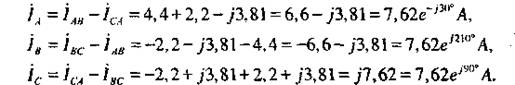
Сумма линейных токов в цепи

что подтверждает корректность решения. Векторная диаграмма токов и напряжений в схеме приведена на рис. 4.9 б.