Лабораторная работа №7.
Исследование последовательного включения активного сопротивления, индуктивности и емкости в цепи переменного тока.
Цель работы: Провести экспериментальное исследование последовательной RLC цепи. Пронаблюдать явление резонанса напряжений в последовательном колебательном контуре.
Теоретические сведения.
Рассмотрим последовательное соединение катушки, обладающей индуктивным 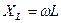 и активным
и активным 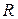 сопротивлениями, и конденсатора, обладающего емкостным сопротивлением
сопротивлениями, и конденсатора, обладающего емкостным сопротивлением 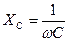 (рис. 1). При подключении такой цепи к напряжению
(рис. 1). При подключении такой цепи к напряжению 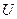 в ней возникает ток
в ней возникает ток  .
.
Вектор активного напряжения 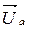 , где
, где 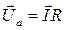 будет совпадать по направлениюс вектором тока
будет совпадать по направлениюс вектором тока 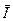 (рис. 1), так как на активном сопротивлении ток и напряжение совпадают по фазе
(рис. 1), так как на активном сопротивлении ток и напряжение совпадают по фазе
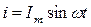 и
и 

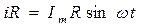
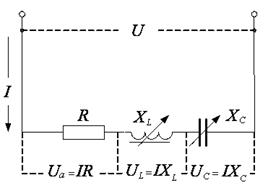
Рис. 1. Электрическая цепь из последовательно включенных активного сопротивления, катушки индуктивности и конденсатора.
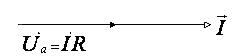
Рис. 2. Векторная диаграмма тока и напряжения через активное сопротивление.
Вектор индуктивного напряжения 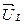 опережает вектор тока
опережает вектор тока 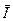 на
на 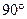 (рис. 3)
(рис. 3)
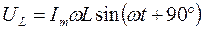
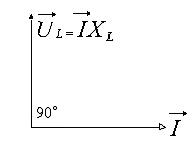
Рис. 3. Векторная диаграмма тока и напряжения при индуктивной нагрузке цепи.
Вектор емкостного напряжения 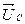 отстает от вектора тока
отстает от вектора тока 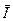 на
на 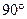 (рис.4)
(рис.4)
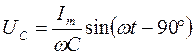
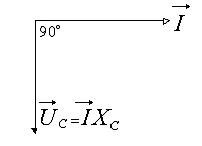
Рис.4. Векторная диаграмма тока и напряжения при емкостной нагрузке цепи.
Для рассматриваемой цепи уравнение второго закона Кирхгофа имеет вид:
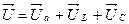 , ,
| ||
где 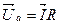 ; ; 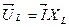 ; ; 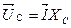 . .
|
Векторная диаграмма напряжений цепи (рис. 3) будет иметь вид, показанный на рис. 5, где вектор 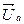 совпадает с вектором
совпадает с вектором 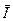 , а вектор
, а вектор 
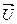 L опережает на
L опережает на 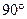 вектор
вектор 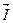 . Сумма векторов
. Сумма векторов 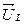 и
и 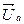 дает вектор напряжения катушки
дает вектор напряжения катушки
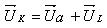 ,
,
опережающий ток на угол 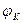 .
.
Вектор 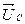 отстает на
отстает на 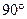 от вектора
от вектора 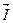 .
.
Сумма векторов 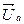 ,
, 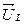 , и
, и 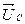 дает вектор напряжения сети
дает вектор напряжения сети 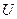 , опережающий ток на угол
, опережающий ток на угол 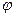 .
.
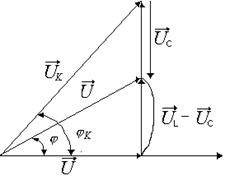
Рис. 5. Векторная диаграмма 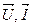 для цепи с последовательным соединением
для цепи с последовательным соединением
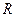 ,
, 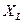 ,
, 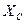 при
при 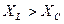
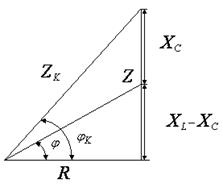
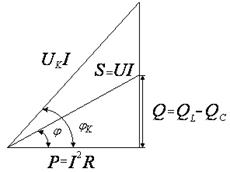
Разделив или умножив стороны треугольника (рис.5) на величину тока  , получим треугольник сопротивлений (рис. 6) или треугольник мощностей (рис. 7)
, получим треугольник сопротивлений (рис. 6) или треугольник мощностей (рис. 7)
.
| 
|
Рис. 6. Треугольник сопротивлений для цепи с последовательным соединением
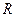 , , 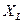 , , 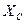
| Рис. 7. Треугольник мощностей для цепи с последовательным соединением
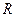 , , 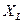 , , 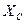
|
Из треугольника сопротивлений (рис. 7) найдем полное сопротивление 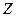 и
и 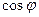 цепи:
цепи:
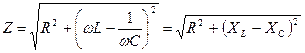
| (5) | |
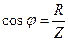
| (6) |
Из векторной диаграммы напряжений (рис. 6) получим формулу тока  , которая является выражением закона Ома для последовательных цепей переменного тока:
, которая является выражением закона Ома для последовательных цепей переменного тока:
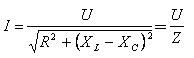
| (7) |
Из диаграммы мощностей (рис. 8) получим соотношение между полной 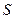 , активной
, активной 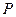 и реактивными
и реактивными 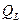 и
и 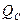 мощностями:
мощностями:
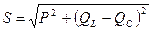
| (8) |
Изменяя величину индуктивности 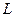 цепи, можно изменять соотношение между емкостным и индуктивным сопротивлениями и напряжениями
цепи, можно изменять соотношение между емкостным и индуктивным сопротивлениями и напряжениями 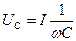 и
и 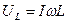 и получать различные значения угла
и получать различные значения угла 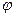 , так что вектор тока
, так что вектор тока 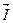 может опережать или отставать от вектора напряжения сети
может опережать или отставать от вектора напряжения сети 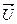 .
.
Если величина 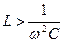 , то:
, то:
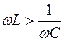 и
и 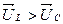
Так как преобладает индуктивное сопротивление 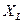 и напряжение
и напряжение 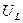 , то вектор тока
, то вектор тока 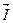 отстает от вектора напряжения сети
отстает от вектора напряжения сети 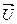 (рис. 6).
(рис. 6).
Если 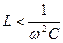 , тогда преобладает емкостное сопротивление
, тогда преобладает емкостное сопротивление 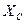 и напряжение
и напряжение 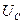 :
: 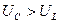 , поэтому вектор тока
, поэтому вектор тока 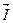 опережает вектор напряжения сети
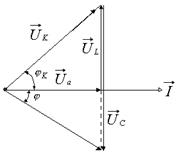
опережает вектор напряжения сети 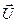 (рис. 8).
(рис. 8).
| 
|
Рис.8. Векторная диаграмма  , , 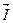 для цепи с последовательным соединением для цепи с последовательным соединением 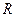 , , 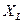 , , 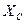 при при 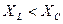
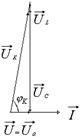
| Рис. 9. Векторная диаграмма 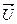 , , 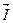 при резонансе напряжений ( при резонансе напряжений (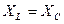 ) )
|
При выполнении соотношения
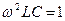
| (9) |
индуктивное сопротивление будет равно емкостному:
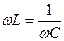 ; ; 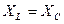
| (10) |
и, следовательно, индуктивное и емкостное напряжения равны между собой (рис. 10)
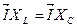 ; ; 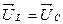 . .
| (11) |
Получим резонанс напряжений, т.е. полную взаимную компенсацию индуктивного и емкостного напряжений:
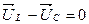 .
.
При резонансе напряжений угол 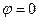 , следовательно,
, следовательно,
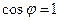
| (12) |
Вектор 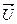 совпадает с вектором
совпадает с вектором 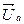 (рис. 9). Полное сопротивление цепи при резонансе
(рис. 9). Полное сопротивление цепи при резонансе 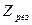 принимает минимальное значение
принимает минимальное значение 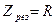 , так как
, так как 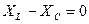 (5), а следовательно, ток при резонансе
(5), а следовательно, ток при резонансе 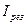 и активная мощность
и активная мощность 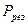 принимают максимальные значения:
принимают максимальные значения:
 ; ; 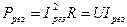
| (13) |
Реактивная мощность равна нулю:
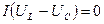 ; ; 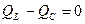
| (14) |
Индуктивное 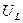 и емкостное
и емкостное 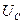 напряжения в
напряжения в 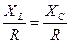 раз больше напряжения
раз больше напряжения
сети 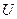 . Поэтому резонанс напряжений может оказаться опасным для установки, в которой он имеет место.
. Поэтому резонанс напряжений может оказаться опасным для установки, в которой он имеет место.
Явление резонанса напряжений, т.е. взаимной компенсации реактивных напряжений 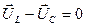 , а, следовательно, и реактивных мощностей
, а, следовательно, и реактивных мощностей 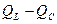 объясняется тем, что мгновенные значения напряжений на индуктивности
объясняется тем, что мгновенные значения напряжений на индуктивности 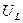 и на емкости
и на емкости 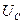 в любой момент времени равны и имеют противоположные знаки. Отсюда следует, что если, например, индуктивность берет энергию из сети для создания магнитного поля, то в этот момент конденсатор, разряжаясь, отдает энергию в сеть. Происходит взаимная компенсация энергии, потребляемой ими из сети.
в любой момент времени равны и имеют противоположные знаки. Отсюда следует, что если, например, индуктивность берет энергию из сети для создания магнитного поля, то в этот момент конденсатор, разряжаясь, отдает энергию в сеть. Происходит взаимная компенсация энергии, потребляемой ими из сети.
Таким образом, при резонансе общая энергия, потребляемая из сети, расходуется только на нагревание активного сопротивления цепи.
Кривая зависимости полного сопротивления 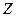 цепи от величины емкости
цепи от величины емкости 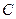 показана на рис. 10. При
показана на рис. 10. При 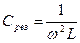
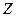 принимает минимальное значение
принимает минимальное значение 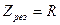 .
.
При 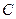 больше или меньше
больше или меньше 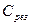 на рис. 11 показаны также кривые зависимости тока
на рис. 11 показаны также кривые зависимости тока  и
и 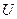 от величины
от величины 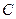 .
.
При 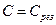 ток
ток  имеет максимальное значение:
имеет максимальное значение: 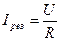 ;
;
при всех других значениях С: 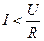 .
.
Из выражения (9) видно, что величина емкости и индуктивности, при которых возникает явление резонанса, зависят от частоты тока. При заданных постоянных 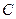 и
и 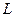 явление резонанса может быть получено изменением частоты.
явление резонанса может быть получено изменением частоты.
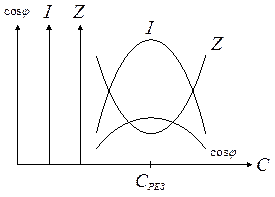
|
Рис. 10. График зависимости полного сопротивления цепи 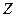 , тока , тока 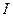 и коэффициента мощности и коэффициента мощности 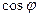 от емкости от емкости  . .
|
Выполнение работы.
Проводится исследование электрической цепи с последовательно включенными сопротивлением, емкостью и индуктивностью. Исследование включает расчет основных параметров RLC цепи, сборку электрической схемы, измерение тока и напряжений на элементах цепи. Схема последовательной цепи изображена на рис.11.
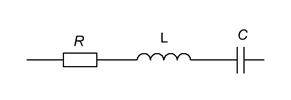
Рис.11 Последовательная RLC цепь.
Задание 1. Измерение напряжения и тока на элементах последовательной RLC цепи.
1. Заполнить Таблицу 1 для вашего варианта значения RLC –элементов (вариант выдается преподавателем). По формулам вычислить индуктивное, емкостное и полное сопротивления цепи, а также резонансную частоту контура. Частота источника переменного напряжения fист. также выдается преподавателем.
Расчетные формулы:
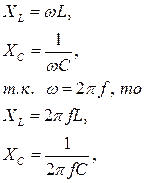
Полное сопротивление катушки индуктивности определяется по формуле
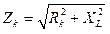 ,
,
где Rk – активное сопротивление катушки индуктивности, измеряется омметром;
Полное сопротивление последовательной RLC цепи
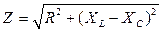
здесь f – частота источника переменного напряжения fист.
Собственная резонансная частота колебательного контура определяется выражением
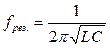 .
.
Во всех представленных выше формулах используются следующие единицы измерения: R, Rk ХL, ХC, Zk, Z в измеряется Ом, С в Ф, f в Гц.
Определить угол сдвига фаз, используя треугольник сопротивлений.
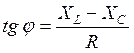
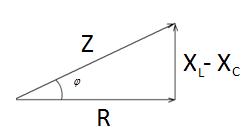
Таблица 1.
| Измеренные (номинальные) значения | Расчетные значения | |||||||||
| R, Ом | Rk, Ом | L, Гн | С, Ф | fист, Гц | fрез, Гц | ХL, Ом | ХС, Ом | Zk, Ом | Z, Ом | |