Подстановка одной функции в другую

Негосударственное образовательное учреждение высшего профессионального образования

«РОССИЙСКИЙ НОВЫЙ УНИВЕРСИТЕТ»

Воскресенский филиал

Кафедра прикладной информатики и естественнонаучных дисциплин

 

 

Контрольная работа

По теории алгоритмов

 

IV-вариант

 

 

Выполнил:

студента 2 курса на базе среднего профессионального (профильного) образования заочной формы обучения группы ИП11 Макарова Юрий Игоревич

 

Проверил:

старший преподаватель

Березенцева Т.Н.

 

Воскресенск

2013 г.

1. Определить, какая функция получается при суперпозиции функции g(x)=x+1 с самой собой.

h(x)= g(g(х))=x+2

Ответ: Суперпозиция функции g(х) с самой собой получим функцию h(х) = х + 2.

2. Определить, какая функция возникает примитивной рекурсией из функций g= x и h=x^z.

f(0)=g(0)=0;

f(1)=h(0, g(0))=0⁰=0;

f(2)=h(1, f(1))=1⁰=1;

f(3)=h(2, f(2))=2¹=2;

f(4)=h(3, f(3))=3²=9;

…

f(x)=(x-1)^(x-2)

Ответ: Примитивная рекурсией из функций g= x и h=x^z есть функция f(x)=(x-1)^(x-2)

3. Покажите, что функция f(x,y)= 2x+3y является примитивно рекурсивной.

Доказательство.

Функция f(x; y) удовлетворяет соотношениям: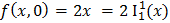

f(x; y + 1) =2 x + 3(y + 1) = 2x + 3y + 3 = s(s(s(2x + 3y))) = s(s(s(f(x; y)))):

Следовательно, функция f(x; y) возникает из примитивно рекурсивных функци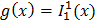й

и 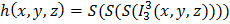операцией примитивной рекурсии и поэтому функция f(x; y) = 2x + 3y является примитивно рекурсивной.

Доказано.

4. Доказано. Постройте программу машины Тьюринга, вычисляющую функцию f(x)=x-3

↓

Пусть внешним алфавитом данной МТ является множество A = {0,1}. Число x на ленте машины записывать в виде набора из x единиц:

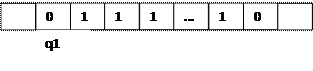Программа МТ выглядит следующим образом:

q₁1→1Пq₁;… q₁0→0Лq₁; q₁0→0Лq₁; q₁0→0Лq₀.

согласно которой для любой начальной конфигурации, когда считывающая головка обозревает одну из единиц, в каждый момент эта единица остается на месте, и головка сдвигается вправо на одну ячейку. Этот процесс продолжается до тех пор, пока головка не выйдет на пустую ячейку. Тогда в головка смещается влево и записывает 0, производит еще 2 такие операции. Машина перейдет в состояние q₀.

Стоит учесть, что если вводные данные меньше трех машина зацикливается и переходит в состояние q₀.

5. Суперпозиция (сложная функция) — это функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных.

Способы получения суперпозиций Рассмотрим две булевы функции: функцию 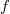от 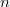аргументов 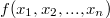и функцию 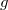от 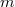аргументов .
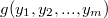Тогда мы можем получить новую функцию из имеющихся двумя способами:

· Подстановкой одной функции в качестве некоторого аргумента для другой;

· Отождествлением аргументов функций.

Подстановка одной функции в другую

Подстановкой функции g в функцию f называется замена i-того аргумента функции f значением функции g:

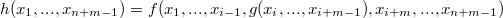
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.

При подстановке функции 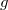вместо 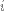-того аргумента функции 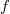, результирующая функция 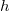будет принимать аргументы, которые можно разделить на следующие блоки:

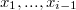
1.	— аргументы 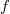функции до подставленного значения функции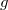
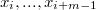
2.	— используются как аргументы для вычисления значения функции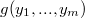
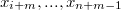
3.	— аргументы функции 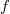после подставленного значения функции g

Отождествлением переменных называется подстановка 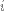-того аргумента функции 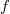вместо 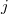-того аргумента:

 

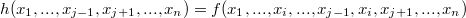
Таким образом, при отождествлении переменных мы получаем функцию 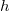с количеством аргументов .

 

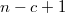Пример машины Тьюринга

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_jзаписывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины

Приведу пример МТ для умножения чисел в унарной системе счисления. Машина работает по следующему набору правил:

Набор правил	Набор правил
q0*→q0*R	q4a→q4aR
q01→q01R	q4=→q4=R
q0×→q1×R	q41→q41R
q11→q2aR	q4*→q51R
q21→q21L	q5 →q2*L
q2a→q2aL	q6a→q61R
q2=→q2=L	q6×→q7×R
q2×→q3×L	q7a→q7aR
q31 → q4aR	q71→q2aR
q3a→q3aL	q7=→q8=L
q3*→q6*R	q8a→q81L
q4×→q4×R	q8×→q9×N

 

Умножим с помощью МТ 3 на 2 в единичной системе: