Решение задач линейной оптимизации в Ms Excel с помощью надстройки «Поиск решения»
Цель работы:
1. Уметь составлять математическую (формальную) модель задачи в виде системы линейных алгебраических уравнений.
2. Научиться решать линейные оптимизационные задачи с помощью надстройки Ms Excel «Поиск решения».
Задание:
Для 3-х задач создать их математические модели (выполнить формальную постановку задачи) и с помощью надстройки Excel «Поиск решения» вычислить их целевые функции.
Ход работы:
Задача 1
Для изготовления трёх видов изделий используется четыре вида оборудования. Затраты времени на обработку одного изделия на каждом виде оборудования, общий фонд рабочего времени оборудования и прибыль от продажи единицы изделия приведены в таблице:
| Тип оборудования | Затраты времени на обработку одного изделия | Общий фонд рабочего времени оборудования | ||
| I | II | III | ||
| I | ||||
| II | ||||
| III | ||||
| IV | ||||
| Прибыль |
Требуется определить, сколько изделий и какого вида следует изготовить, чтобы получить максимальную прибыль от их продажи.
Обозначим через
x1 - количество изготовленных изделий I вида,
x2 - количество изготовленных изделий II вида,
x3 - количество изготовленных изделий III вида.
Тогда, учитывая общий фонд рабочего времени оборудования, получим систему неравенств:
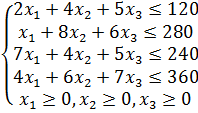
Целевая функция:

Теперь подробно отразим порядок действий при работе с надстройкой Ms Excel «Поиск решения»:
1. Выставим ограничения для задачи, согласно системе неравенств, а также определим целевую функцию.
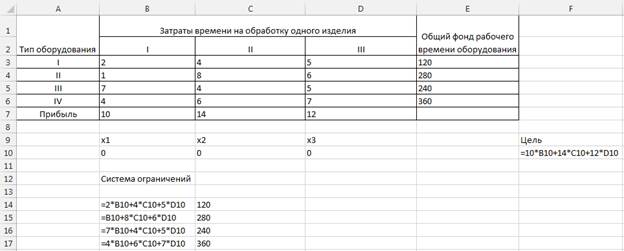
Рисунок 4 – Система ограничений и целевая функция.
2. Далее нажимаем на «Данные – Поиск решения».
3. В поле «Оптимизировать целевую функцию» указываем клетку с целевой функцией.

Рисунок 5 – Оптимизация целевой функции.
4. Указываем, что следует искать максимальное значение целевой функции.

Рисунок 6 – Выбор максимального значения функции.
5. Далее обозначаем какие ячейки переменных мы используем.

Рисунок 7 – Ячейки переменных.
6. Затем прописываем все ограничения, в соответствии с системой неравенств.

Рисунок 8 – Ограничения.
7. В результате, окно «Параметры поиска решения» выглядит следующим образом.

Рисунок 9 – Параметры поиска решения.
8. После нажатия на кнопку «Поиск решения» мы получаем следующий результат:
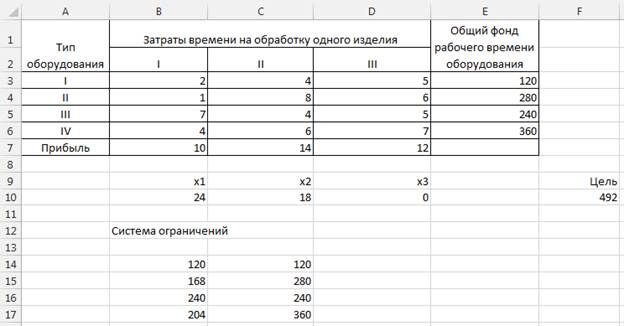
Рисунок 10 – Результаты вычислений.
Задача 2
Молочный завод производит молоко, кефир и сметану. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. Затраты рабочего времени на разлив 1 т молока, сметаны и кефира составляют соответственно 0,18, 0,19 и 3,25 часов. Общий объём используемого молока заводом в сутки не превышает 136000 кг. Оборудование, используемое для разлива молока и кефира, может работать в сутки не более 21,4 часа, а сметаны – не более 16,25 часа. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 3000, 2200 и 1360 рублей. Завод должен производить не менее 100 т молока.
Определить план выпуска заводом молочной продукции, который обеспечивает заводу максимальную ежедневную прибыль.
Оформим исходные данные в виде таблицы:
| Тип продукции | Затраты молока | Затраты времени | Общий объем используемого молока | Лимит работы оборудования для розлива | Прибыль |
| Молоко | 0,18 | 21,4 | |||
| Кефир | 3,25 | ||||
| Сметана | 0,19 | 16,25 |
Обозначим через
x1 – количество тонн, произведенного молока,
x2 – количество тонн, произведенного кефира,
x3 – количество тонн, произведенной сметаны.
Система неравенств:
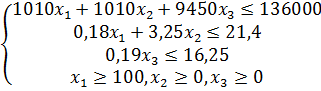
Целевая функция:

Теперь, с помощью Ms Excel найдем решение этой задачи:
1. Выставим ограничения для задачи, согласно системе неравенств, а также определим целевую функцию.

Рисунок 11 - Система ограничений и целевая функция.
2. Занесем наши данные в параметры поиска решения.

Рисунок 12 – Параметры поиска решения.
3. После нажатия на кнопку «Поиск решения» мы получаем следующий результат:
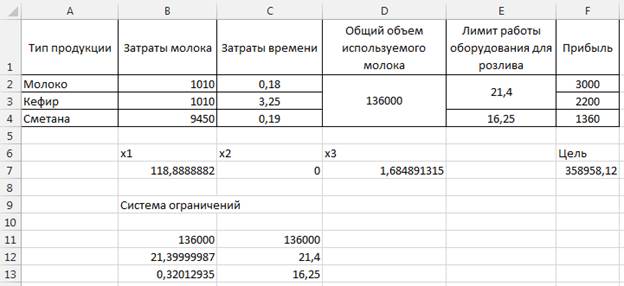
Рисунок 13 – Результаты вычислений.
Задача 3
Фирма «Фасад» производит двери для продажи местным строительным компаниям. Репутация фирмы позволяет ей продавать всю производимую продукцию. На фирме работает 10 рабочих в одну смену (8 рабочих часов), 5 дней в неделю, что дает 400 часов в неделю. Рабочее время поделено между двумя существенно различными технологическими процессами: собственно производством и конечной обработкой дверей. Из 400 рабочих часов в неделю 250 отведены под собственно производство и 150 под конечную обработку. «Фасад» производит 3 типа дверей: стандартные, полированные и резные. В таблице приведены временные затраты и прибыль от продажи одной двери каждого типа.
| Время на производство (мин) | Время на обработку (мин) | Прибыль | |
| Стандартные | $45 | ||
| Полированные | $90 | ||
| Резные | $120 |
a. Сколько дверей различных типов нужно производить, чтобы максимизировать прибыль?
b. Оптимально ли распределение рабочего времени между двумя технологическими процессами (производство и конечная обработка)? Как изменится прибыль, если распределить рабочее время между этими процессами оптимально?
Обозначим через
x1 – количество произведенных стандартных дверей,
x2 – количество произведенных полированных дверей,
x3 – количество произведенных резных дверей.
Система неравенств:

Целевая функция:

Теперь, с помощью Ms Excel найдем решение этой задачи:
Задание a
1. Выставим ограничения для задачи, согласно системе неравенств, а также определим целевую функцию.

Рисунок 14 - Система ограничений и целевая функция.
2. Занесем наши данные в параметры поиска решения.

Рисунок 15 - Параметры поиска решения.
3. После нажатия на кнопку «Поиск решения» мы получаем следующий результат:

Рисунок 16 - Результаты вычислений.
Задание b
1. Выставим ограничения для задачи, согласно системе неравенств, а также определим целевую функцию.

Рисунок 17 - Система ограничений и целевая функция.
2. Занесем наши данные в параметры поиска решения.

Рисунок 18 - Параметры поиска решения.
3. После нажатия на кнопку «Поиск решения» мы получаем следующий результат:

Рисунок 19 - Результаты вычислений.
Вывод:
Научился составлять математическую (формальную) модель задачи в виде системы линейных алгебраических уравнений, а также решать линейные оптимизационные задачи с помощью надстройки Ms Excel «Поиск решения».
Лабораторная работа №3
Введение в сетевой анализ. Методы и инструменты сетевого планирования и составления расписания проекта
Цель работы:
1. Иметь представление о сетевом анализе и применяемых методиках.
2. Знать детерминированные и вероятностные методы и инструменты сетевого планирования и составления расписания проекта, их особенности, области применения, достоинства и недостатки.
Задание:
Составить теоретический отчёт о методах и инструментах сетевого планирования (анализа).
Краткие теоретические сведения:
1. Сетевое планирование (сетевой анализ, составление расписания проекта)
Понятие
Сетевой анализ (сетевое планирование) — метод анализа сроков (ранних и поздних) начала и окончания нереализованных частей проекта, позволяет увязать выполнение различных работ и процессов во времени, получив прогноз общей продолжительности реализации всего проекта.
1.2 Методы сетевого планирования (классификация): детерминированные и вероятностные
· Детерминированные сетевые методы
o Диаграмма Ганта с дополнительным временным люфтом 10-20 %
o Метод критического пути (МКП)
· Вероятностные сетевые методы
o Неальтернативные
§ Метод статистических испытаний (метод Монте-Карло)
§ Метод оценки и пересмотра планов (ПЕРТ, PERT)
o Альтернативные
§ Метод графической оценки и анализа (GERT)
2. Методы и инструменты сетевого планирования (обзор, графическое отображение (пример построения), достоинства и недостатки)
Детерминированные методы и инструменты
2.1.1 Иерархическая структура работ (WBS)
Иерархическая структура работ (ИСР) (англ. Work Breakdown Structure, WBS; иногда Структура декомпозиции работ, СДР) — это иерархическое разбиение всей работы, которую необходимо выполнить для достижения целей проекта, на более мелкие операции и действия до такого уровня, на котором способы выполнения этих действий вполне ясны и соответствующие работы могут быть оценены и спланированы. Она включает также определение промежуточных результатов всех составляющих эту структуру работ.
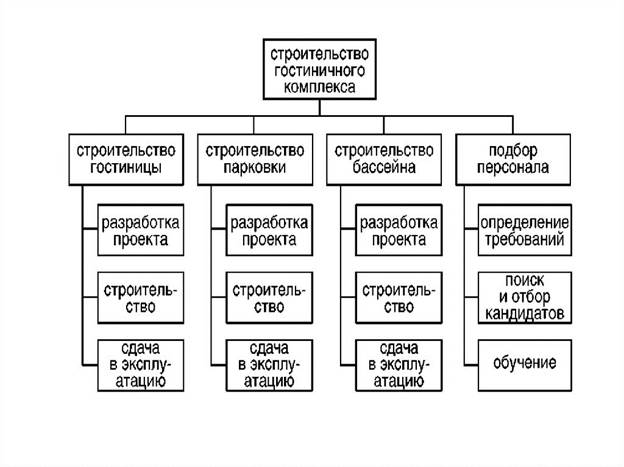
Рисунок 20 – Пример иерархической структуры.
Преимущества иерархической структуры:
· четкая система взаимных связей функций и подразделений;
· четкая система единоначалия - один руководитель сосредотачивает в своих руках руководство всей совокупностью процессов, имеющих общую цель;
· ясно выраженная ответственность;
· быстрая реакция исполнительных подразделений на прямые указания вышестоящих.
Недостатки иерархической структуры:
· отсутствие звеньев, занимающихся вопросами стратегического планирования; в работе руководителей практически всех уровней оперативные проблемы ("текучка") доминирует над стратегическими;
· тенденция к волоките и перекладыванию ответственности при решении проблем, требующих участия нескольких подразделений;
· малая гибкость и приспособляемость к изменению ситуации;
· критерии эффективности и качества работы подразделений и организации в целом - разные;
· перегрузка управленцев верхнего уровня;
· повышенная зависимость результатов работы организации от квалификации, личных и деловых качеств высших управленцев.
2.1.2 Сетевой график (граф)
Сетевой график — это динамическая модель производственного процесса, отражающая технологическую зависимость и последовательность выполнения комплекса работ, связывающая их свершение во времени с учётом затрат ресурсов и стоимости работ с выделением при этом узких (критических) мест.

Рисунок 21 – Пример сетевого графика.
Достоинства сетевого графика:
· Наиболее полная взаимосвязь между работами при определенной технологической последовательности; акцентирование внимания руководителей на работах, от которых зависит срок выполнения всей программы
· Максимальное сокращение влияния случайных или «волевых» факторов с возможностью анализа вариантов и выбора оптимального
· Осуществление четкого контроля за ходом выполнения работ и предотвращение нарушения плановых сроков
· Возможность применения ЭВМ для расчетов параметров сетевой модели
Главный недостаток сетевого планирования – его строгая линейность, инвариантность действий и последовательности их осуществления. В сетевом плане не находят отражения вариативные действия и альтернативные способы их осуществления. Если какое-либо действие введено в план с ошибкой в сроках, способах исполнения или ресурсах, то прерывается вся цепочка действий, и процесс требует существенных корректив. Кроме того, сетевое планирование плохо отражает параллельно протекающие действия.
2.1.3 Метод критического пути (CPM)
Метод критического пути (англ. CPM, Critical path method) — инструмент планирования расписания и управления сроками проекта.
В основе метода лежит определение наиболее длительной последовательности задач от начала проекта до его окончания с учетом их взаимосвязи. Задачи, лежащие на критическом пути (критические задачи), имеют нулевой резерв времени выполнения, и, в случае изменения их длительности, изменяются сроки всего проекта. В связи с этим, при выполнении проекта критические задачи требуют более тщательного контроля, в частности, своевременного выявления проблем и рисков, влияющих на сроки их выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе выполнения проекта критический путь проекта может меняться, так как при изменении длительности задач некоторые из них могут оказаться на критическом пути.

Рисунок 22 – Пример метода критического пути.
Ключевые преимущества метода:
1) Определение ключевых (критичных) задач становится легче, наглядно отображается их влияние на жизнь проекта.
2) Управление временем проекта — оптимизация временных затрат благодаря пониманию затраченных ресурсов на каждую задачу.
3) Возможность быстрого реагирования на внеплановые изменения.
4) Сравнение фактического результата с запланированным — если каждую неделю обновлять критический путь, то к окончанию разработки продукта будет видно, насколько планы отличаются от реальности.
5) Показывает четкие зависимости одних задач от других.
6) Концентрация — само планирование расписания проекта подразумевает сосредоточенность на каждой из критично важных задач и на конечном результате одновременно.
Недостатки метода критического пути:
1) Увеличение срока создания продукта — за счет обязательного резерва времени у критических задач.
2) Часто задача занимает всё время, отведенное на нее (классический закон Паркинсона в действии).
3) Окончание одной задачи раньше далеко не всегда приводит к раннему окончанию создания всего продукта из-за жестких сроков и распределения ресурсов. Так сказать, один бой не решает войну.
4) Сложность применения методики в решении творческих задач — как прогнозировать сроки проекта из-за огромного количества нестабильных переменных?
5) Сложность применения в проектах с повышенными рисками выполнения.
2.1.4 Диаграмма Гантта (Ганта)
Диагра́мма Га́нтта (англ. Gantt chart, также ленточная диаграмма, график Гантта, календарный график) — это популярный тип столбчатых диаграмм (гистограмм), который используется для иллюстрации плана, графика работ по какому-либо проекту. Является одним из методов планирования проектов. Используется в приложениях по управлению проектами.
Первый формат диаграммы был разработан Генри Л. Ганттом в 1910 году.
По сути, диаграмма Гантта состоит из полос, ориентированных вдоль оси времени. Каждая полоса на диаграмме представляет отдельную задачу в составе проекта (вид работы), её концы — моменты начала и завершения работы, её протяженность — длительность работы. Вертикальной осью диаграммы служит перечень задач. Кроме того, на диаграмме могут быть отмечены совокупные задачи, проценты завершения, указатели последовательности и зависимости работ, метки ключевых моментов (вехи), метка текущего момента времени «Сегодня» и др.
Ключевым понятием диаграммы Гантта является «веха» — метка значимого момента в ходе выполнения работ, общая граница двух или более задач. Вехи позволяют наглядно отобразить необходимость синхронизации, последовательности в выполнении различных работ. Вехи, как и другие границы на диаграмме, не являются календарными датами. Сдвиг вехи приводит к сдвигу всего проекта. Поэтому диаграмма Гантта не является, строго говоря, графиком работ. Кроме того, диаграмма Гантта не отображает значимости или ресурсоемкости работ, не отображает сущности работ (области действия). Для крупных проектов диаграмма Гантта становится чрезмерно тяжеловесной и теряет всякую наглядность.
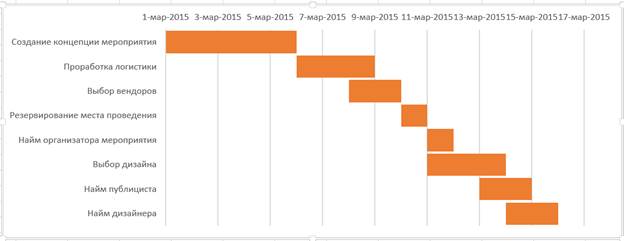
Рисунок 23 – Пример диаграммы Ганта.
Преимущества и недостатки метода:
Главным преимуществом, бесспорно, является графическая подача материала. Как правило, бизнесменам удобно работать с графиками Ганта – им нравится возможность чётко выделить и обозначить этапы работы над проектом. За счёт представления заданий в виде различных цветных полос все члены команды могут буквально с первого взгляда определить свои задачи. Следует также отметить то, что диаграммы Ганта являются отличным презентационным инструментом, который способен продемонстрировать ключевые приоритеты проекта. То есть, как только руководящие лица выделяют и распределяют каждый из имеющихся в наличии ресурсов, команда моментально узнаёт об этом и следует дальнейшим указаниям. Данное свойство графика Ганта крайне полезно для управляющих высшего звена – используя его, можно намного проще подготовить подробный, ёмкий отчёт о состоянии выполнения различных проектов.
Тем не менее, как и у любого другого метода планирования, у диаграммы Ганта есть свои недостатки. Один из них – это зависимость задач. Довольно часто в процессе презентации проектов у руководящих возникает необходимость показать, какие из указанных заданий связаны друг с другом. Но, к сожалению, сам формат диаграммы не позволяет сделать этого. Для того чтобы обойти это ограничение, управляющие прибегают к различным хитростям: например, добавляют в график специальные вертикальные линии, которые демонстрируют ключевые зависимости. Однако это лишь временное решение, не способное передать информацию в полном объёме. Ещё одним минусом графиков Ганта можно назвать их негибкость. В наши дни проекты не являются статичными – в них постоянно происходят какие-то изменения, сдвиги, учесть которые в диаграмме просто невозможно. Прежде чем приступать к построению графика, управляющим приходится просчитывать всё до мелочей, ведь при малейшем изменении оценки нужно перерисовывать «с нуля» всю диаграмму. И это не говоря уже о том, что возможность проиллюстрировать несколько разных способов планирования за один раз также отсутствует. Вне зависимости от того, зачем вам нужна диаграмма Ганта, программа (даже самая «продвинутая») не сможет отобразить значимость и ресурсоёмкость тех или иных работ, их сущность. А потому для особо масштабных проектов она используется крайне редко.
2.2 Вероятностные методы:
2.2.1 Метод критической цепи (CCPM)
Метод критической цепи (англ. critical chain project management, CCPM) — метод планирования и управления проектами, базирующийся на методе критической цепи и принципах теории ограничений, который, в дополнение к традиционной технике оценки и анализа проектов PERT, опирается на расчёты по зависимостям ресурсов, рискам, неопределённостям. В частности, в методе широко применяются буферы для снижения проектных рисков в проекте и обеспечения устойчивости построенного плана-графика проекта, визуализации «трендов проникновения в буферы» (англ. fever chart), расчёт проекта от крайнего срока завершения (а не от начала, как в классическом PERT).
Впервые метод описан в 1997 году в книге Голдратта «Критическая цепь», метод встретил широкую поддержку специалистов, так как был близок по технике классическому методу PERT (ресурсные связи фактически являлись расширением сетевой модели на ресурсы), а расчётные алгоритмы оказались достаточно просты и эффективны по быстродействию. Расчёт буферов также был прост и аналогичен методике расчёта длительности работ в некоторых расширениях метода PERT и соответствовал сложившейся практике во многих организациях.

Рисунок 24 – Пример метода критической цепи.
Преимущества метода критической цепи:
· Помогает определить ключевые задачи: во-первых, с его помощью можно легко выделить задачи, которым следует уделить особое внимание. Если выполнение какой-либо задачи на критическом пути займёт больше времени по сравнению с предусмотренным, будет начато или завершено позже, чем планировалось, то это окажет влияние на длительность всего проекта.
· Помогает сократить время: во-вторых, "если после предварительного анализа прогнозируется время завершения, то возникает интерес к завершению проекта в более короткие сроки и становится понятным, какая задача или задачи требуют сокращения длительности", — прокомментировал доктор Беннет. Когда результаты, полученные по методу критического пути, отображаются в виде линейной диаграммы, подобной диаграмме Ганта, легко увидеть участки, в которых совпадают общие временные рамки задач. Можно отобразить виды деятельности на критическом пути (они, как правило, выделяются цветом), а также длительности и последовательности задач. Это даёт новый уровень понимания временной шкалы проекта, предоставляя вам больше информации о том, длительность каких задач можно изменить, а длительность каких оставить без изменений.
· Сравнивает запланированное с реальностью: и, наконец, по словам доктора Беннета, метод критического пути можно использовать для сравнения запланированного и фактического хода выполнения. "По мере реализации проекта базовый график, разработанный на основе предварительного анализа критического пути, можно использовать для отслеживания хода выполнения расписания. В течение проекта руководитель может определять задачи, которые уже были завершены, прогнозировать длительность оставшихся для выполнения задач, а также оценивать любые планируемые изменения в будущих последовательностях и сроках задач. В результате получится обновлённое расписание, которое, при отображении рядом с первоначальными базовыми планами, станет визуальным средством сравнения запланированного и фактического хода выполнения проекта".
Недостатки метода критической цепи:
· Прежде всего, некоторый скепсис вызывает использование вероятности завершения задач в 50% при сокращении времени их исполнения в два раза. Обозначенная оценка требует интенсивной работы команды проекта и не всегда оправдывается, несмотря на приложенные усилия.
· На результат использования МКП отрицательно влияет возможность переоценки буфера. Такая вероятность появляется при использовании правила, согласно которому размер буфера определяется как половина размера критической цепи. «Преувеличенный» буфер снижает адекватность оценки состояния проекта в определённый период времени.
· МКЦ устраняет возможность использования контрольных событий проекта, что может быть причиной осложнения организации процессов поставок необходимых критических элементов со стороны внешних участников.
· Для применения МКП необходимо формирование отдельной команды проекта, что не всегда является возможным для предприятия. Члены команды должны быть задействованы только в реализации одного проекта. Это может рассматриваться как фактор снижения эффективности использования человеческих ресурсов.
· Кроме того, все члены команды, как правило, чувствуют повышенную ответственность и нагрузку, работая по проекту согласно схеме МКП. Это приводит к усталости, стрессу, раздражительности и, как следствие, возрастанию напряжения в коллективе.
2.2.2 Метод оценки и анализа проектов (PERT)
Program (Project) Evaluation and Review Technique (сокращённо PERT) — метод оценки и анализа проектов, который используется в управлении проектами.
PERT предназначен для очень масштабных, единовременных, сложных, нерутинных проектов. Метод подразумевает наличие неопределённости, давая возможность разработать рабочий график проекта без точного знания деталей и необходимого времени для всех его составляющих.
PERT был разработан главным образом для упрощения планирования на бумаге и составления графиков больших и сложных проектов. Метод в особенности нацелен на анализ времени, которое требуется для выполнения каждой отдельной задачи, а также определение минимального необходимого времени для выполнения всего проекта.
Самой популярной частью PERT является метод критического пути, опирающийся на построение сетевого графика (сетевой диаграммы PERT).
Метод был разработан в 1958 году консалтинговой фирмой «Буз, Ален и Гамильтон[en]» совместно с корпорацией «Локхид» по заказу Подразделения специальных проектов ВМС США в составе Министерства Обороны США для проекта создания ракетной системы «Поларис» (Polaris). Проект «Поларис» был ответом на кризис, наступивший после запуска Советским Союзом первого космического спутника.

Рисунок 25 – Пример метода оценки и анализа проектов.
Преимущества технологии PERT:
· С помощью диаграмм, менеджеры проектов могут оценивать и анализировать время и ресурсы, необходимые для проекта.
· Диаграммы дают возможность отслеживания и управления активами, необходимыми на любой стадии производства.
· Анализ графиков содержит данные и информацию из различных департаментов. Это помогает оптимизировать коммуникации во время хода проекта, определить ответственные стороны в рамках компании и распределить ответственность.
· Техника помогает менеджерам сделать анализ «что-если». Такой анализ выявляет возможности и неопределенные моменты, связанные с проектом и помогает свести к минимуму неприятные сюрпризы и утраты. «Что-если» также выдвигает на первый план все рискованные события и этапы, которые требуют тщательного анализа и мониторинга в ходе реализации проекта.
Недостатки PERT:
· Метод PERT требует расположения активностей во временной последовательности. Процесс анализа носит субъективный характер, именно поэтому эти схемы не могут точно оценить стоимость и время.
· Технология определяет потребности в рабочей силе и материально-техническом оснащении для видов активностей в проекте. Тем не менее, PERT — это прежде всего метод, сфокусированный на работе с временем.
· Метод требует детального исследования и изучения замечаний от многих людей.
· PERT считается достаточно дорогой техникой из-за трудоемкого характера работ.
2.2.3 Метод графической оценки и анализа (GERT)
Метод графической оценки и анализа (GERT, англ. Graphical Evaluation and Review Technique) — альтернативный вероятностный метод сетевого планирования, применяется в случаях организации работ, когда последующие задачи могут начинаться после завершения только некоторого числа из предшествующих задач, причём не все задачи, представленные на сетевой модели, должны быть выполнены для завершения проекта.
Разработан в США в 1966 году.
Основу применения метода GERT составляет использование альтернативных сетей, называемых GERT-сетями. Они позволяют более адекватно задавать сложные процессы строительного производства в тех случаях, когда затруднительно или невозможно (по объективным причинам) однозначно определить, какие именно работы и в какой последовательности должны быть выполнены для достижения цели проекта (то есть существует многовариантность реализации проекта). Расчёт GERT-сетей, моделирующих реальные процессы, чрезвычайно сложен, однако программное обеспечение для вычисления сетевых моделей такого типа в настоящее время не распространено.

Рисунок 26 – Пример метода графической оценки и анализа.
Преимущества метода:
· Допускает, что некоторые работы могут не состояться (провалиться), изменив содержание следующих за ними работ;
· Предполагает, что допускается возвращение назад (например, переконструирование, перетестирование любой работы);
· Использование стохастического описания реализации производственных процессов позволяет решать задачу нахождения математического ожидания и стандартного отклонения директивного времени на их реализацию в условиях неопределенности.
Недостатки метода:
· Расчёт GERT-сетей, моделирующих реальные процессы, чрезвычайно сложен, однако программное обеспечение для вычисления сетевых моделей такого типа в настоящее время, к сожалению, не распространено.
2.2.4 Метод статистических испытаний (Монте-Карло)
Ме́тоды Мо́нте-Ка́рло (ММК) — группа численных методов для изучения случайных процессов. Суть метода заключается в следующем: процесс моделируется при помощи генератора случайных величин. Это повторяется много раз, а потом на основе полученных случайных данных вычисляются вероятностные характеристики решаемой задачи. Например, чтобы узнать, какое в среднем будет расстояние между двумя случайными точками в круге, методом Монте-Карло, нужно взять много случайных пар точек, для каждой пары найти расстояние, а потом усреднить.
Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.
Название метода происходит от района Монте-Карло, известного своими казино.

Рисунок 27 – Пример метода статистических испытаний.
Преимущества метода:
· Не требует никаких предположений относительно регулярности за исключением квадратичной интегрированности; это может быть полезным, так как во многих случаях встречаются очень сложные функции, свойства регулярности которых просто установить;
· Обеспечивает осуществление процедуры даже в многомерном случае, когда численное интегрирование неприменимо, например с числа измерений> 10.
· Легко применяется при малых ограничений или без предварительного анализа задачи.
Метод Монте-Карло имеет и некоторые недостатки, а именно:
· Пределы погрешности точно не определены, а включают некоторую случайность;
· Статистическая погрешность приходит очень медленно;
· Необходимые таблицы случайных чисел.
Вывод:
Узнал о сетевом анализе и применяемых методиках, а также о детерминированных и вероятностных методах и инструментах сетевого планирования, составлении расписания проекта, их особенностях, области применения, достоинствах и недостатках.