ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ И ЕГО СВОЙСТВА
Решая задачу или доказывая теорему из курса стереометрии, мы пользуемся, как правило, не пространственной моделью соответствующей фигуры, а ее изображением на плоскости, чертежом, то есть, как иногда говорят, ее графической моделью. Тот, кто хочет научиться решать стереометрические задачи, должен, прежде всего, научиться правильно изображать пространственные фигуры на плоскости – на листе бумаги или на классной доске.
Чаще всего пользуются двумя методами: 1) метод параллельного проецирования; 2) метод центрального проектирования (перспектива). Второй из представленных методов более соответствует аппарату человеческого зрения, но он очень сложен и недостаточно быстр в применении.
В стереометрии изображением фигуры (оригинала) называется любая фигура, подобная параллельной проекции данной фигуры на некоторую плоскость.
Рассмотрим, какие требования должны быть предъявлены к проекционным чертежам:
1. Изображение должно быть верным, т.е. должно представлять собой фигуру, подобную параллельной проекции оригинала.
2. Изображение должно быть по возможности наглядным, т.е. должно вызывать пространственное представление о форме оригинала.
3. Изображение должно быть полным, т.е. каждая точка принадлежащая оригиналу, должна быть задана на проекционном чертеже.
4. Изображение должно быть легко выполнимым, т.е. правила построения должны быть максимально просты.
5. Изображение должно быть удобным для проведения на нем дополнительных линий.
Более подробно рассмотрим параллельное проецирование.
Пусть α – некоторая плоскость (будем называть ее плоскостью проекции), l – некоторая прямая, пересекающая плоскость α и определяющая направление проецирования. Все прямые параллельные ей называются проецирующими. Пусть А – произвольная точка, такая что Аα. Проецируем эту точку на плоскость α, т.е. проводим через эту точку прямую параллельную l, пересекающую плоскость α в точке. Назовем эту точку А′, А′ α и АА′ l. А′ проекция точки А на плоскость α. Отсюда следует, что точки, принадлежащие плоскость α, совпадают со своими проекциями на эту плоскость.
Если каждую точку геометрической фигуры Ф проецируется на плоскость α в направлении l, то множество всех точек проекции данной фигуры Ф в направлении l называют параллельной проекцией данной фигуры Ф на α в направлении l, проекцию Ф′ называют изображением фигуры Ф на плоскость α в параллельной проекции.
Свойства параллельного проецирования:
1. Проекция прямой, не параллельной направлению проецирования, есть прямая.
2. Если точка А′ принадлежит прямой l′, то проекция А этой точки принадлежит проекции l указанной прямой.
Следствие. Если прямая А′В′ не параллельна плоскости, то точкой пересечения этой прямой с плоскостью является точка пересечения прямой и ее проекции на эту плоскость.
3. Проекции параллельных прямых, не являющихся проецируемыми, параллельны.
4. Отношение отрезков одной прямой или параллельных прямых равно отношению их проекции.
5. Параллельной проекцией окружности является эллипс (или отрезок – в случае, если окружность лежит в проецирующей плоскости).
6. Любой треугольник с точностью до подобия можно рассматривать как параллельную проекцию любого данного треугольника.
Фундаментальное значение при построении изображений пространственных фигур имеет теорема Польке-Шварца: любые три отрезка, выходящие из одной точки и принадлежащие одной плоскости, могут быть приняты за параллельные проекции трех отрезков в пространстве, длины которых находятся в заданном отношении и которые составляют друг с другом заданные углы.
Из теоремы Польке-Шварца следует важный вывод: вершины произвольного четырехугольника плоскости могут служить изображением вершин тетраэдра, равного данному тетраэдру.
ПРИМЕНЕНИЕ НЕКОТОРЫХ СВОЙСТВ ПАРАЛЛЕЛЬНОЙ
ПРОЕКЦИИ ПРИ РЕШЕНИИ ЗАДАЧ.
Задание: треугольник АВС – параллельная проекция правильного треугольника:
а) построить проекцию серединного перпендикуляра к стороне АС;
б) построить проекцию перпендикуляра, проведенного из вершины С к стороне АС.
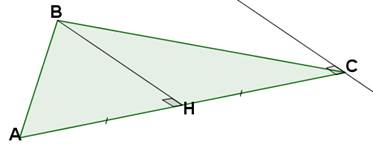
1. Строим произвольный треугольник АВС.
2. Находим середину [ АС ]: АН = НС.
3. ВН является искомым серединным перпендикуляром.
4. Проводим через точку С параллельную прямую отрезку ВН.
Задание: треугольник АВС – параллельная проекция прямоугольного треугольника. Через точку К на гипотенузе построить проекции перпендикуляров, проведенных к катетам. 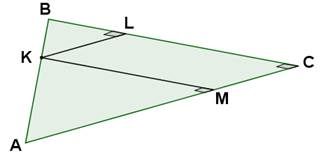
1. Строим произвольный треугольник АВС. Пусть КАВ, тогда С = 90о.
2. КМВС, М = КМАС.
3. KLВС, L= КLВС.
4. KL и KM являются искомыми перпендикулярами.
Задание: треугольник АВС – параллельная проекция прямоугольного и равнобедренного треугольника. Постройте биссектрису прямого угла.
1. Строим произвольный треугольник АВС (С = 90о, АС = СВ) 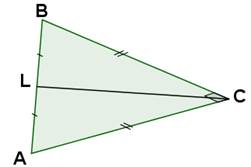
2. Находим середину [ AВ ]: AL = LB.
3. СL является искомой биссектрисой прямого угла.
Задание: в правильном тетраэдре через точку К провести перпендикуляр к AD.
1. Строим тетраэдр АВСD.
2. Находим середину [ AD ]: AE = ED. 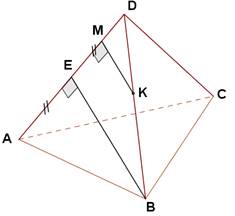
3. КМВЕ, М = КМAD.
4. КМ является искомым перпендикуляром.
Задание: параллелограмм есть изображение квадрата. Построить проекцию перпендикуляра, проведенного из точки пересечения диагоналей к стороне АВ. 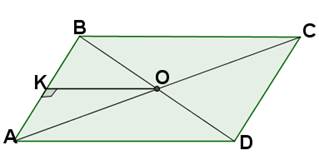
1. Строим параллелограмм АВСD.
2. Проводим диагонали АС и BD, О = АСCD.
3. ОКAD, К = ОКАВ.
4. ОК является искомым перпендикуляром.
Задание: окружность изображается эллипсом, требуется изобразить на чертеже пару взаимно перпендикулярных (то есть сопряженных) диаметров окружности.
1. Строим эллипс (с центром О). 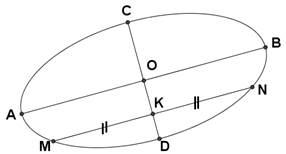
2. Проводим произвольный диаметр АВ.
3. Строим MNАВ.
4. Находим середину [ MN ]: МК = KN.
5. Проводим прямую ОК. Точки С и D – точки пересечения прямой ОК с эллипсом.
6. АВ и CD являются искомыми сопряженными диаметрами.
Задание: построить центр эллипса. 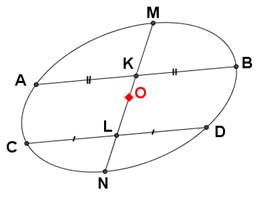
1. Строим эллипс (с центром О).
2. Проводим отрезок АВ.
3. Строим CDАВ.
4. Находим середину [ АВ ]: АК = КВ.
5. Находим середину [ CD ]: СL = LD.
6. Проводим прямую KL. Точки М и N – точки пересечения прямой с эллипсом.
7. Находим середину [ MN ]: NO = OM. О является искомым центром эллипса.