Операции сложения и умножения в 2-ной системе счисления.

Системы счисления.

Сист.счисления - это способ представления чисел и соответствующие ему правила действия над ними.

Знаки, используемые при записи чисел, называются цифрами.

С.с. можно разделить на непозиционные и позиционные.

В н.с.с. от положения цифры в записи числа не зависит величина, которую она обозначает (н-р., римские цифры).

В п.с.с. величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием п.с.с.

Позиционный характер легко понять на примере многозначного числа. Н-р., число 333: первая тройка- число сотен, вторая- десяток и третья- единицы.

Для записи в п.с.с. с основанием n нужно иметь алфавит из n цифр.

При n<10 используют n первых арабских цифр, при n>10 к десяти арабским цифрам добавляют буквы.

Алфавиты системы счисления.

Основание	Название	Алфавит
n=2 n=3 n=8 n=16	Двоичная Троичная Восьмеричная Шестнадцатеричная	0123456789ABCDEF

Пример записи числа с указанием основания системы, к которой число относится:

1011012, 36718, 3B8F16.

Позиция цифры в числе называется разрядом. Разряд числа вырастает справа налево от младших разрядов к старшим.

Число в п.с.с. записывается в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа.

В общем случае развернутой формой записи числа называют запись в виде:

Aq=+/-(a_n-1q^n-1+a_n-2q^n-2+…+a₀q⁰+a_-1q^-1+…+a_-mq^-m), где

A_q- само число;

q – основание с.с.;

a_i – цифры данной с.с.;

n – число разрядов целой части числа;

m – число разрядов дробной части числа.

Пример: развернутая запись числа 101,01.

101,01₂ = 1*2²+0*2¹+1*2⁰+0*2^-1+1*2^-2.

Пример. Двоичное число 101101₂ надо перевести в десятичную с.с.

Решение: над числом запишем степени основания двоичной системы, то есть степени двойки, затем получим развернутую запись числа, где q=2, n=6, m=0.

1⁵0⁴1³1²0¹1⁰=1*2⁵+0*2⁴+1*2³+1*2²+0*2¹+1*2⁰=32+8+4+1=45₁₀

Задача1. Перевести числа 1001₂, 11001₂, 10011₂, 11011₂, 11010₂ из двоичной с.с. в десятичную с.с.

Перевод десятичных чисел в другие системы счисления.

Для того, чтобы перевести целое число из 10-ой с.с. в 8,2 или 16-ную с.с., надо последовательно это число поделить на соответствующее основание системы. Деление продолжаем до тех пор, пока в частном не окажется число меньше, чем делитель. Затем записать полученный результат в «обратном порядке».

Пример. Десятичное число 215 надо перевести в 8-ную с.с. Для этого разделим число 215 на 8.

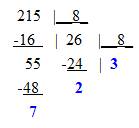
Ответ:327.

Теперь переведем число 215₁₀ в 16-ную с.с.

Здесь деление намного короче, но прежде, чем записать результат, надо вспомнить, что в 16-теричной системе нет символа 13. Этому значению соответствует символ D. Тогда результат запишется как D7, т.е. число 215₁₀=D7₁₆.

 

Аналогично получаем: 215₁₀=11010111₂

Задача2. Перевести числа 123, 58, и 317 из 10-ой в 2,8 и 16-ную с.с. Сделать проверку.

Перевод дробных чисел.

Пример1. Перевести десятичную дробь 0,25₁₀ в 2-ную с.с.

Для этого будем последовательно умножать на 2 дробную часть. При этом справа от черты записываем цифры дробной части, которые получаются в процессе умножения. Справа от вертикальной черты должно находиться столько же цифр, сколько их было в дробной части переводимого числа. Умножение проводим только с числом, стоящим СПРАВА от вертикальной черты. Умножаем до тех пор, пока не получим все нули справа и переход целой - влево. В качестве результата надо записать в дробную часть ответа цифры, оказавшиеся СЛЕВА от черты в порядке сверху вниз.

Пример2.

Получаем: 0,30A3D₁₆

Задача3. 0,1875₁₀, 0,4622₁₀, 0,7351₁₀ в 2-ную до 4-го знака после запятой. А также 0,18₁₀, 0,33₁₀ в 16-ную до 3 знака после запятой.

Задача4. Перевести из 10-ной в 2-ную с точностью до 4-го знака, число: 23,56.

Операции сложения и умножения в 2-ной системе счисления.

0+0=0 1+0=1 0+1=1 1+1=10

0*0=0 0*1=0 1*0=0 1*1=1

 

Пример. Найти сумму чисел 1010101₂ и 110111₂.

+

_______

Пример. Найти произведение чисел 11001₂ и 1101₂.

 

*

_____

+ 11001

_________

 

Логика высказываний.

Высказывание – это утверждение (предложение), о котором можно сказать, истинно оно или ложно.

Например, «Город Сочи расположен на берегу Черного моря» - истинно. «Город Ростов-на-Дону расположен на берегу Черного моря» - ложно.

Из простых высказываний можно образовать более сложные высказывания:

«А и В», «А или В», «неверно, что А», «если А, то В» («из А следует В»).

Зная истинность или ложность утверждений А,В можно установить истинность и ложность сложного высказывания.

Операции:

- конъюнкция , и

- дизъюнкция , или

- отрицание , не

- импликация

Пример. «Если будет дождь, мы не поедем в гости, будем сидеть дома»

А А - будет дождь, В – поедем в гости, С – будем сидеть дома.

Читается так: «из А следует не В и С».

Приоритеты операций:

существует договоренность о порядке выполнения логических операций, если этот порядок не размечен круглыми скобками. Наивысший приоритет имеют отрицание и скобки, затем конъюнкция, далее выполняется дизъюнкция и последней – импликация.

 

Таблица истинности:

X	Y	X Y	X Y	X Y	X

 

Другими словами:

конъюнкция истинна тогда и только тогда, когда оба операнда X и Y истинны;

дизъюнкция ложна тогда и только тогда, когда оба операнда X и Y ложны;

импликация ложна тогда и только тогда, когда первое высказывание истинно, а второе - ложно.